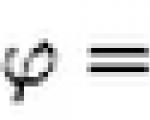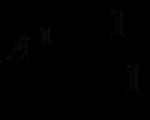x के साथ समीकरण हल करना। अपरिमेय समीकरण कैलकुलेटर ऑनलाइन

गणित हल करने के लिए. जल्दी ढूंढो गणित समीकरण समाधानमोड में ऑनलाइन. वेबसाइट www.site अनुमति देती है प्रश्न हल करेंलगभग कोई भी दिया गया बीजगणितीय, त्रिकोणमितीयया ट्रान्सेंडैंटल समीकरण ऑनलाइन. गणित के लगभग किसी भी अनुभाग का विभिन्न चरणों में अध्ययन करते समय, व्यक्ति को निर्णय लेना होता है समीकरण ऑनलाइन. तुरंत उत्तर पाने के लिए, और सबसे महत्वपूर्ण रूप से सटीक उत्तर पाने के लिए, आपको एक ऐसे संसाधन की आवश्यकता है जो आपको ऐसा करने की अनुमति दे। www.site को धन्यवाद समीकरणों को ऑनलाइन हल करेंकुछ मिनट लगेंगे. गणितीय हल करते समय www.site का मुख्य लाभ समीकरण ऑनलाइन- जारी प्रतिक्रिया की गति और सटीकता है. साइट किसी का भी समाधान करने में सक्षम है बीजगणितीय समीकरण ऑनलाइन, त्रिकोणमितीय समीकरण ऑनलाइन, ट्रान्सेंडैंटल समीकरण ऑनलाइन, और समीकरणमोड में अज्ञात पैरामीटर के साथ ऑनलाइन. समीकरणएक शक्तिशाली गणितीय उपकरण के रूप में कार्य करें समाधानव्यावहारिक कार्य. मदद से गणितीय समीकरणउन तथ्यों और संबंधों को व्यक्त करना संभव है जो पहली नज़र में भ्रमित करने वाले और जटिल लग सकते हैं। अज्ञात मात्राएँ समीकरणसमस्या को सूत्रबद्ध करके पाया जा सकता है गणितीयरूप में भाषा समीकरणऔर तय करनामोड में प्राप्त कार्य ऑनलाइनवेबसाइट www.site पर। कोई बीजगणितीय समीकरण, त्रिकोणमितीय समीकरणया समीकरणयुक्त ट्रान्सेंडैंटलआपको आसानी से सुविधाएँ देता है तय करनाऑनलाइन और सही उत्तर प्राप्त करें। प्राकृतिक विज्ञान का अध्ययन करते समय व्यक्ति को अनिवार्य रूप से आवश्यकता का सामना करना पड़ता है समीकरण हल करना. इस मामले में, उत्तर सटीक होना चाहिए और इसे तुरंत मोड में प्राप्त किया जाना चाहिए ऑनलाइन. इसलिए, के लिए गणित के समीकरण ऑनलाइन हल करेंहम साइट www.site की अनुशंसा करते हैं, जो आपके लिए अपरिहार्य कैलकुलेटर बन जाएगी बीजगणितीय समीकरणों को ऑनलाइन हल करें, त्रिकोणमितीय समीकरण ऑनलाइन, और ट्रान्सेंडैंटल समीकरण ऑनलाइनया समीकरणअज्ञात मापदंडों के साथ. विभिन्न की जड़ों को खोजने की व्यावहारिक समस्याओं के लिए गणितीय समीकरणसंसाधन www.. समाधान समीकरण ऑनलाइनस्वयं, प्राप्त उत्तर की जाँच करना उपयोगी है समीकरणों का ऑनलाइन समाधानवेबसाइट www.site पर। समीकरण को सही ढंग से लिखना और तुरंत प्राप्त करना आवश्यक है ऑनलाइन समाधान, जिसके बाद यह केवल समीकरण के आपके समाधान के साथ उत्तर की तुलना करने के लिए रह जाता है। उत्तर जांचने में एक मिनट से ज्यादा नहीं लगेगा, काफी है समीकरण को ऑनलाइन हल करेंऔर उत्तरों की तुलना करें. इससे आपको गलतियों से बचने में मदद मिलेगी फ़ैसलाऔर समय रहते उत्तर सही करें समीकरणों को ऑनलाइन हल करनादोनों में से एक बीजगणितीय, त्रिकोणमितीय, उत्कृष्टया समीकरणअज्ञात मापदंडों के साथ.

सेवा असाइनमेंट. मैट्रिक्स कैलकुलेटर को रैखिक समीकरणों की प्रणालियों को मैट्रिक्स तरीके से हल करने के लिए डिज़ाइन किया गया है (समान समस्याओं को हल करने का एक उदाहरण देखें)।

अनुदेश. ऑनलाइन समाधान के लिए, आपको समीकरण के प्रकार का चयन करना होगा और संबंधित आव्यूहों का आयाम निर्धारित करना होगा। जहां ए, बी, सी को मैट्रिक्स दिया गया है, एक्स वांछित मैट्रिक्स है। फॉर्म (1), (2) और (3) के मैट्रिक्स समीकरणों को व्युत्क्रम मैट्रिक्स ए -1 के माध्यम से हल किया जाता है। यदि व्यंजक A यदि अभिव्यक्ति A*X = B 2 दी गई है, तो मैट्रिक्स B को पहले वर्गित किया जाना चाहिए।

मैट्रिसेस पर बुनियादी संचालन से खुद को परिचित करने की भी सिफारिश की जाती है।

उदाहरण 1। व्यायाम. मैट्रिक्स समीकरण का हल खोजें
समाधान. निरूपित करें:
फिर मैट्रिक्स समीकरण इस रूप में लिखा जाएगा: A·X·B = C.
मैट्रिक्स A का निर्धारक detA=-1 है
चूँकि A एक गैर-एकवचन मैट्रिक्स है, इसलिए एक व्युत्क्रम मैट्रिक्स A -1 है। बायीं ओर के समीकरण के दोनों पक्षों को A -1 से गुणा करें: इस समीकरण के बायीं ओर के दोनों पक्षों को A -1 से और दायीं ओर के दोनों पक्षों को B -1 से गुणा करें: A -1 A X B B -1 = A -1 C B -1। चूँकि A A -1 = B B -1 = E और E X = X E = X, तो X = A -1 C B -1

उलटा मैट्रिक्स ए -1:
व्युत्क्रम मैट्रिक्स B -1 ज्ञात कीजिए।
ट्रांसपोज़ मैट्रिक्स बी टी:
उलटा मैट्रिक्स बी -1:
हम सूत्र द्वारा मैट्रिक्स एक्स की तलाश कर रहे हैं: एक्स = ए -1 सी बी -1

उत्तर:

उदाहरण #2. व्यायाम।मैट्रिक्स समीकरण हल करें
समाधान. निरूपित करें:
फिर मैट्रिक्स समीकरण इस रूप में लिखा जाएगा: A X = B.
मैट्रिक्स A का निर्धारक detA=0 है
चूँकि A एक पतित मैट्रिक्स है (निर्धारक 0 है), इसलिए, समीकरण का कोई हल नहीं है।

उदाहरण #3. व्यायाम। मैट्रिक्स समीकरण का हल खोजें
समाधान. निरूपित करें:
फिर मैट्रिक्स समीकरण इस रूप में लिखा जाएगा: X·A = B.
मैट्रिक्स A का निर्धारक detA=-60 है
चूँकि A एक गैर-एकवचन मैट्रिक्स है, इसलिए एक व्युत्क्रम मैट्रिक्स A -1 है। समीकरण के दाहिनी ओर दोनों पक्षों को A -1 से गुणा करें: X A A -1 = B A -1, जिससे हमें पता चलता है कि X = B A -1
व्युत्क्रम मैट्रिक्स A -1 खोजें।
ट्रांसपोज़्ड मैट्रिक्स ए टी:
उलटा मैट्रिक्स ए -1:
हम सूत्र द्वारा मैट्रिक्स एक्स की तलाश कर रहे हैं: एक्स = बी ए -1


उत्तर: >

द्विघात समीकरणों का अध्ययन कक्षा 8 में किया जाता है, इसलिए यहाँ कुछ भी जटिल नहीं है। उन्हें हल करने की क्षमता जरूरी है.

द्विघात समीकरण ax 2 + bx + c = 0 के रूप का एक समीकरण है, जहां गुणांक a, b और c मनमानी संख्याएं हैं, और a ≠ 0 है।

विशिष्ट समाधान विधियों का अध्ययन करने से पहले, हम ध्यान दें कि सभी द्विघात समीकरणों को तीन वर्गों में विभाजित किया जा सकता है:

1. कोई जड़ नहीं है;
2. उनकी बिल्कुल एक ही जड़ है;
3. उनकी दो अलग-अलग जड़ें हैं।

यह द्विघात और रैखिक समीकरणों के बीच एक महत्वपूर्ण अंतर है, जहां मूल हमेशा मौजूद होता है और अद्वितीय होता है। यह कैसे निर्धारित करें कि किसी समीकरण के कितने मूल हैं? इसके लिए एक अद्भुत बात है - विभेदक.

विभेदक

मान लीजिए कि द्विघात समीकरण ax 2 + bx + c = 0 दिया गया है। तब विभेदक केवल संख्या D = b 2 − 4ac है।

यह सूत्र कंठस्थ होना चाहिए। यह कहां से आता है यह अब महत्वपूर्ण नहीं है. एक और बात महत्वपूर्ण है: विवेचक के चिह्न से, आप यह निर्धारित कर सकते हैं कि एक द्विघात समीकरण की कितनी जड़ें हैं। अर्थात्:

1. यदि डी< 0, корней нет;
2. यदि D = 0, तो वास्तव में एक ही मूल है;
3. यदि D > 0, तो दो जड़ें होंगी।

कृपया ध्यान दें: विवेचक जड़ों की संख्या को इंगित करता है, न कि उनके संकेतों को, जैसा कि किसी कारण से कई लोग सोचते हैं। उदाहरणों पर एक नज़र डालें और आप स्वयं सब कुछ समझ जाएंगे:

काम। द्विघात समीकरण के कितने मूल होते हैं:

1. एक्स 2 - 8एक्स + 12 = 0;
2. 5x2 + 3x + 7 = 0;
3. x2 − 6x + 9 = 0.

हम पहले समीकरण के लिए गुणांक लिखते हैं और विवेचक ढूंढते हैं:
ए = 1, बी = −8, सी = 12;
डी = (−8) 2 − 4 1 12 = 64 − 48 = 16

इसलिए, विवेचक सकारात्मक है, इसलिए समीकरण के दो अलग-अलग मूल हैं। हम दूसरे समीकरण का भी इसी प्रकार विश्लेषण करते हैं:
ए = 5; बी = 3; सी = 7;
डी = 3 2 - 4 5 7 = 9 - 140 = -131।

विवेचक नकारात्मक है, कोई जड़ें नहीं हैं। अंतिम समीकरण बना हुआ है:
ए = 1; बी = -6; सी = 9;
डी = (−6) 2 − 4 1 9 = 36 − 36 = 0.

विवेचक शून्य के बराबर है - मूल एक होगा।

ध्यान दें कि प्रत्येक समीकरण के लिए गुणांक लिखे गए हैं। हाँ, यह लंबा है, हाँ, यह थकाऊ है - लेकिन आप बाधाओं को मिश्रित नहीं करेंगे और मूर्खतापूर्ण गलतियाँ नहीं करेंगे। अपने लिए चुनें: गति या गुणवत्ता।

वैसे, यदि आप "अपना हाथ भरते हैं", तो थोड़ी देर बाद आपको सभी गुणांक लिखने की आवश्यकता नहीं होगी। आप अपने दिमाग में ऐसे ऑपरेशन करेंगे। अधिकांश लोग 50-70 समीकरणों को हल करने के बाद कहीं न कहीं ऐसा करना शुरू करते हैं - सामान्य तौर पर, इतना नहीं।

द्विघात समीकरण की जड़ें

अब चलिए समाधान की ओर बढ़ते हैं। यदि विवेचक D > 0 है, तो मूल सूत्रों का उपयोग करके पाया जा सकता है:

द्विघात समीकरण के मूलों का मूल सूत्र

जब D = 0, आप इनमें से किसी भी सूत्र का उपयोग कर सकते हैं - आपको वही संख्या मिलेगी, जो उत्तर होगी। अंततः, यदि डी< 0, корней нет — ничего считать не надо.

1. एक्स 2 - 2एक्स - 3 = 0;
2. 15 - 2x - x2 = 0;
3. x2 + 12x + 36 = 0.

पहला समीकरण:
x 2 - 2x - 3 = 0 ⇒ ए = 1; बी = −2; सी = -3;
डी = (−2) 2 − 4 1 (−3) = 16.

D > 0 ⇒ समीकरण के दो मूल हैं। आइए उन्हें खोजें:

दूसरा समीकरण:
15 − 2x − x 2 = 0 ⇒ a = −1; बी = −2; सी = 15;
डी = (−2) 2 − 4 (−1) 15 = 64.

D > 0 ⇒ समीकरण के फिर से दो मूल हैं। आइए उन्हें खोजें

\[\begin(संरेखित करें) और ((x)_(1))=\frac(2+\sqrt(64))(2\cdot \left(-1 \right))=-5; \\ & ((x)_(2))=\frac(2-\sqrt(64))(2\cdot \left(-1 \right))=3. \\ \end(संरेखित करें)\]

अंत में, तीसरा समीकरण:
x 2 + 12x + 36 = 0 ⇒ ए = 1; बी = 12; सी = 36;
डी = 12 2 − 4 1 36 = 0.

D = 0 ⇒ समीकरण का एक मूल है। कोई भी फार्मूला इस्तेमाल किया जा सकता है. उदाहरण के लिए, पहला:

जैसा कि आप उदाहरणों से देख सकते हैं, सब कुछ बहुत सरल है। यदि आप सूत्र जानते हैं और गिनने में सक्षम हैं, तो कोई समस्या नहीं होगी। अक्सर, त्रुटियां तब होती हैं जब सूत्र में ऋणात्मक गुणांक प्रतिस्थापित कर दिए जाते हैं। यहां, फिर से, ऊपर वर्णित तकनीक मदद करेगी: सूत्र को शाब्दिक रूप से देखें, प्रत्येक चरण को चित्रित करें - और बहुत जल्द गलतियों से छुटकारा पाएं।

अपूर्ण द्विघात समीकरण

ऐसा होता है कि द्विघात समीकरण परिभाषा में दिए गए समीकरण से कुछ भिन्न होता है। उदाहरण के लिए:

1. x2 + 9x = 0;
2. x2 − 16 = 0.

यह देखना आसान है कि इन समीकरणों में से एक पद गायब है। ऐसे द्विघात समीकरणों को मानक समीकरणों की तुलना में हल करना और भी आसान होता है: उन्हें विवेचक की गणना करने की भी आवश्यकता नहीं होती है। तो आइए एक नई अवधारणा का परिचय दें:

समीकरण ax 2 + bx + c = 0 को अपूर्ण द्विघात समीकरण कहा जाता है यदि b = 0 या c = 0, अर्थात। चर x या मुक्त तत्व का गुणांक शून्य के बराबर है।

बेशक, एक बहुत ही कठिन मामला संभव है जब ये दोनों गुणांक शून्य के बराबर हों: b \u003d c \u003d 0. इस मामले में, समीकरण ax 2 \u003d 0 का रूप लेता है। जाहिर है, ऐसे समीकरण में एक एकल होता है रूट: x \u003d 0.

आइए अन्य मामलों पर विचार करें। मान लीजिए b = 0, तो हमें ax 2 + c = 0 के रूप का एक अधूरा द्विघात समीकरण मिलता है। आइए इसे थोड़ा रूपांतरित करें:

चूँकि अंकगणितीय वर्गमूल केवल एक गैर-ऋणात्मक संख्या से मौजूद होता है, अंतिम समानता केवल तभी समझ में आती है जब (−c / a ) ≥ 0. निष्कर्ष:

1. यदि ax 2 + c = 0 के रूप का अपूर्ण द्विघात समीकरण असमानता (−c / a ) ≥ 0 को संतुष्ट करता है, तो दो जड़ें होंगी। सूत्र ऊपर दिया गया है;
2. यदि (−c / a )< 0, корней нет.

जैसा कि आप देख सकते हैं, विवेचक की आवश्यकता नहीं थी - अपूर्ण द्विघात समीकरणों में कोई जटिल गणना नहीं होती है। वास्तव में, असमानता (−c / a ) ≥ 0 को याद रखना भी आवश्यक नहीं है। यह x 2 के मान को व्यक्त करने और यह देखने के लिए पर्याप्त है कि समान चिह्न के दूसरी तरफ क्या है। यदि कोई धनात्मक संख्या है, तो दो जड़ें होंगी। यदि नकारात्मक है, तो कोई जड़ें नहीं होंगी।

अब आइए ax 2 + bx = 0 के रूप के समीकरणों से निपटें, जिसमें मुक्त तत्व शून्य के बराबर है। यहां सब कुछ सरल है: हमेशा दो जड़ें होंगी। यह बहुपद का गुणनखंड करने के लिए पर्याप्त है:

सामान्य गुणनखंड को कोष्ठक से बाहर निकालना

जब कम से कम एक कारक शून्य के बराबर हो तो उत्पाद शून्य के बराबर होता है। यहीं से जड़ें आती हैं। अंत में, हम इनमें से कई समीकरणों का विश्लेषण करेंगे:

काम। द्विघात समीकरण हल करें:

1. x2 − 7x = 0;
2. 5x2 + 30 = 0;
3. 4x2 − 9 = 0.

x 2 − 7x = 0 ⇒ x (x − 7) = 0 ⇒ x 1 = 0; x2 = −(−7)/1 = 7.

5x2 + 30 = 0 ⇒ 5x2 = -30 ⇒ x2 = -6. कोई जड़ें नहीं हैं, क्योंकि वर्ग ऋणात्मक संख्या के बराबर नहीं हो सकता.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1.5; x 2 = -1.5.