Hem › Kropp › Diophantusprojektet och dess upptäckter. Sammanfattning: Diophantus

Diophantusprojektet och dess upptäckter. Sammanfattning: Diophantus

Koefficienter vars lösningar måste hittas bland heltal.

Diophantus av Alexandria
Διόφαντος ὁ Ἀλεξανδρεύς

Födelsedatum	inte tidigare och inte senare eller
Födelseort	Alexandria, Egypten
Dödsdatum	inte tidigare och inte senare
Ett land	Antika Rom
Vetenskapligt område	talteori
Känd som	"algebras far"
Diophantus av Alexandria på Wikimedia Commons

Biografi

Nästan ingenting är känt om detaljerna i hans liv. Å ena sidan citerar Diophantus Hypsicles (2:a århundradet f.Kr.); å andra sidan skriver Theon av Alexandria (ca 350 e.Kr.) om Diophantus, varav vi kan dra slutsatsen att hans liv utspelade sig inom denna periods gränser. Ett möjligt förtydligande av Diophantus livstid bygger på det faktum att han Aritmetisk tillägnad "den mest ärevördiga Dionysius". Man tror att denne Dionysius är ingen mindre än biskop Dionysius av Alexandria, som levde i mitten av 300-talet. n. e.

Det motsvarar att lösa följande ekvation:

x = x 6 + x 12 + x 7 + 5 + x 2 + 4 (\displaystyle x=(\frac (x)(6))+(\frac (x)(12))+(\frac (x) (7))+5+(\frac (x)(2))+4)

Denna ekvation ger x = 84 (\displaystyle x=84), det vill säga åldern för Diophantus är lika med 84 år. Däremot kan riktigheten av informationen inte bekräftas.

Aritmetisk Diophanta

Diophantus huvudverk - Aritmetisk i 13 böcker. Tyvärr har bara 6 (eller 10, se nedan) av de första 13 böckerna överlevt.

Den första boken föregås av en omfattande introduktion, som beskriver den notation som Diophantus använder. Diophantus kallar det okända "numret" ( ἀριθμός ) och betecknas med bokstaven ς , ruta okänd - symbol Δ Υ (Förkortning av δύναμις - "grad"), kuben för det okända - symbol Κ Υ (Förkortning av κύβος - "kub"). Särskilda tecken finns för följande grader av det okända, upp till den sjätte, kallad kub-kub, och för deras motsatta grader, upp till minus den sjätte.

Diophantus har inget additionstecken: han skriver helt enkelt positiva termer bredvid varandra i fallande gradordning, och i varje term skrivs först graden av det okända och sedan den numeriska koefficienten. De subtraherade termerna skrivs också sida vid sida, och ett speciellt tecken i form av en inverterad bokstav Ψ placeras framför hela gruppen. Likhetstecknet representeras av två bokstäver ἴσ (Förkortning av ἴσος - "likvärdig").

En regel för att ta med liknande termer och en regel för att addera eller subtrahera samma tal eller uttryck på båda sidor av en ekvation formulerades: vad al-Khorezmi senare började kalla "algebra och almukabala." Teckenregeln har införts: "minus med plus ger minus", "minus för minus ger plus"; Denna regel används när man multiplicerar två uttryck med subtraherade termer. Allt detta är formulerat i allmänna termer, utan hänvisning till geometriska tolkningar.

Det mesta av arbetet är en samling problem med lösningar (det finns totalt 189 i de sex bevarade böckerna, tillsammans med de fyra från den arabiska delen - 290), skickligt utvalda för att illustrera allmänna metoder. Huvud problem Aritmetisk- hitta positiva rationella lösningar på osäkra ekvationer. Rationella tal behandlas av Diophantus på samma sätt som naturliga tal, vilket inte är typiskt för forntida matematiker.

Först undersöker Diophantus system av andra ordningens ekvationer i två okända; den specificerar en metod för att hitta andra lösningar om en redan är känd. Sedan tillämpar han liknande metoder på ekvationer av högre grader. Bok VI undersöker problem relaterade till räta trianglar med rationella sidor.

Inflytande Aritmetisk för matematikens utveckling

På 900-talet Aritmetisköversattes till arabiska (se Kusta ibn Luka), varefter matematiker från islamiska länder (Abu Kamil och andra) fortsatte en del av Diophantus forskning. I Europa, intresse för Aritmetiskökade efter att Raphael Bombelli översatte och publicerade detta verk till latin och publicerade 143 problem från det i sin Algebra(1572). År 1621 kom en klassisk, grundligt kommenterad latinsk översättning Aritmetisk, avrättad av Bachet de Meziriac.

Diophantus metoder påverkade i hög grad François Viète och Pierre Fermat; men i modern tid löses obestämda ekvationer vanligtvis i heltal och inte i rationella tal, som Diophantus gjorde. När Pierre Fermat läste Diophantus aritmetik, redigerad av Bachet de Mezyriac, kom han till slutsatsen att en av ekvationerna som liknar de som Diophantus betraktade inte hade några lösningar i heltal, och noterade i marginalen att han hade hittat "ett verkligt underbart bevis på detta teorem ... bokens marginaler är dock för smala för att inkludera den." Detta uttalande är nu känt som Fermats sista sats.

På 1900-talet upptäcktes den arabiska texten i ytterligare fyra böcker under namnet Diophantus. Aritmetisk. I. G. Bashmakova och E. I. Slavutin, efter att ha analyserat denna text, lade fram en hypotes att dess författare inte var Diophantus, utan en kommentator som var väl insatt i Diophantus metoder, troligen Hypatia. Den betydande luckan i metodiken för att lösa problem i de första tre och sista tre böckerna fylls dock väl av fyra böcker med arabisk översättning. Detta tvingar oss att ompröva resultaten från tidigare studier. . [ ]

Andra verk av Diophantus

Avhandling av Diophantus Om polygonala tal (Περὶ πολυγώνων ἀριθμῶν ) inte helt bevarad; i den bevarade delen härleds ett antal hjälpsatser med geometriska algebrametoder.

Från Diophantus verk Om att mäta ytor (ἐπιπεδομετρικά ) Och Om multiplikation (Περὶ πολλαπλασιασμοῦ ) har också bara fragment överlevt.

Diophantus bok Porismer känd endast från ett fåtal satser som används i Aritmetisk.

se även

Samling Budé" (2 volymer publicerade: böckerna 4 - 7).

Forskning:

Bashmakova I. G., Slavutin E. I., Rosenfeld B.A. Arabisk version av "Aritmetik" av Diophantus // Historiska och matematiska studier. - M., 1978. - Utgåva. XXIII. - S. 192 - 225.
Bashmakova I. G. Aritmetik av algebraiska kurvor: (Från Diophantus till Poincaré) // Historiska och matematiska studier. - 1975. - Utgåva. 20. - s. 104 - 124.
Bashmakova I. G. Diophantus och Diophantine ekvationer. - M.: Nauka, 1972 (Reprint: M.: LKI, 2007). Per. På honom. språk: Diophant und diophantische Gleichungen. - Basel; Stuttgart: Birkhauser, 1974. Trans. på engelska. språk: Diophantus och Diophantine Ekvationer/ Övers. av A. Shenitzer med redaktionell hjälp av H. Grant och uppdaterad av J. Silverman // The Dolciani Mathematical Expositions. - Nr 20. - Washington, DC: Mathematical Association of America, 1997.
Bashmakova I. G. Diophantus och Fermat: (Om historien om metoden för tangenter och extrema) // Historiska och matematiska studier. - M., 1967. - Utgåva. VII. - S. 185 - 204.
Bashmakova I. G., Slavutin E. I. Historia om Diophantine analys från Diophantus till Fermat. - M.: Nauka, 1984.
Matematikens historia från antiken till början av 1800-talet. - T. I: Från de äldsta. gånger före början av New Age. tid / Ed. A. P. Jusjkevitj. - M., Nauka, 1970.
Slavutin E.I. Diophantus’ algebra och dess ursprung // Historiska och matematiska studier. - M., 1975. - Utgåva. 20. - s. 63 - 103.
Shchetnikov A.I. Kan Diophantus från Alexandrias bok "Om polygonala tal" kallas rent algebraisk? // Historisk och matematisk forskning. - M., 2003. - Utgåva. 8 (43). - s. 267 - 277.
Heath Th. L. Diophantus av Alexandria, A Study in the History of Greek Algebra. - Cambridge, 1910 (Repr.: NY, 1964).
Knorr W.R. Arithmktikê stoicheiôsis: Om Diophantus och hjälten från Alexandria // Historia Mathematica. - 20. - 1993. - S. 180 - 192.
Christianidis J. Diophantus väg: Några förtydliganden om Diophantus lösningsmetod // Historia Mathematica. - 34. - 2007. - S. 289 - 305.
Rashed R., Houzel C. Les Arithmétiques de Diophante. Lecture historique et mathématique . - De Gruyter, 2013.

Kommunal läroanstalt

"Lyceum nr 10" Perm

Diophantus. Diofantiska ekvationer

Klart jobbet

Ilyina Yana,

Elev i 11:e klass

Handledare

Zolotukhina L. V.

matematiklärare

Perm, 2010

Inledning……………………………………………………………………………………………….3

1. Diophantus………………………………………………………………………………………..…4

2. Siffror och symboler………………………………………………………………6

3. Diofantisk ekvation…………………………………………………..…8

4. Lösningar………………………………………………………………..12

Slutsats………………………………………………………………………………………………15

Referenser………………………………………………………………16

Introduktion

Dagens skolbarn löser olika ekvationer. I del C av Unified State Examination-uppgifterna finns en intressant ekvation som kallas den diofantiska ekvationen. I sina verk ställde Diophantus inte bara problemet med att lösa obestämda ekvationer i rationella tal, utan gav också några allmänna metoder för att lösa dem. Dessa metoder kommer att vara mycket användbara för dagens elfteklassare som ska göra matteprovet.

Diophantus gjorde ett lika stort bidrag till utvecklingen av matematiken som Arkimedes. Detta är vad Arkimedes till exempel gjorde: när han bestämde areorna för en ellips, ett segment av en parabel, ytan på en sfär, volymerna av en sfär och andra kroppar, använde han metoden för integralsummor och metoden för passage till gränsen, men ingenstans gav han en allmän abstrakt beskrivning av dessa metoder. Forskare från 1500- och 1600-talen var tvungna att noggrant studera och omorganisera hans verk på ett nytt sätt för att isolera Arkimedes metoder därifrån. Situationen är liknande med Diophantus. Hans metoder förstods och tillämpades på nya problem av Viethe och Fermat, d.v.s. samtidigt som Arkimedes löstes.

1. Diophantus

Diophantus presenterar ett av de svåraste mysterierna i vetenskapens historia. Vi vet inte när han levde, inte heller hans föregångare som skulle ha arbetat inom samma område. Hans verk är som en gnistrande eld mitt i fullständigt ogenomträngligt mörker. Tidsperioden när Diophantus kunde ha levt är ett halvt årtusende! Den nedre gränsen för detta intervall bestäms utan svårighet: i sin bok om polygonala tal nämner Diophantus upprepade gånger matematikern Hypsicles of Alexandria, som levde i mitten av 200-talet f.Kr. e. Å andra sidan, i kommentarerna från Theon av Alexandria till "Almagest" av den berömda astronomen Ptolemaios, placeras ett utdrag ur Diophantus verk. Theon levde i mitten av 300-talet e.Kr. e. Detta bestämmer den övre gränsen för detta intervall. Alltså, 500 år!

Men platsen för Diophantus är välkänd - det här är det berömda Alexandria, centrum för den hellenistiska världens vetenskapliga tanke.

För att uttömma allt som är känt om Diophantus personlighet presenterar vi en gåtadikt som har kommit ner till oss:

Diophantus aska vilar i graven; förundras över henne - och stenen
Den avlidnes ålder kommer att tala genom hans kloka konst.
Enligt gudarnas vilja levde han en sjättedel av sitt liv som barn.
Och jag mötte halv sex med ludd på kinderna.
Det var bara den sjunde dagen när han förlovade sig med sin flickvän.
Efter att ha tillbringat fem år med henne, väntade vismannen på sin son;
Hans fars älskade son levde bara halva sitt liv.
Han togs från sin far vid sin tidiga grav.
Två gånger två år sörjde föräldern en tung sorg,
Här såg jag gränsen för mitt sorgliga liv.

Härifrån är det lätt att räkna ut att Diophantus levde 84 år. Men för detta behöver du inte behärska Diophantus konst! Det räcker för att kunna lösa en ekvation av 1:a graden med en okänd, och egyptiska skriftlärda kunde göra detta 2 tusen år f.Kr. e.

Men det mest mystiska är Diophantus verk. Sex böcker av 13 har nått oss, som slogs samman till "Aritmetik". Stilen och innehållet i dessa böcker skiljer sig kraftigt från klassiska antika verk om talteori och algebra, exempel på vilka vi känner från Euklids element, hans data och lemman från Arkimedes och Apollonius verk. "Aritmetik" var utan tvekan resultatet av många studier som förblev helt okända för oss. Vi kan bara gissa om dess rötter och förundras över rikedomen och skönheten i dess metoder och resultat.

"Aritmetik" av Diophantus är en samling problem (det finns totalt 189), som var och en är utrustad med en lösning (eller flera lösningsmetoder) och nödvändiga förklaringar. Därför verkar det vid första anblicken inte vara ett teoretiskt verk. En noggrann läsning visar dock att problemen är noggrant utvalda och tjänar till att illustrera mycket specifika, strikt genomtänkta metoder. Som brukligt var i forna tider formuleras metoder inte i allmän form, utan upprepas för att lösa liknande problem.

2. Siffror och symboler

Diophantus börjar med grundläggande definitioner och en beskrivning av bokstavssymbolerna han kommer att använda.

I klassisk grekisk matematik, som fann sin fullbordan i Euklids element, under numret άριJμός - " arytmi" eller " aritmos"; därav namnet "aritmetik" för vetenskapen om tal) uppfattades som en uppsättning enheter, dvs. heltal. Varken bråk eller irrationalitet kallades siffror. Strängt taget finns det inga fraktioner i Principia. Enheten anses vara odelbar och istället för bråkdelar av en enhet betraktas förhållanden mellan heltal; irrationaliteter uppträder som förhållanden av inkommensurabla segment, till exempel var talet vi nu betecknar √2 för de klassiska grekerna förhållandet mellan diagonalen av en kvadrat till dess sida. Det var inget tal om negativa siffror. Det fanns inte ens några motsvarigheter för dem. Vi finner en helt annan bild hos Diophantus.

Diophantus ger den traditionella definitionen av tal som en uppsättning enheter, men söker senare efter sina problem positiv rationell lösningar och kallar varje sådan lösning ett nummer (άριJμός - " arytmi »).

Men saken stannar inte där. Diophantus introducerar negativa tal: han kallar dem specialtermen λει̃ψις - " leipsis" - härlett från verbet λει̃πω - " leipo”, vilket betyder att sakna, att sakna, så att själva termen skulle kunna översättas med ordet ”brist”. Det är förresten vad den berömda ryske vetenskapshistorikern I. Timchenko gör. Diophantus kallar ett positivt tal ordet ΰπαρξις - " iparxis”, som betyder existens, vara, och i plural kan detta ord betyda egendom eller egendom. Diophantus terminologi för relativa tal ligger alltså nära den som användes under medeltiden i öst och Europa. Troligtvis var det helt enkelt en översättning från grekiska till arabiska, sanskrit, latin och sedan till olika språk i Europa.

Observera att termen λει̃ψις är " leipsis" - kan inte översättas som "subtraherad", som många översättare av Diophantus gör, eftersom Diophantus för subtraktionens funktion använder helt andra termer, nämligen άφελει̃ν - " afelein"eller άφαιρει̃ν -" avirrain", som härrör från verbet άφαιρεω - " afireo"- hämtmat. När man transformerar ekvationer använder Diophantus själv ofta standarduttrycket "lägg till λει̃ψις på båda sidor."

Vi har uppehållit oss så detaljerat vid den filologiska analysen av Diophantus text för att övertyga läsaren om att vi inte kommer att avvika från sanningen om vi översätter Diophantus termer som "positiva" och "negativa".

Diophantus formulerar teckenregeln för relativa tal:

"ett negativt multiplicerat med ett negativt ger ett positivt, medan ett negativt multiplicerat med ett positivt ger ett negativt, och det särskiljande tecknet för ett negativt är en inverterad och förkortad (bokstav) ψ."

”Efter att jag förklarat multiplikation för dig blir divisionen av de föreslagna termerna också tydlig; Nu blir det bra att börja öva på addition, subtraktion och multiplikation av sådana termer. Lägg till positiva och negativa termer med olika koefficienter till andra termer som antingen är positiva eller lika positiva och negativa, och subtrahera andra positiva och lika positiva och negativa termer från positiva och andra negativa termer."

Observera att även om Diophantus bara söker rationella positiva lösningar, använder han i mellanberäkningar villigt negativa tal.

Vi kan alltså notera att Diophantus utökade talfältet till ett fält av rationella tal där alla fyra aritmetikens operationer kan utföras utan hinder.

3. Diofantisk ekvation

Definition - algebraiska ekvationer eller system av algebraiska ekvationer med heltalskoefficienter, med ett antal okända som överstiger antalet ekvationer och för vilka heltalslösningar eller rationella lösningar söks.

yxa + förbi = 1

Var A Och b- coprime heltal

Samprimtal flera heltal så att de gemensamma divisorerna för alla dessa tal bara är + 1 och - 1. Den minsta multipeln av ett par primtal är lika med deras produkt.

har oändligt många lösningar:

Om x0 Och y0- en lösning, sedan siffrorna

X = x0 + miljarder

på = y0 -en

(n- vilket heltal som helst) kommer också att vara lösningar.

Ett annat exempel på D. u.

x2 + y2 = z2

Positiva heltalslösningar till denna ekvation representerar längden på benen X , på och hypotenusa z räta trianglar med heltals sidlängder kallas pytagoreiska tal.

trippel av naturliga tal så att en triangel vars sidolängder är proportionella (eller lika) med dessa tal är rektangulär.

Alla tripletter av coprime Pythagoras tal kan erhållas med hjälp av formlerna

X = m2 - n2

på = 2mn

z = m2 + n2

Var m Och n- heltal ( m > n > 0).

Denna ekvation definierar på planet R 2 algebraisk kurvaΓ. Vi kommer att kalla den rationella lösningen (2) rationell poäng kurva Γ. I det följande kommer vi ofta att tillgripa geometrins språk, även om Diophantus själv inte använder det någonstans. Men geometriskt språk har nu blivit en så integrerad del av det matematiska tänkandet att många fakta blir lättare att förstå och förklara med dess hjälp.

Först och främst är det nödvändigt att ge någon klassificering av ekvationerna (2) eller, vilket är samma, algebraiska kurvor. Det naturligaste och tidigaste att uppstå är deras klassificering efter ordning.

Låt oss påminna dig om det i ordning kurva (2) är den maximala ordningen för termerna för polynomet f (x , y), där ordningen för en term förstås som summan av potenser vid x Och y. Den geometriska innebörden av detta koncept är att en rät linje skär en ordningskurva n exakt kl n poäng. När man räknar punkter måste man naturligtvis ta hänsyn till mångfalden av skärningspunkter, såväl som komplexa och "oändligt avlägsna" punkter. Så till exempel en cirkel x 2 + y 2 = 1 och rak x + y= 2 skär i två komplexa punkter, och hyperbeln x 2 – y 2 = 1 och rak y =x- vid två punkter i oändligheten, samma hyperbel med en rak linje x=1 har en gemensam multiplicitetspunkt 2.

Dock för ändamålen diopantin analys(det här namnet gavs till området matematik som växte fram ur problemen med att lösa obestämda ekvationer, men nu kallas det oftare för diofantisk geometri) klassificering efter ordning visade sig vara för grov.

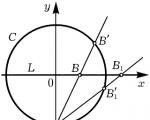
Ris. 1.

Låt oss förklara detta med ett exempel. Låt en cirkel ges C : x 2 + y 2 = 1 och vilken rät linje som helst med rationella koefficienter, till exempel, L : y=0. Låt oss visa att de rationella punkterna i denna cirkel och linjen kan sättas i en en-till-en-korrespondens. Detta kan till exempel göras så här: fixa punkten A(0,–1) cirklar och tilldela varje rationell punkt B hetero L punkt B" cirkel C, liggande i korsningen C och rak AB(Figur 1). Att punktens koordinater B" kommer att vara rationell, kommer vi att låta läsaren bevisa det själv eller läsa ett liknande bevis från Diophantus (det kommer att presenteras i nästa stycke). Uppenbarligen kan samma överensstämmelse upprättas mellan de rationella punkterna för varje konisk sektion, om åtminstone en rationell punkt ligger på den, och en rationell linje. Vi ser att ur diofantinanalysens synvinkel cirkeln C och rak Lär omöjliga att skilja: deras uppsättningar av rationella lösningar är likvärdiga. Och detta trots att ordningen på båda kurvorna är olika.

Mer subtil är klassificeringen av algebraiska kurvor efter släkte, som introducerades först på 1800-talet av Abel och Riemann. Denna klassificering tar hänsyn till antalet singulära punkter i kurvan Γ.

Vi antar att i ekvation (2) av kurvan Γ polynomet f (x , y) är irreducerbar över fältet för rationella tal, dvs. det expanderar inte till en produkt av polynom med rationella koefficienter. Som bekant är ekvationen för tangenten till kurvan Γ vid punkten P (x 0 , y 0) kommer

y – y 0 = k (x – x 0),

k = –

fx" (x 0 , y 0)

fy" (x 0 , y 0)

Om vid punkten P derivat fx" eller fy" skiljer sig från noll, sedan lutningen k tangent har en mycket bestämd betydelse (om fy" (x 0 , y 0) = 0, a fx" (x 0 , y 0) ≠ 0, alltså k=∞ och tangent vid P kommer att vara vertikal).

Om vid punkten P båda partiella derivator försvinner,

fx" (x 0 , y 0) = 0 och fy" (x 0 , y 0) = 0,

peka sedan P kallad särskild .

Till exempel vid kurvan y 2 = x 2 + x 3 poäng (0, 0) kommer att vara speciell, eftersom i den fx" = –2x – 3x 2 och fy" = 2y gå till noll.

Ris. 2.

De enklaste singularpunkterna är dubbla ettor, där minst en av derivatorna f xx "" , f xy "" Och f åå "" skiljer sig från noll. I fig. Figur 2 visar en dubbelpunkt där kurvan har två olika tangenter. Andra mer komplexa singulära punkter visas i fig. 3.

Ris. 3.

4. Lösningar

Regel 1. Om c inte är delbart med d, så har ekvationen ax + vy = c inga lösningar i heltal. N.O.D.(a,b) = d.

Regel 2. För att hitta en lösning på ekvationen ax + vy = c med coprime a och b måste du först hitta en lösning (X o; y o) till ekvationen ax + y = 1; talen CX o, Su o bildar en lösning till ekvationen ax + vy = c.

Lös ekvationen i heltal (x,y)

5x - 8y = 19 ... (1)

Första sättet. Att hitta en speciell lösning med hjälp av urvalsmetoden och spela in den allmänna lösningen.

Vi vet att om N.O.D.(a;b) =1, dvs. a och b är coprimtal, sedan ekvation (1)

har en lösning i heltal x och y. N.O.D.(5;8) =1. Med hjälp av urvalsmetoden hittar vi en speciell lösning: X o = 7; y o =2.

Så, talparet (7;2) är en speciell lösning till ekvation (1).

Det betyder att likheten gäller: 5 x 7 – 8 x 2 = 19 ... (2)

Fråga: Hur, givet en lösning, kan du skriva ner alla andra lösningar?

Låt oss subtrahera likhet (2) från ekvation (1) och få: 5(x -7) – 8(y - 2) =0.

Alltså x – 7 = . Av den resulterande likheten är det tydligt att talet (x – 7) blir ett heltal om och endast om (y – 2) är delbart med 5, d.v.s. y – 2 = 5n, där n är något heltal. Så, y = 2 + 5n, x = 7 + 8n, där n Z.

Således kan alla heltalslösningar av den ursprungliga ekvationen skrivas i följande form:

Andra sättet . Lösa en ekvation för en okänd.

Vi löser denna ekvation med avseende på det okända som har den minsta (modulo) koefficienten. 5x - 8y = 19 x = .

Återstoden dividerad med 5: 0,1,2,3,4. Låt oss ersätta y med dessa siffror.

Om y = 0, så är x = =.

Om y = 1 så är x = =.

Om y = 2, då är x = = = 7 Z.

Om y = 3 så är x = =.

Om y = 4 så är x = =.) Slutsats

Samtidigt har de flesta vetenskapshistoriker, i motsats till matematiker, hittills underskattat Diophantus verk. Många av dem trodde att Diophantus var begränsad till att bara hitta en lösning och använde konstgjorda tekniker för detta, olika för olika problem. Men faktiskt, i de flesta diofantiska ekvationer observerar vi liknande lösningsalgoritmer.

Idag finns det, som vi ser, flera olika lösningar, vars algoritmer är lätta att komma ihåg. Som nämnts tidigare finns denna ekvation vanligtvis i uppgift C6 på Unified State Exam. Att studera algoritmer för att lösa diofantiska ekvationer kan hjälpa till att lösa denna uppgift, som är värd ett betydande antal poäng.

Bibliografi

1. Diophantus av Alexandria. Aritmetik och en bok om polygonala tal (översättning från antik grekiska av I. N. Veselovsky; redigering och kommentarer av I. G. Bashmakova). M., "Science", 1974.

2. B. L. Van der Waerden, Awakening Science (översättning av I. N. Veselovsky). M., Fizmatgiz, 1959.

3. G. G. Tseyten, Matematikens historia under antiken och medeltiden (översättning av P. Jusjkevitj). M.–L., Gostekhizdat, 1932

4. A. V. Vasiliev, heltal. Petersburg, 1919

5. I. V. Yashchenko, S. A. Shestakov, P. I. Zakharov, Mathematics, Unified State Examination, MTsNMO, 2010

Diophantus av Alexandria(urgamla grekiska Διόφαντος ὁ Ἀλεξανδρεύς ; lat. Diophantus) är en antik grekisk matematiker som förmodligen levde på 300-talet e.Kr. e. Benämns ofta som "algebrans fader". Författare till "Aritmetik" - en bok tillägnad att hitta positiva rationella lösningar på obestämda ekvationer. Nuförtiden betyder "diofantiska ekvationer" vanligtvis ekvationer med heltalskoefficienter, vars lösningar måste hittas bland heltal.

Biografi [ | ]

Latinsk översättning Aritmetisk (1621)

Det motsvarar att lösa följande ekvation:

x = x 6 + x 12 + x 7 + 5 + x 2 + 4 (\displaystyle x=(\frac (x)(6))+(\frac (x)(12))+(\frac (x) (7))+5+(\frac (x)(2))+4)

Denna ekvation ger x = 84 (\displaystyle x=84), det vill säga åldern för Diophantus är lika med 84 år. Däremot kan riktigheten av informationen inte bekräftas.

Aritmetisk Diophanta[ | ]

Diophantus huvudverk - Aritmetisk i 13 böcker. Tyvärr har bara 6 (eller 10, se nedan) av de första 13 böckerna överlevt.

Inflytande Aritmetisk för matematikens utveckling[ | ]

På 900-talet Aritmetisköversattes till arabiska, varefter matematiker från islamiska länder (Abu Kamil och andra) fortsatte en del av Diophantus forskning. I Europa, intresse för Aritmetiskökade efter att Raphael Bombelli översatte och publicerade detta verk till latin och publicerade 143 problem från det i sin Algebra(1572). År 1621 kom en klassisk, grundligt kommenterad latinsk översättning Aritmetisk, avrättad av Bachet de Meziriac.

Andra verk av Diophantus[ | ]

Avhandling av Diophantus Om polygonala tal (Περὶ πολυγώνων ἀριθμῶν ) inte helt bevarad; i den bevarade delen härleds ett antal hjälpsatser med geometriska algebrametoder.

Från Diophantus verk Om att mäta ytor (ἐπιπεδομετρικά ) Och Om multiplikation (Περὶ πολλαπλασιασμοῦ ) har också bara fragment överlevt.

Diophantus bok Porismer känd endast från ett fåtal satser som används i Aritmetisk.

I avsnittet om frågan var bodde Diophantus ställd av författaren Lera... det bästa svaret är Diophantus - (sent 3:e århundradet e.Kr.) - berömd antik grekisk matematiker.
Det finns nästan ingen information om hans liv; inte ens datumen för hans födelse och död är helt tillförlitliga.
Bodde i den egyptiska staden Alexandria.
Diophantus verksamhet sammanföll med Greklands förfall, erövrat - som bekant - av Rom.
Grekiska vetenskapsmän fann en tillflyktsort i Egypten, främst i Alexandria, som vid den tiden hade blivit centrum för världskulturen.
Ett magnifikt bibliotek skapades i Alexandria, som vid Diophantus tid hade blivit centrum för världskulturen och humaniora, det så kallade biblioteket uppstod i Alexandria. Museion (musernas tempel eller helgedom), där aktiviteterna för de mest framstående representanterna för natur- och matematiska vetenskaper var koncentrerade.
Bland dessa forskare fanns Diophantus, en matematiker som tack vare sin bekantskap med syriska och indiska matematiker överförde babyloniernas prestationer inom algebraområdet till grekisk vetenskap.

Svar från Alexander[guru]
alla matematiker från Grekland

Svar från bidra[nybörjare]
Att döma av det faktum att han är Diophantus av Alexandria, bodde han i Alexandria (i det moderna Egyptens territorium) på 300-talet e.Kr. Förmodligen datumen för hans liv: född - 325, död - 409 e.Kr

Svar från Borra[nybörjare]
Diophantus av Alexandria?
Forntida romersk matematiker
En antik grekisk matematiker som förmodligen levde på 300-talet e.Kr. e. Benämns ofta som "algebrans fader". Författare till "Aritmetik" - en bok tillägnad att hitta positiva rationella lösningar på obestämda ekvationer. Nuförtiden betyder "diofantiska ekvationer" vanligtvis ekvationer med heltalskoefficienter, vars lösningar måste hittas bland heltal.

Bläckfiskar har 8 ben, sjöstjärnor har 5.

Hur många marina djur finns det i akvariet om det finns 39 lemmar totalt?

Diophantus av Alexandria är en antik grekisk matematiker som förmodligen levde på 300-talet e.Kr.

Nästan ingenting är känt om detaljerna i hans liv. Å ena sidan citerar Diophantus Hypsicles (2:a århundradet f.Kr.); å andra sidan skriver Theon av Alexandria (ca 350 e.Kr.) om Diophantus, varav vi kan dra slutsatsen att hans liv utspelade sig inom denna periods gränser. Ett möjligt förtydligande av tiden för Diophantus liv är baserat på det faktum att hans "Aritmetik" är tillägnad "den mest ärevördiga Dionysius". Man tror att denne Dionysius är ingen mindre än biskop Dionysius av Alexandria, som levde i mitten av 300-talet. n. e.

The Palatine Anthology innehåller en epigram-uppgift från vilken vi kan dra slutsatsen att Diophantus levde 84 år:

Diophantus aska vilar i graven; förundras över henne och stenen

Den avlidnes ålder kommer att tala genom hans kloka konst.

Enligt gudarnas vilja levde han en sjättedel av sitt liv som barn.

Och jag mötte halv sex med ludd på kinderna.

Strax efter den sjunde dagen förlovade han sig med sin flickvän.

Efter att ha tillbringat fem år med henne fick vismannen en son;

Hans fars älskade son levde bara halva sitt liv.

Han togs från sin far vid sin tidiga grav.

Två gånger två år sörjde föräldern en tung sorg,

Här såg jag gränsen för mitt sorgliga liv.

Med hjälp av moderna metoder för att lösa ekvationer är det möjligt att beräkna hur många år Diophantus levde. Låt oss skapa och lösa ekvationen:

Lösningen på denna ekvation är talet 84. Således levde Diophantus 84 år.

Diophantus huvudverk är "Aritmetik" i 13 böcker. Tyvärr har bara de första 6 böckerna av 13 överlevt.

Den första boken föregås av en omfattande introduktion, som beskriver den notation som Diophantus använder. Diophantus kallar det okända ett "tal" (?ριθμ?ς) och betecknar det med bokstaven ς, kvadraten på det okända med en symbol (förkortning för δ?ναμις - "grad"). Särskilda tecken tillhandahålls för följande grader av det okända, upp till den sjätte, kallad kubkuben, och för graderna motsatt dem. Diophantus har inget additionstecken: han skriver helt enkelt positiva termer bredvid varandra, och i varje term skrivs först graden av det okända och sedan den numeriska koefficienten. De subtraherade termerna skrivs också sida vid sida, och ett speciellt tecken i form av en inverterad bokstav Ψ placeras framför hela gruppen. Likhetstecknet betecknas med två bokstäver ?σ (förkortning för ?σος - "lika"). Regeln för att ta med liknande termer och regeln för att addera eller subtrahera samma tal eller uttryck på båda sidor av ekvationen formulerades: vad al-Khwarizmi senare kom att kalla "al-jabr och al-muqabala." En teckenregel har införts: minus gånger minus ger plus; Denna regel används när man multiplicerar två uttryck med subtraherade termer. Allt detta är formulerat i allmänna termer, utan hänvisning till geometriska tolkningar.

Det mesta av arbetet är en samling problem med lösningar (det finns totalt 189 i de sex bevarade böckerna), skickligt utvalda för att illustrera allmänna metoder. Huvudproblemet med "Aritmetik" är att hitta positiva rationella lösningar på obestämda ekvationer. Rationella tal tolkas av Diophantus på samma sätt som naturliga tal, vilket inte är typiskt för forntida matematiker.

Först undersöker Diophantus system av 2:a ordningens ekvationer i 2 okända; den specificerar en metod för att hitta andra lösningar om en redan är känd. Sedan tillämpar han liknande metoder på ekvationer av högre grader.

På 1000-talet översattes "Aritmetik" till arabiska, varefter matematiker från islamiska länder (Abu Kamil och andra) fortsatte en del av Diophantus forskning. I Europa ökade intresset för aritmetik efter att Raphael Bombelli upptäckt detta verk i Vatikanbiblioteket och publicerade 143 problem från det i sin Algebra (1572). År 1621 kom en klassisk, grundligt kommenterad latinsk översättning av "Aritmetik", utförd av Bachet de Meziriak. Diophantus metoder hade ett enormt inflytande på François Viète och Pierre Fermat; fungerade som utgångspunkten för studierna av Gauss och Euler. Men i modern tid brukar obestämda ekvationer lösas i heltal, och inte i rationella, som Diophantus gjorde.

Under 1900-talet, under namnet Diophantus, upptäcktes den arabiska texten i ytterligare fyra aritmetiska böcker. Vissa matematikhistoriker, efter att ha analyserat denna text, lade fram hypotesen att deras författare inte var Diophantus, utan en kommentator som var väl insatt i Diophantus metoder, troligen Hypatia.

Diophantus avhandling "Om polygonala siffror" (Περ? πολυγ?νων ?ριθμ?ν) har inte bevarats helt; i den bevarade delen härleds ett antal hjälpsatser med geometriska algebrametoder.

Från verken av Diophantus "Om mätning av ytor" (?πιπεδομετρικ?) och "Om multiplikation" (Περ? πολλαπλασιασμο?) har också bara fragment bevarats.

Diophantus bok "Porisms" är känd endast från ett fåtal satser som används inom aritmetiken.

Idag är ekvationen av formen

Var P- en heltalsfunktion (till exempel ett polynom med heltalskoefficienter), och variablerna tar heltalsvärden, kallade för att hedra den antika grekiska matematikern - Diophantine.

Förmodligen är den mest kända diofantiska ekvationen

Dess lösningar är pytagoreiska trillingar: (3; 4; 5), (6; 8; 10), (5; 12; 13), (12; 35; 37)...

Bevis på olösligheten i heltal av den diofantiska ekvationen

på (Fermat's Last Theorem) avslutades av den engelske matematikern Andrew Wiles 1994.

Ett annat exempel på en diofantisk ekvation är Pells ekvation

var är parametern när inte en exakt kvadrat.

Hilberts tionde problem är ett av 23 problem som David Hilbert föreslog den 8 augusti 1900 vid den andra internationella matematikkongressen. I Hilberts rapport är formuleringen av det tionde problemet den kortaste av alla:

Låt en diofantisk ekvation med godtyckliga okända och heltalsrationella numeriska koefficienter ges. Ange en metod med vilken det är möjligt, efter ett ändligt antal operationer, att avgöra om denna ekvation är lösbar i rationella heltal.

Att bevisa den algoritmiska olösligheten för detta problem tog cirka tjugo år och slutfördes av Yuri Matiyasevich 1970.

Till stor del tack vare Pappus av Alexandrias verksamhet (III-talet) har information om forntida vetenskapsmän och deras verk nått oss. Efter Apollonius (från 2:a århundradet f.Kr.) började en nedgång inom den antika vetenskapen. Inga nya djupa idéer dyker upp. År 146 f.Kr. e. Rom erövrar Grekland, och år 31 f.Kr. e. - Alexandria. Mot bakgrund av allmän stagnation och nedgång sticker den gigantiska gestalten av Diophantus av Alexandria, den siste av de stora forntida matematikerna, "algebrans fader", ut skarpt.

Följande matematiska objekt är uppkallade efter Diophantus: