heim › Salon › Grafische Methode zur Lösung eines Gleichungssystems. Lösen von Gleichungen, Ungleichungen und Systemen mithilfe von Funktionsgraphen

Grafische Methode zur Lösung eines Gleichungssystems. Lösen von Gleichungen, Ungleichungen und Systemen mithilfe von Funktionsgraphen

Präsentation und Lektion zum Thema: „Grafische Lösung quadratischer Gleichungen“

Zusätzliche Materialien
Liebe Benutzer, vergessen Sie nicht, Ihre Kommentare, Bewertungen und Wünsche zu hinterlassen! Alle Materialien wurden von einem Antivirenprogramm überprüft.

Lernhilfen und Simulatoren im Integral Online-Shop für die 8. Klasse
Potenzen und Wurzeln, Funktionen und Graphen

Graphen quadratischer Funktionen

In der letzten Lektion haben wir gelernt, wie man jede quadratische Funktion grafisch darstellt. Mit Hilfe solcher Funktionen können wir die sogenannten quadratischen Gleichungen lösen, die im Allgemeinen wie folgt geschrieben werden: $ax^2+bx+c=0$,
$a, b, c$ sind beliebige Zahlen, aber $a≠0$.
Leute, vergleicht die oben geschriebene Gleichung mit dieser: $y=ax^2+bx+c$.
Sie sind nahezu identisch. Der Unterschied besteht darin, dass wir statt $y$ $0$ geschrieben haben, d.h. $y=0$. Wie löst man dann quadratische Gleichungen? Das erste, was mir in den Sinn kommt, ist, einen Graphen der Parabel $ax^2+bx+c$ zu konstruieren und die Schnittpunkte dieses Graphen mit der Geraden $y=0$ zu finden. Es gibt andere Lösungen. Schauen wir sie uns anhand eines konkreten Beispiels an.

Methoden zur Lösung quadratischer Funktionen

Beispiel.
Lösen Sie die Gleichung: $x^2+2x-8=0$.

Lösung.
Methode 1. Lassen Sie uns die Funktion $y=x^2+2x-8$ grafisch darstellen und die Schnittpunkte mit der Geraden $y=0$ finden. Der Koeffizient höchsten Grades ist positiv, das heißt, die Äste der Parabel zeigen nach oben. Finden wir die Koordinaten des Scheitelpunkts:
$x_(c)=-\frac(b)(2a)=\frac(-2)(2)=-1$.
$y_(в)=(-1)^2+2*(-1)-8=1-2-8=-9$.

Nehmen wir den Punkt mit den Koordinaten $(-1;-9)$ als Ursprung des neuen Koordinatensystems und konstruieren darin einen Graphen der Parabel $y=x^2$.

Wir sehen zwei Schnittpunkte. Sie sind in der Grafik mit schwarzen Punkten markiert. Wir lösen die Gleichung nach x, also müssen wir die Abszissen dieser Punkte wählen. Sie betragen -4$ und 2$.
Somit besteht die Lösung der quadratischen Gleichung $x^2+2x-8=0$ aus zwei Wurzeln: $ x_1=-4$ und $x_2=2$.

Methode 2. Transformieren Sie die ursprüngliche Gleichung in die Form: $x^2=8-2x$.
Somit können wir diese Gleichung auf die übliche grafische Weise lösen, indem wir die Abszisse der Schnittpunkte der beiden Graphen $y=x^2$ und $y=8-2x$ ermitteln.
Wir haben zwei Schnittpunkte erhalten, deren Abszissen mit den in der ersten Methode erhaltenen Lösungen übereinstimmen, nämlich: $x_1=-4$ und $x_2=2$.

Methode 3.
Lassen Sie uns die ursprüngliche Gleichung in diese Form umwandeln: $x^2-8=-2x$.
Lassen Sie uns zwei Graphen $y=x^2-8$ und $y=-2x$ erstellen und ihre Schnittpunkte ermitteln.
Der Graph von $y=x^2-8$ ist eine um 8 Einheiten nach unten verschobene Parabel.
Wir haben zwei Schnittpunkte erhalten, und die Abszissen dieser Punkte sind dieselben wie in den beiden vorherigen Methoden, nämlich: $x_1=-4$ und $x_2=2$.

Methode 4.
Wählen wir das perfekte Quadrat in der ursprünglichen Gleichung aus: $x^2+2x-8=x^2+2x+1-9=(x+1)^2-9$.
Lassen Sie uns zwei Graphen der Funktionen $y=(x+1)^2$ und $y=9$ erstellen. Der Graph der ersten Funktion ist eine um eine Einheit nach links verschobene Parabel. Der Graph der zweiten Funktion ist eine gerade Linie parallel zur Abszissenachse, die durch die Ordinate verläuft und gleich $9$ ist.
Wieder einmal haben wir zwei Schnittpunkte der Graphen erhalten, und die Abszissen dieser Punkte stimmen mit denen überein, die in den vorherigen Methoden $x_1=-4$ und $x_2=2$ erhalten wurden.

Methode 5.
Teilen Sie die ursprüngliche Gleichung durch x: $\frac(x^2)(x)+\frac(2x)(x)-\frac(8)(x)=\frac(0)(x)$.
$x+2-\frac(8)(x)=0$.
$x+2=\frac(8)(x)$.
Lassen Sie uns diese Gleichung grafisch lösen und zwei Graphen $y=x+2$ und $y=\frac(8)(x)$ erstellen.
Wieder haben wir zwei Schnittpunkte, und die Abszissen dieser Punkte stimmen mit denen überein, die oben $x_1=-4$ und $x_2=2$ erhalten wurden.

Algorithmus zur grafischen Lösung quadratischer Funktionen

Leute, wir haben uns fünf Möglichkeiten angesehen, quadratische Gleichungen grafisch zu lösen. Bei jeder dieser Methoden stellte sich heraus, dass die Wurzeln der Gleichungen gleich waren, was bedeutet, dass die Lösung korrekt erhalten wurde.

Grundlegende Methoden zur grafischen Lösung quadratischer Gleichungen $ax^2+bx+c=0$, $a, b, c$ – beliebige Zahlen, aber $a≠0$:
1. Konstruieren Sie einen Graphen der Funktion $y=ax^2+bx+c$ und finden Sie die Schnittpunkte mit der Abszissenachse, die die Lösung der Gleichung darstellen.
2. Konstruieren Sie zwei Graphen $y=ax^2$ und $y=-bx-c$ und ermitteln Sie die Abszisse der Schnittpunkte dieser Graphen.
3. Konstruieren Sie zwei Graphen $y=ax^2+c$ und $y=-bx$ und ermitteln Sie die Abszisse der Schnittpunkte dieser Graphen. Der Graph der ersten Funktion ist eine Parabel, die je nach Vorzeichen der Zahl c entweder nach unten oder nach oben verschoben ist. Der zweite Graph ist eine gerade Linie, die durch den Ursprung verläuft.
4. Wählen Sie ein vollständiges Quadrat aus, das heißt, bringen Sie die ursprüngliche Gleichung in die Form: $a(x+l)^2+m=0$.
Konstruieren Sie zwei Graphen der Funktion $y=a(x+l)^2$ und $y=-m$ und finden Sie ihre Schnittpunkte. Der Graph der ersten Funktion ist eine Parabel, die je nach Vorzeichen der Zahl $l$ entweder nach links oder nach rechts verschoben ist. Der Graph der zweiten Funktion ist eine gerade Linie parallel zur Abszissenachse und schneidet die Ordinatenachse an einem Punkt gleich $-m$.
5. Teilen Sie die ursprüngliche Gleichung durch x: $ax+b+\frac(c)(x)=0$.
Konvertieren Sie in die Form: $\frac(c)(x)=-ax-b$.
Konstruieren Sie erneut zwei Graphen und finden Sie deren Schnittpunkte. Der erste Graph ist eine Hyperbel, der zweite Graph ist eine Gerade. Leider ist die grafische Methode zur Lösung quadratischer Gleichungen nicht immer eine gute Lösung. Die Schnittpunkte verschiedener Diagramme sind nicht immer ganze Zahlen oder können auf der Abszisse (Ordinate) sehr große Zahlen aufweisen, die nicht auf einem normalen Blatt Papier dargestellt werden können.

Lassen Sie uns alle diese Methoden anhand eines Beispiels deutlicher demonstrieren.

Beispiel.
Lösen Sie die Gleichung: $x^2+3x-12=0$,

Lösung.
Zeichnen wir die Parabel und ermitteln die Koordinaten der Eckpunkte: $x_(c)=-\frac(b)(2a)=\frac(-3)(2)=-1,5$.
$y_(в)=(-1,5)^2+2*(-1,5)-8=2,25-3-8=-8,75$.
Bei der Konstruktion einer solchen Parabel treten sofort Probleme auf, beispielsweise bei der korrekten Markierung des Scheitelpunkts der Parabel. Um die Ordinate des Scheitelpunkts genau zu markieren, müssen Sie eine Zelle mit 0,25 Skaleneinheiten auswählen. Bei diesem Maßstab müssen Sie um 35 Einheiten nach unten gehen, was unpraktisch ist. Wie auch immer, lasst uns unseren Zeitplan erstellen.
Das zweite Problem, auf das wir stoßen, besteht darin, dass der Graph unserer Funktion die x-Achse an einem Punkt schneidet, dessen Koordinaten nicht genau bestimmt werden können. Eine Näherungslösung ist möglich, aber Mathematik ist eine exakte Wissenschaft.
Daher ist die grafische Methode nicht die bequemste. Daher erfordert die Lösung quadratischer Gleichungen eine universellere Methode, die wir in den folgenden Lektionen untersuchen werden.

Probleme, die selbstständig gelöst werden müssen

1. Lösen Sie die Gleichung grafisch (auf alle fünf Arten): $x^2+4x-12=0$.
2. Lösen Sie die Gleichung mit einer beliebigen grafischen Methode: $-x^2+6x+16=0$.

Manchmal werden Gleichungen grafisch gelöst. Dazu müssen Sie die Gleichung so transformieren (sofern sie nicht bereits in transformierter Form dargestellt wird), dass links und rechts vom Gleichheitszeichen Ausdrücke stehen, für die Sie leicht Funktionsgraphen zeichnen können. Nehmen wir zum Beispiel die folgende Gleichung:
x² – 2x – 1 = 0

Wenn wir das algebraische Lösen quadratischer Gleichungen noch nicht untersucht haben, können wir versuchen, dies entweder durch Faktorisieren oder grafisch zu tun. Um eine solche Gleichung grafisch zu lösen, stellen wir sie in dieser Form dar:
x² = 2x + 1

Aus dieser Darstellung der Gleichung folgt, dass es notwendig ist, solche x-Werte zu finden, bei denen die linke Seite gleich der rechten ist.

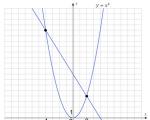
Wie Sie wissen, ist der Graph der Funktion y = x² eine Parabel und y = 2x + 1 eine Gerade. Die x-Koordinate der Punkte der Koordinatenebene, die sowohl auf dem ersten als auch auf dem zweiten Graphen liegen (also die Schnittpunkte der Graphen), sind genau die x-Werte, bei denen die linke Seite der Gleichung gleich ist Nach rechts. Mit anderen Worten: Die x-Koordinaten der Schnittpunkte der Graphen sind die Wurzeln der Gleichung.

Diagramme können sich an mehreren Punkten, an einem Punkt oder überhaupt nicht schneiden. Daraus folgt, dass eine Gleichung mehrere Wurzeln, eine Wurzel oder gar keine haben kann.

Schauen wir uns ein einfacheres Beispiel an:
x² – 2x = 0 oder x² = 2x

Zeichnen wir Graphen der Funktionen y = x² und y = 2x:

Wie aus der Zeichnung ersichtlich ist, schneiden sich die Parabel und die Gerade in den Punkten (0; 0) und (2; 4). Die x-Koordinaten dieser Punkte sind jeweils gleich 0 und 2. Das bedeutet, dass die Gleichung x² – 2x = 0 zwei Wurzeln hat – x 1 = 0, x 2 = 2.

Überprüfen wir dies, indem wir die Gleichung lösen, indem wir den gemeinsamen Faktor aus den Klammern entfernen:
x² – 2x = 0
x(x – 2) = 0

Die Null auf der rechten Seite kann entweder dann auftreten, wenn x 0 oder 2 ist.

Der Grund, warum wir die Gleichung x² – 2x – 1 = 0 nicht grafisch gelöst haben, liegt darin, dass in den meisten Gleichungen die Wurzeln reelle (Bruch-)Zahlen sind und es schwierig ist, den Wert von x in einem Diagramm genau zu bestimmen. Daher ist die grafische Lösung für die meisten Gleichungen nicht die beste. Die Kenntnis dieser Methode ermöglicht jedoch ein tieferes Verständnis der Beziehung zwischen Gleichungen und Funktionen.

>>Mathematik: Grafische Lösung von Gleichungen

Grafische Lösung von Gleichungen

Fassen wir unser Wissen darüber zusammen Grafiken Funktionen. Wir haben gelernt, wie man Diagramme der folgenden Funktionen erstellt:

y =b (gerade Linie parallel zur x-Achse);

y = kx (Linie durch den Ursprung);

y - kx + m (gerade Linie);

y = x 2 (Parabel).

Die Kenntnis dieser Diagramme ermöglicht es uns, bei Bedarf die analytische zu ersetzen Modell geometrisch (grafisch) betrachten Sie beispielsweise anstelle des Modells y = x 2 (das eine Gleichheit mit zwei Variablen x und y darstellt) eine Parabel in der Koordinatenebene. Insbesondere ist es manchmal nützlich, um Gleichungen zu lösen. Lassen Sie uns anhand einiger Beispiele besprechen, wie dies geschieht.

A. V. Pogorelov, Geometrie für die Klassen 7-11, Lehrbuch für Bildungseinrichtungen

Unterrichtsinhalte Unterrichtsnotizen unterstützender Rahmen Lektion Präsentation Beschleunigungsmethoden interaktive Technologien Üben Aufgaben und Übungen, Selbsttest, Workshops, Schulungen, Fälle, Quests, Hausaufgaben, Diskussionsfragen, rhetorische Fragen von Schülern Illustrationen Audio, Videoclips und Multimedia Fotografien, Bilder, Grafiken, Tabellen, Diagramme, Humor, Anekdoten, Witze, Comics, Gleichnisse, Sprüche, Kreuzworträtsel, Zitate Add-ons Zusammenfassungen Artikel, Tricks für Neugierige, Krippen, Lehrbücher, grundlegendes und zusätzliches Begriffswörterbuch, Sonstiges Verbesserung von Lehrbüchern und UnterrichtKorrektur von Fehlern im Lehrbuch Aktualisierung eines Fragments in einem Lehrbuch, Elemente der Innovation im Unterricht, Ersetzen veralteter Kenntnisse durch neues Nur für Lehrer perfekter Unterricht Kalenderplan für das Jahr; methodische Empfehlungen; Diskussionsprogramm Integrierter Unterricht

Es soll eine vollständige quadratische Gleichung vorliegen: A*x2+B*x+C=0, wobei A, B und C beliebige Zahlen sind und A ungleich Null ist. Dies ist ein allgemeiner Fall einer quadratischen Gleichung. Es gibt auch eine reduzierte Form mit A=1. Um eine Gleichung grafisch zu lösen, müssen Sie den Term mit dem höchsten Grad in einen anderen Teil verschieben und beide Teile einer Variablen gleichsetzen.

Danach bleibt A*x2 auf der linken Seite der Gleichung und B*x-C auf der rechten Seite (wir können davon ausgehen, dass B eine negative Zahl ist, das ändert nichts am Wesen). Die resultierende Gleichung lautet A*x2=B*x-C=y. Der Übersichtlichkeit halber werden in diesem Fall beide Teile mit der Variablen y gleichgesetzt.

Diagramme zeichnen und Ergebnisse verarbeiten

Jetzt können wir zwei Gleichungen schreiben: y=A*x2 und y=B*x-C. Als Nächstes müssen Sie für jede dieser Funktionen ein Diagramm zeichnen. Der Graph y=A*x2 ist eine Parabel mit einem Scheitelpunkt im Ursprung, deren Äste je nach Vorzeichen der Zahl A nach oben oder unten gerichtet sind. Ist sie negativ, sind die Äste nach unten gerichtet, ist sie positiv, die Zweige sind nach oben gerichtet.

Der Graph y=B*x-C ist eine regelmäßige Gerade. Wenn C=0, verläuft die Linie durch den Ursprung. Im allgemeinen Fall schneidet es von der Ordinatenachse ein Segment gleich C ab. Der Neigungswinkel dieser Linie relativ zur Abszissenachse wird durch den Koeffizienten B bestimmt. Er ist gleich dem Tangens der Neigung dieses Winkels.

Nachdem die Diagramme gezeichnet wurden, erkennt man, dass sie sich an zwei Punkten schneiden. Die Koordinaten dieser Punkte entlang der x-Achse bestimmen die Wurzeln der quadratischen Gleichung. Um sie genau zu bestimmen, müssen Sie Diagramme klar erstellen und den richtigen Maßstab auswählen.

Eine weitere grafische Lösung

Es gibt eine andere Möglichkeit, eine quadratische Gleichung grafisch zu lösen. Es ist nicht notwendig, B*x+C auf die andere Seite der Gleichung zu verschieben. Sie können die Funktion y=A*x2+B*x+C sofort zeichnen. Ein solcher Graph ist eine Parabel mit einem Scheitelpunkt an einem beliebigen Punkt. Diese Methode ist komplizierter als die vorherige, aber Sie können nur ein Diagramm erstellen, um ...

Zuerst müssen Sie den Scheitelpunkt der Parabel mit den Koordinaten x0 und y0 bestimmen. Seine Abszisse wird nach der Formel x0=-B/2*a berechnet. Um die Ordinate zu bestimmen, müssen Sie den resultierenden Abszissenwert in die ursprüngliche Funktion einsetzen. Mathematisch lässt sich diese Aussage wie folgt schreiben: y0=y(x0).

Dann müssen Sie zwei Punkte finden, die symmetrisch zur Achse der Parabel sind. In ihnen muss die ursprüngliche Funktion verschwinden. Danach können Sie eine Parabel bauen. Die Schnittpunkte mit der X-Achse ergeben zwei Wurzeln der quadratischen Gleichung.