hjem › Kropp › Diophantus-prosjektet og dets funn. Abstrakt: Diophantus

Diophantus-prosjektet og dets funn. Abstrakt: Diophantus

Koeffisienter hvis løsninger må finnes blant heltall.

Diophantus av Alexandria
Διόφαντος ὁ Ἀλεξανδρεύς

Fødselsdato	ikke tidligere og ikke senere eller
Fødselssted	Alexandria, Egypt
Dødsdato	ikke tidligere og ikke senere
Et land	Antikkens Roma
Vitenskapelig felt	tallteori
Kjent som	"far til algebra"
Diophantus av Alexandria på Wikimedia Commons

Biografi

Nesten ingenting er kjent om detaljene i livet hans. På den ene siden siterer Diophantus Hypsikler (2. århundre f.Kr.); på den annen side skriver Theon av Alexandria (ca. 350 e.Kr.) om Diophantus, hvorfra vi kan konkludere med at livet hans fant sted innenfor denne periodens grenser. En mulig avklaring av livstiden til Diophantus er basert på det faktum at han Aritmetikk dedikert til «den mest ærverdige Dionysius». Det antas at denne Dionysius er ingen ringere enn biskop Dionysius av Alexandria, som levde på midten av 300-tallet. n. e.

Det tilsvarer å løse følgende ligning:

x = x 6 + x 12 + x 7 + 5 + x 2 + 4 (\displaystyle x=(\frac (x)(6))+(\frac (x)(12))+(\frac (x) (7))+5+(\frac (x)(2))+4)

Denne ligningen gir x = 84 (\displaystyle x=84), det vil si at alderen til Diophantus er lik 84 år. Nøyaktigheten av informasjonen kan imidlertid ikke bekreftes.

Aritmetikk Diophanta

Hovedverket til Diophantus - Aritmetikk i 13 bøker. Dessverre har bare 6 (eller 10, se nedenfor) av de første 13 bøkene overlevd.

Den første boken er innledet med en omfattende introduksjon, som beskriver notasjonen som ble brukt av Diophantus. Diophantus kaller det ukjente "nummeret" ( ἀριθμός ) og er merket med bokstaven ς , firkant ukjent - symbol Δ Υ (kort for δύναμις - "grad"), kuben til det ukjente - symbol Κ Υ (kort for κύβος - "kube"). Spesielle tegn er gitt for følgende grader av det ukjente, opp til den sjette, kalt kube-kube, og for deres motsatte grader, opp til minus den sjette.

Diophantus har ikke et addisjonstegn: han skriver ganske enkelt positive termer ved siden av hverandre i synkende gradsrekkefølge, og i hvert ledd skrives først graden av det ukjente, og deretter den numeriske koeffisienten. De subtraherte leddene er også skrevet side om side, og et spesielt tegn i form av en invertert bokstav Ψ er plassert foran hele gruppen deres. Likhetstegnet er representert med to bokstaver ἴσ (kort for ἴσος - "lik").

En regel for å bringe lignende termer og en regel for å addere eller subtrahere samme tall eller uttrykk til begge sider av en ligning ble formulert: det al-Khorezmi senere begynte å kalle "algebra og almukabala." Tegnregelen er innført: «minus ved pluss gir minus», «minus ved minus gir pluss»; Denne regelen brukes når du multipliserer to uttrykk med subtraherte ledd. Alt dette er formulert i generelle termer, uten referanse til geometriske tolkninger.

Det meste av arbeidet er en samling av problemer med løsninger (det er totalt 189 i de seks bevarte bøkene, sammen med de fire fra den arabiske delen - 290), dyktig utvalgt for å illustrere generelle metoder. Hovedproblemer Aritmetikk- finne positive rasjonelle løsninger på usikre ligninger. Rasjonelle tall behandles av Diophantus på samme måte som naturlige tall, noe som ikke er typisk for gamle matematikere.

Først undersøker Diophantus systemer av andreordens ligninger i to ukjente; den spesifiserer en metode for å finne andre løsninger hvis en allerede er kjent. Så bruker han lignende metoder på ligninger av høyere grader. Bok VI undersøker problemer knyttet til rette trekanter med rasjonelle sider.

Innflytelse Aritmetikk for utvikling av matematikk

I det 10. århundre Aritmetikk ble oversatt til arabisk (se Kusta ibn Luka), hvoretter matematikere fra islamske land (Abu Kamil og andre) fortsatte noe av Diophantus sin forskning. I Europa, interesse for Aritmetikkøkte etter at Raphael Bombelli oversatte og publiserte dette verket til latin, og publiserte 143 problemer fra det i sin Algebra(1572). I 1621 dukket det opp en klassisk, grundig kommentert latinsk oversettelse Aritmetikk, henrettet av Bachet de Meziriac.

Diophantus' metoder påvirket i stor grad François Viète og Pierre Fermat; Men i moderne tid løses ubestemte ligninger vanligvis i heltall, og ikke i rasjonelle tall, slik Diophantus gjorde. Da Pierre Fermat leste Diophantus sin aritmetikk, redigert av Bachet de Mezyriac, kom han til den konklusjon at en av ligningene som ligner på de som ble vurdert av Diophantus ikke hadde noen løsninger i heltall, og bemerket i margen at han hadde funnet "et virkelig fantastisk bevis på denne teoremet ... men bokens marginer er for smale til å inkludere den." Denne uttalelsen er nå kjent som Fermats siste teorem.

På 1900-tallet ble den arabiske teksten til ytterligere fire bøker oppdaget under navnet Diophantus. Aritmetikk. I. G. Bashmakova og E. I. Slavutin, etter å ha analysert denne teksten, fremsatte en hypotese om at forfatteren ikke var Diophantus, men en kommentator som var godt kjent med Diophantus’ metoder, mest sannsynlig Hypatia. Imidlertid er det betydelige gapet i metodikken for å løse problemer i de tre første og tre siste bøkene godt fylt av fire bøker med arabisk oversettelse. Dette tvinger oss til å revurdere resultatene fra tidligere studier. . [ ]

Andre verk av Diophantus

Avhandling om Diophantus Om polygonale tall (Περὶ πολυγώνων ἀριθμῶν ) ikke fullstendig bevart; i den bevarte delen er en rekke hjelpesetninger utledet ved bruk av geometriske algebrametoder.

Fra verkene til Diophantus Om å måle overflater (ἐπιπεδομετρικά ) Og Om multiplikasjon (Περὶ πολλαπλασιασμοῦ ) også bare fragmenter har overlevd.

Diophantus bok Porismer bare kjent fra noen få teoremer brukt i Aritmetikk.

se også

Samling Budé" (2 bind utgitt: Bøkene 4 - 7).

Forskning:

Bashmakova I. G., Slavutin E. I., Rosenfeld B.A. Arabisk versjon av "Aritmetikk" av Diophantus // Historiske og matematiske studier. - M., 1978. - Utgave. XXIII. - S. 192 - 225.
Bashmakova I.G. Aritmetikk av algebraiske kurver: (Fra Diophantus til Poincaré) // Historiske og matematiske studier. - 1975. - Utgave. 20. - s. 104 - 124.
Bashmakova I.G. Diophantus og Diophantine ligninger. - M.: Nauka, 1972 (Reprint: M.: LKI, 2007). Per. På ham. Språk: Diophant und diophantische Gleichungen. - Basel; Stuttgart: Birkhauser, 1974. Trans. på engelsk. Språk: Diophantus og Diophantine ligninger/ Overs. av A. Shenitzer med redaksjonell bistand fra H. Grant og oppdatert av J. Silverman // The Dolciani Mathematical Expositions. - Nr. 20. - Washington, DC: Mathematical Association of America, 1997.
Bashmakova I.G. Diophantus og Fermat: (Om historien til metoden for tangenter og ekstrema) // Historiske og matematiske studier. - M., 1967. - Utgave. VII. - S. 185 - 204.
Bashmakova I. G., Slavutin E. I. Historien om Diophantine-analyse fra Diophantus til Fermat. - M.: Nauka, 1984.
Matematikkens historie fra antikken til begynnelsen av 1800-tallet. - T. I: Fra de eldste. ganger før begynnelsen av New Age. tid / red. A. P. Jusjkevitsj. - M., Nauka, 1970.
Slavutin E. I. Diophantus’ algebra og dens opprinnelse // Historiske og matematiske studier. - M., 1975. - Utgave. 20. - s. 63 - 103.
Shchetnikov A.I. Kan Diophantus av Alexandrias bok «Om polygonale tall» kalles rent algebraisk? // Historisk og matematisk forskning. - M., 2003. - Utgave. 8 (43). - s. 267 - 277.
Heath Th. L. Diophantus av Alexandria, en studie i historien til gresk algebra. - Cambridge, 1910 (Repr.: NY, 1964).
Knorr W.R. Arithmktikê stoicheiôsis: Om Diophantus og helten fra Alexandria // Historia Mathematica. - 20. - 1993. - S. 180 - 192.
Christianidis J. The way of Diophantus: Noen avklaringer på Diophantus’ løsningsmetode // Historia Mathematica. - 34. - 2007. - S. 289 - 305.
Rashed R., Houzel C. Les Arithmétiques de Diophante. Lecture historique et mathématique . - De Gruyter, 2013.

Kommunal utdanningsinstitusjon

"Lyceum nr. 10" Perm

Diophantus. Diofantiske ligninger

Gjort jobben

Ilyina Yana,

11. klasse elev

Veileder

Zolotukhina L. V.

matematikklærer

Perm, 2010

Introduksjon……………………………………………………………………………………………….3

1. Diophantus………………………………………………………………………………………..…4

2. Tall og symboler………………………………………………………………6

3. Diofantligning…………………………………………………..…8

4. Løsninger………………………………………………………………..12

Konklusjon………………………………………………………………………………………………………15

Referanser………………………………………………………………16

Introduksjon

Dagens skoleelever løser ulike ligninger. I del C av Unified State Examination-oppgavene er det en interessant ligning kalt Diophantine-ligningen. I sine arbeider stilte Diophantus ikke bare problemet med å løse ubestemte ligninger i rasjonelle tall, men ga også noen generelle metoder for å løse dem. Disse metodene vil være svært nyttige for dagens ellevteklassinger som skal ta matteeksamen.

Diophantus ga et like stort bidrag til utviklingen av matematikken som Arkimedes. Dette er hva Arkimedes gjorde, for eksempel: når han bestemte arealene til en ellipse, et segment av en parabel, overflaten av en kule, volumene til en kule og andre kropper, brukte han metoden for integral summer og metoden for passasje til det ytterste, men ingen steder ga han en generell abstrakt beskrivelse av disse metodene. Forskere på 1500- og 1600-tallet måtte nøye studere og omorganisere verkene hans på en ny måte for å isolere metodene til Arkimedes derfra. Situasjonen er lik med Diophantus. Metodene hans ble forstått og anvendt på nye problemer av Viethe og Fermat, dvs. på samme tid da Arkimedes ble løst.

1. Diophantus

Diophantus presenterer et av de vanskeligste mysteriene i vitenskapens historie. Vi kjenner ikke tiden da han levde, og heller ikke hans forgjengere som ville ha jobbet i samme felt. Hans verk er som en glitrende ild midt i fullstendig ugjennomtrengelig mørke. Tidsperioden da Diophantus kunne ha levd er et halvt årtusen! Den nedre grensen for dette intervallet bestemmes uten vanskeligheter: I sin bok om polygonale tall nevner Diophantus gjentatte ganger matematikeren Hypsicles of Alexandria, som levde i midten av det 2. århundre f.Kr. e. På den annen side, i kommentarene til Theon av Alexandria til "Almagest" til den berømte astronomen Ptolemaios, er et utdrag fra arbeidet til Diophantus plassert. Theon levde på midten av det 4. århundre e.Kr. e. Dette bestemmer den øvre grensen for dette intervallet. Altså 500 år!

Men bostedet til Diophantus er velkjent - dette er det berømte Alexandria, sentrum for vitenskapelig tanke i den hellenistiske verden.

For å uttømme alt som er kjent om personligheten til Diophantus, presenterer vi et gåtedikt som har kommet ned til oss:

Asken til Diophantus hviler i graven; forundre henne - og steinen
Den avdødes alder vil tale gjennom hans kloke kunst.
Etter gudenes vilje levde han en sjettedel av livet sitt som barn.
Og jeg møtte halv seks med lo på kinnene.
Det var bare den sjuende dagen han ble forlovet med kjæresten.
Etter å ha tilbrakt fem år med henne, ventet vismannen på sønnen sin;
Farens elskede sønn levde bare halve livet.
Han ble tatt fra sin far ved sin tidlige grav.
To ganger to år sørget forelderen over en tung sorg,
Her så jeg grensen for mitt triste liv.

Herfra er det lett å regne ut at Diophantus levde 84 år. Men for dette trenger du ikke å mestre kunsten til Diophantus! Det er nok å kunne løse en ligning av 1. grad med en ukjent, og egyptiske skriftlærde var i stand til å gjøre dette tilbake 2000 år f.Kr. e.

Men det mest mystiske er arbeidet til Diophantus. Seks bøker av 13 har nådd oss, som ble slått sammen til "Aritmetikk". Stilen og innholdet i disse bøkene skiller seg sterkt fra klassiske antikke verk om tallteori og algebra, eksempler på som vi kjenner fra Euklids elementer, hans data og lemmas fra verkene til Archimedes og Apollonius. "Aritmetikk" var utvilsomt resultatet av en rekke studier som forble helt ukjente for oss. Vi kan bare gjette om dens røtter og undre oss over rikdommen og skjønnheten til metodene og resultatene.

"Aritmetikk" av Diophantus er en samling av problemer (det er totalt 189), som hver er utstyrt med en løsning (eller flere løsningsmetoder) og nødvendige forklaringer. Derfor ser det ved første øyekast ut til at det ikke er et teoretisk arbeid. En nøye lesning viser imidlertid at problemene er nøye utvalgt og tjener til å illustrere svært spesifikke, strengt gjennomtenkte metoder. Som det var vanlig i oldtiden, er metoder ikke formulert i en generell form, men gjentas for å løse lignende problemer.

2. Tall og symboler

Diophantus begynner med grunnleggende definisjoner og en beskrivelse av bokstavsymbolene han skal bruke.

I klassisk gresk matematikk, som fant sin fullføring i Euklids elementer, under nummeret άριJμός - " arytmier"eller" aritmos"; derav navnet "aritmetikk" for vitenskapen om tall) ble forstått som et sett med enheter, dvs. heltall. Verken brøker eller irrasjonalitet ble kalt tall. Strengt tatt er det ingen brøker i Principia. Enheten anses som udelelig, og i stedet for brøkdeler av en enhet vurderes forholdstall av heltall; irrasjonaliteter opptrer som forholdstall av inkommensurable segmenter, for eksempel var tallet vi nå betegner √2 for de klassiske grekere forholdet mellom diagonalen til et kvadrat til siden. Det var ikke snakk om negative tall. Det var ikke engang noen ekvivalenter for dem. Vi finner et helt annet bilde hos Diophantus.

Diophantus gir den tradisjonelle definisjonen av tall som et sett med enheter, men søker senere etter sine problemer positiv rasjonell løsninger, og kaller hver slik løsning et tall (άριJμός - " arytmier »).

Men saken stopper ikke der. Diophantus introduserer negative tall: han kaller dem spesialbegrepet λει̃ψις - " leipsis" - avledet fra verbet λει̃πω - " leipo”, som betyr å mangle, å mangle, slik at selve begrepet kan oversettes med ordet “mangel”. Dette er forresten hva den berømte russiske vitenskapshistorikeren I. Timchenko gjør. Diophantus kaller et positivt tall ordet ΰπαρξις - " iparxis”, som betyr eksistens, væren, og i flertall kan dette ordet bety eiendom eller eiendom. Dermed er Diophantus sin terminologi for relative tall nær den som ble brukt i middelalderen i Østen og Europa. Mest sannsynlig var det ganske enkelt en oversettelse fra gresk til arabisk, sanskrit, latin og deretter til forskjellige språk i Europa.

Merk at begrepet λει̃ψις er " leipsis" - kan ikke oversettes som "subtrahert", slik mange oversettere av Diophantus gjør, fordi Diophantus bruker helt andre termer for subtraksjonen, nemlig άφελει̃ν - " afelein"eller άφαιρει̃ν -" avirrain", som er avledet fra verbet άφαιρεω - " afireo"- ta bort. Når han transformerer ligninger, bruker Diophantus selv ofte standarduttrykket "legg til λει̃ψις på begge sider."

Vi har dvelet så detaljert ved den filologiske analysen av Diophantus’ tekst for å overbevise leseren om at vi ikke vil avvike fra sannheten hvis vi oversetter Diophantus’ termer som «positive» og «negative».

Diophantus formulerer tegnregelen for relative tall:

"et negativt multiplisert med et negativt gir et positivt, mens et negativt multiplisert med et positivt gir et negativt, og kjennetegnet for en negativ er en invertert og forkortet (bokstav) ψ."

«Etter at jeg forklarte multiplikasjon for deg, blir også oppdelingen av de foreslåtte leddene tydelig; Nå vil det være greit å begynne å øve på addisjon, subtraksjon og multiplikasjon av slike ledd. Legg til positive og negative termer med forskjellige koeffisienter til andre termer som enten er positive eller like positive og negative, og fra positive og andre negative termer trekkes fra andre positive og like positive og negative termer."

Legg merke til at selv om Diophantus bare søker rasjonelle positive løsninger, bruker han villig negative tall i mellomberegninger.

Vi kan dermed merke oss at Diophantus utvidet tallfeltet til et felt med rasjonelle tall der alle fire aritmetiske operasjoner kan utføres uten hindring.

3. Diofantligning

Definisjon - algebraiske ligninger eller systemer av algebraiske ligninger med heltallskoeffisienter, som har et antall ukjente som overstiger antall ligninger, og som det søkes om heltallsløsninger eller rasjonelle løsninger for.

øks + av = 1

Hvor EN Og b- coprime heltall

Coprime tall flere heltall slik at felles divisorer for alle disse tallene bare er + 1 og - 1. Det minste multiplumet av et par primtall er lik deres produkt.

har uendelig mange løsninger:

Hvis x0 Og y0- én løsning, så tallene

X = x0 + bn

på = y0 -an

(n- ethvert heltall) vil også være løsninger.

Et annet eksempel på D. u.

x2 + y2 = z2

Positive heltallsløsninger til denne ligningen representerer lengdene på bena X , på og hypotenusen z rettvinklede trekanter med heltalls sidelengder kalles pytagoreiske tall.

trippel av naturlige tall slik at en trekant hvis sidelengder er proporsjonale (eller lik) med disse tallene er rektangulær.

Alle trillinger av coprime Pythagoras tall kan oppnås ved å bruke formlene

X = m2 - n2

på = 2mn

z = m2 + n2

Hvor m Og n- hele tall ( m > n > 0).

Denne ligningen definerer på planet R 2 algebraisk kurveΓ. Vi vil kalle den rasjonelle løsningen (2) rasjonelt poeng kurve Γ. I det følgende vil vi ofte ty til geometriens språk, selv om Diophantus selv ikke bruker det noe sted. Imidlertid har geometrisk språk nå blitt en så integrert del av matematisk tenkning at mange fakta vil være lettere å forstå og forklare ved hjelp av det.

Først av alt er det nødvendig å gi noen klassifisering av ligninger (2) eller, som er de samme, algebraiske kurver. Det mest naturlige og tidligste som oppstår er deres klassifisering etter rekkefølge.

La oss minne deg på det i rekkefølge kurve (2) er den maksimale rekkefølgen av leddene til polynomet f (x , y), der rekkefølgen til et ledd forstås som summen av potenser ved x Og y. Den geometriske betydningen av dette konseptet er at en rett linje skjærer en ordenskurve n nøyaktig kl n poeng. Når man teller poeng, må man selvfølgelig ta hensyn til mangfoldet av skjæringspunkter, så vel som komplekse og "uendelig fjerne" punkter. Så for eksempel en sirkel x 2 + y 2 = 1 og rett x + y= 2 skjærer i to komplekse punkter, og hyperbelen x 2 – y 2 = 1 og rett y =x- ved to punkter ved uendelig, den samme hyperbelen med en rett linje x=1 har ett felles multiplisitetspunkt 2.

Imidlertid for formålene diofantinanalyse(dette navnet ble gitt til feltet matematikk som vokste ut av problemene med å løse ubestemte ligninger; men nå kalles det oftere diofantinsk geometri) klassifisering etter rekkefølge viste seg å være for grov.

Ris. 1.

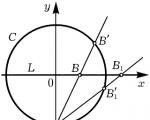
La oss forklare dette med et eksempel. La det gis en sirkel C : x 2 + y 2 = 1 og en hvilken som helst rett linje med rasjonelle koeffisienter, for eksempel, L : y=0. La oss vise at de rasjonelle punktene til denne sirkelen og linjen kan settes inn i en en-til-en korrespondanse. Dette kan for eksempel gjøres slik: fiks punktet EN(0,–1) sirkler og tilordner hvert rasjonelt punkt B rett L punkt B" sirkel C, liggende i krysset C og rett AB(Figur 1). At koordinatene til punktet B" vil være rasjonell, vil vi la leseren bevise det for seg selv eller lese et lignende bevis fra Diophantus (det vil bli presentert i neste avsnitt). Åpenbart kan den samme korrespondansen etableres mellom de rasjonelle punktene til ethvert kjeglesnitt, hvis minst ett rasjonelt punkt ligger på det, og en rasjonell linje. Vi ser at fra synspunktet til Diophantine analyse sirkelen C og rett L er umulig å skille: deres sett med rasjonelle løsninger er likeverdige. Og dette til tross for at rekkefølgen til begge kurvene er forskjellige.

Mer subtil er klassifiseringen av algebraiske kurver etter slekt, som ble introdusert først på 1800-tallet av Abel og Riemann. Denne klassifiseringen tar hensyn til antall enkeltpunkter på kurven Γ.

Vi antar at i ligning (2) av kurven Γ polynomet f (x , y) er irreduserbar over feltet for rasjonelle tall, dvs. den utvides ikke til et produkt av polynomer med rasjonelle koeffisienter. Som kjent er likningen av tangenten til kurven Γ ved punktet P (x 0 , y 0) vil

y – y 0 = k (x – x 0),

k = –

fx" (x 0 , y 0)

fy" (x 0 , y 0)

Hvis på punktet P derivat fx" eller fy" er forskjellig fra null, deretter helningen k tangent har en veldig bestemt betydning (hvis fy" (x 0 , y 0) = 0, a fx" (x 0 , y 0) ≠ 0, da k=∞ og tangent ved P vil være vertikal).

Hvis på punktet P begge partielle derivater forsvinner,

fx" (x 0 , y 0) = 0 og fy" (x 0 , y 0) = 0,

pek deretter P kalt spesiell .

For eksempel ved kurven y 2 = x 2 + x 3 poeng (0, 0) vil være spesielt, siden i det fx" = –2x – 3x 2 og fy" = 2y gå til null.

Ris. 2.

De enkleste entallspunktene er doble, hvor minst en av de deriverte f xx "" , f xy "" Og f åå "" er forskjellig fra null. I fig. Figur 2 viser et dobbeltpunkt hvor kurven har to forskjellige tangenter. Andre mer komplekse entallspunkter er vist i fig. 3.

Ris. 3.

4. Løsninger

Regel 1. Hvis c ikke er delelig med d, så har likningen ax + vy = c ingen løsninger i heltall. N.O.D.(a,b) = d.

Regel 2. For å finne en løsning på likningen ax + vy = c med coprime a og b, må du først finne en løsning (X o; y o) til likningen ax + y = 1; tallene CX o, Su o danner en løsning på ligningen ax + vy = c.

Løs ligningen i heltall (x,y)

5x - 8y = 19 ... (1)

Første vei. Finne en bestemt løsning ved å bruke valgmetoden og registrere den generelle løsningen.

Vi vet at hvis N.O.D.(a;b) =1, dvs. a og b er coprimtall, deretter ligning (1)

har en løsning i heltall x og y. N.O.D.(5;8) =1. Ved å bruke seleksjonsmetoden finner vi en spesiell løsning: X o = 7; y o =2.

Så tallparet (7;2) er en spesiell løsning på ligning (1).

Dette betyr at likheten gjelder: 5 x 7 – 8 x 2 = 19 ... (2)

Spørsmål: Hvordan, gitt én løsning, skrive ned alle de andre løsningene?

La oss trekke likhet (2) fra ligning (1) og få: 5(x -7) – 8(y - 2) =0.

Derfor x – 7 = . Fra den resulterende likheten er det klart at tallet (x – 7) vil være et heltall hvis og bare hvis (y – 2) er delelig med 5, dvs. y – 2 = 5n, hvor n er et heltall. Så, y = 2 + 5n, x = 7 + 8n, hvor n Z.

Dermed kan alle heltallsløsninger av den opprinnelige ligningen skrives i følgende form:

Andre vei . Løse en ligning for en ukjent.

Vi løser denne ligningen med hensyn til den ukjente som har den minste (modulo) koeffisienten. 5x - 8y = 19 x = .

Rester ved delt på 5: 0,1,2,3,4. La oss erstatte disse tallene med y.

Hvis y = 0, så er x = =.

Hvis y = 1, så er x = =.

Hvis y = 2, så er x = = = 7 Z.

Hvis y = 3, så er x = =.

Hvis y = 4, så er x = =.) Konklusjon

I mellomtiden har de fleste vitenskapshistorikere, i motsetning til matematikere, så langt undervurdert verkene til Diophantus. Mange av dem mente at Diophantus var begrenset til å finne bare én løsning og brukte kunstige teknikker for dette, forskjellige for ulike problemer. Men faktisk, i de fleste diofantiske ligninger observerer vi lignende løsningsalgoritmer.

I dag er det, som vi ser, flere forskjellige løsninger, algoritmene som er enkle å huske. Som nevnt tidligere, finnes denne ligningen vanligvis i oppgave C6 på Unified State Exam. Å studere algoritmer for å løse diofantiske ligninger kan hjelpe til med å løse denne oppgaven, som er verdt et betydelig antall poeng.

Bibliografi

1. Diophantus av Alexandria. Aritmetikk og en bok om polygonale tall (oversettelse fra gammelgresk av I. N. Veselovsky; redigering og kommentarer av I. G. Bashmakova). M., "Vitenskap", 1974.

2. B. L. Van der Waerden, Awakening Science (oversettelse av I. N. Veselovsky). M., Fizmatgiz, 1959.

3. G. G. Tseyten, Matematikkens historie i antikken og middelalderen (oversettelse av P. Yushkevich). M.–L., Gostekhizdat, 1932

4. A. V. Vasiliev, heltall. Petersburg, 1919

5. I. V. Yashchenko, S. A. Shestakov, P. I. Zakharov, Mathematics, Unified State Examination, MTsNMO, 2010

Diophantus av Alexandria(gamle grekerland Διόφαντος ὁ Ἀλεξανδρεύς ; lat. Diophantus) er en gammel gresk matematiker som antagelig levde på 300-tallet e.Kr. e. Ofte referert til som "algebraens far". Forfatter av "Aritmetikk" - en bok dedikert til å finne positive rasjonelle løsninger på ubestemte ligninger. I dag betyr "diofantiske ligninger" vanligvis ligninger med heltallskoeffisienter, hvis løsninger må finnes blant heltall.

Biografi [ | ]

Latinsk oversettelse Aritmetikk (1621)

Det tilsvarer å løse følgende ligning:

x = x 6 + x 12 + x 7 + 5 + x 2 + 4 (\displaystyle x=(\frac (x)(6))+(\frac (x)(12))+(\frac (x) (7))+5+(\frac (x)(2))+4)

Denne ligningen gir x = 84 (\displaystyle x=84), det vil si at alderen til Diophantus er lik 84 år. Nøyaktigheten av informasjonen kan imidlertid ikke bekreftes.

Aritmetikk Diophanta[ | ]

Hovedverket til Diophantus - Aritmetikk i 13 bøker. Dessverre har bare 6 (eller 10, se nedenfor) av de første 13 bøkene overlevd.

Innflytelse Aritmetikk for utvikling av matematikk[ | ]

I det 10. århundre Aritmetikk ble oversatt til arabisk, hvoretter matematikere fra islamske land (Abu Kamil og andre) fortsatte noe av Diophantus sin forskning. I Europa, interesse for Aritmetikkøkte etter at Raphael Bombelli oversatte og publiserte dette verket til latin, og publiserte 143 problemer fra det i sin Algebra(1572). I 1621 dukket det opp en klassisk, grundig kommentert latinsk oversettelse Aritmetikk, henrettet av Bachet de Meziriac.

Andre verk av Diophantus[ | ]

Fra verkene til Diophantus Om å måle overflater (ἐπιπεδομετρικά ) Og Om multiplikasjon (Περὶ πολλαπλασιασμοῦ ) også bare fragmenter har overlevd.

Diophantus bok Porismer bare kjent fra noen få teoremer brukt i Aritmetikk.

I avsnittet om spørsmålet hvor bodde Diophantus spurt av forfatteren Lera... det beste svaret er Diophantus - (sent 3. århundre e.Kr.) - kjent gammel gresk matematiker.
Det er nesten ingen informasjon om livet hans; selv datoene for hans fødsel og død er ikke helt pålitelige.
Bodde i den egyptiske byen Alexandria.
Aktiviteten til Diophantus falt sammen med nedgangen til Hellas, erobret - som kjent - av Roma.
Greske forskere fant tilflukt i Egypt, hovedsakelig i Alexandria, som på den tiden hadde blitt sentrum for verdenskulturen.
Et praktfullt bibliotek ble opprettet i Alexandria, som på Diophantus tid var blitt sentrum for verdenskultur og humaniora; det såkalte biblioteket oppsto i Alexandria. Museion (musenes tempel eller helligdom), hvor aktivitetene til de mest fremragende representantene for natur- og matematiske vitenskaper var konsentrert.
Blant disse forskerne var Diophantus, en matematiker som, takket være hans bekjentskap med syriske og indiske matematikere, overførte prestasjonene til babylonerne innen algebra til gresk vitenskap.

Svar fra Alexander[guru]
alle matematikere fra Hellas

Svar fra bidra[nybegynner]
Å dømme etter det faktum at han er Diophantus av Alexandria, bodde han i Alexandria (på territoriet til det moderne Egypt) på 300-tallet e.Kr. Antagelig datoene for hans liv: født - 325, død - 409 e.Kr

Svar fra Bore[nybegynner]
Diophantus av Alexandria?
Gammel romersk matematiker
En gammel gresk matematiker som visstnok levde i det 3. århundre e.Kr. e. Ofte referert til som "algebraens far". Forfatter av "Aritmetikk" - en bok dedikert til å finne positive rasjonelle løsninger på ubestemte ligninger. I dag betyr "diofantiske ligninger" vanligvis ligninger med heltallskoeffisienter, hvis løsninger må finnes blant heltall.

Blekkspruter har 8 bein, sjøstjerner har 5.

Hvor mange marine dyr er det i akvariet hvis det er 39 lemmer totalt?

Diophantus av Alexandria er en gammel gresk matematiker som antagelig levde i det 3. århundre e.Kr.

Nesten ingenting er kjent om detaljene i livet hans. På den ene siden siterer Diophantus Hypsikler (2. århundre f.Kr.); på den annen side skriver Theon av Alexandria (ca. 350 e.Kr.) om Diophantus, hvorfra vi kan konkludere med at livet hans fant sted innenfor denne periodens grenser. En mulig avklaring av tidspunktet for Diophantus' liv er basert på det faktum at hans "aritmetikk" er dedikert til "den mest ærverdige Dionysius." Det antas at denne Dionysius er ingen ringere enn biskop Dionysius av Alexandria, som levde på midten av 300-tallet. n. e.

The Palatine Anthology inneholder en epigram-oppgave som vi kan konkludere fra at Diophantus levde 84 år:

Asken til Diophantus hviler i graven; forundre henne og steinen

Den avdødes alder vil tale gjennom hans kloke kunst.

Etter gudenes vilje levde han en sjettedel av livet sitt som barn.

Og jeg møtte halv seks med lo på kinnene.

Like etter den syvende dagen forlovet han seg med kjæresten.

Etter å ha tilbrakt fem år med henne, fikk vismannen en sønn;

Farens elskede sønn levde bare halve livet.

Han ble tatt fra sin far ved sin tidlige grav.

To ganger to år sørget forelderen over en tung sorg,

Her så jeg grensen for mitt triste liv.

Ved hjelp av moderne metoder for å løse ligninger er det mulig å beregne hvor mange år Diophantus levde. La oss lage og løse ligningen:

Løsningen på denne ligningen er tallet 84. Dermed levde Diophantus 84 år.

Hovedverket til Diophantus er "Aritmetikk" i 13 bøker. Dessverre er det bare de første 6 bøkene av 13 som har overlevd.

Den første boken er innledet med en omfattende introduksjon, som beskriver notasjonen som ble brukt av Diophantus. Diophantus kaller det ukjente et "tall" (?ριθμ?ς) og betegner det med bokstaven ς, kvadratet på det ukjente med et symbol (forkortelse for δ?ναμις - "grad"). Spesielle tegn er gitt for følgende grader av det ukjente, opp til den sjette, kalt kuben-kuben, og for gradene motsatt av dem. Diophantus har ikke et addisjonstegn: han skriver ganske enkelt positive termer ved siden av hverandre, og i hvert ledd skrives først graden av det ukjente, og deretter den numeriske koeffisienten. De subtraherte leddene er også skrevet side om side, og et spesielt tegn i form av en invertert bokstav Ψ er plassert foran hele gruppen deres. Likhetstegnet er angitt med to bokstaver ?σ (forkortelse for ?σος - "lik"). Regelen for å bringe lignende termer og regelen for å legge til eller subtrahere det samme tallet eller uttrykket til begge sider av ligningen ble formulert: det al-Khwarizmi senere kom til å kalle "al-jabr og al-muqabala." Det er innført en tegnregel: minus ganger minus gir pluss; Denne regelen brukes når du multipliserer to uttrykk med subtraherte ledd. Alt dette er formulert i generelle termer, uten referanse til geometriske tolkninger.

Det meste av arbeidet er en samling problemer med løsninger (det er totalt 189 i de seks bevarte bøkene), dyktig utvalgt for å illustrere generelle metoder. Hovedproblemet med "aritmetikk" er å finne positive rasjonelle løsninger på ubestemte ligninger. Rasjonelle tall tolkes av Diophantus på samme måte som naturlige tall, noe som ikke er typisk for gamle matematikere.

Først undersøker Diophantus systemer av 2. ordens ligninger i 2 ukjente; den spesifiserer en metode for å finne andre løsninger hvis en allerede er kjent. Så bruker han lignende metoder på ligninger av høyere grader.

På 1000-tallet ble "aritmetikk" oversatt til arabisk, hvoretter matematikere fra islamske land (Abu Kamil og andre) fortsatte noe av Diophantus sin forskning. I Europa økte interessen for aritmetikk etter at Raphael Bombelli oppdaget dette verket i Vatikanets bibliotek og publiserte 143 problemer fra det i sin Algebra (1572). I 1621 dukket det opp en klassisk, grundig kommentert latinsk oversettelse av "Aritmetikk", utført av Bachet de Meziriak. Diophantus' metoder hadde en enorm innflytelse på François Viète og Pierre Fermat; fungerte som utgangspunkt for studiene til Gauss og Euler. Men i moderne tid løses ubestemte ligninger vanligvis i hele tall, og ikke i rasjonelle, slik Diophantus gjorde.

På 1900-tallet, under navnet Diophantus, ble den arabiske teksten til 4 flere aritmetiske bøker oppdaget. Noen matematikkhistorikere, etter å ha analysert denne teksten, fremsatte hypotesen om at forfatteren deres ikke var Diophantus, men en kommentator som var godt kjent med Diophantus’ metoder, mest sannsynlig Hypatia.

Diophantus sin avhandling «Om polygonale tall» (Περ? πολυγ?νων ?ριθμ?ν) er ikke fullstendig bevart; i den bevarte delen er en rekke hjelpesetninger utledet ved bruk av geometriske algebrametoder.

Fra verkene til Diophantus "Om måling av overflater" (?πιπεδομετρικ?) og "Om multiplikasjon" (Περ? πολλαπλασιασμο?) er også bare fragmenter bevart.

Diophantus bok "Porisms" er bare kjent fra noen få teoremer brukt i aritmetikk.

I dag er ligningen av formen

Hvor P- en heltallsfunksjon (for eksempel et polynom med heltallskoeffisienter), og variablene tar heltallsverdier, kalt til ære for den gamle greske matematikeren - Diophantine.

Sannsynligvis den mest kjente diofantiske ligningen er

Løsningene er pytagoreiske trillinger: (3; 4; 5), (6; 8; 10), (5; 12; 13), (12; 35; 37)...

Bevis på uløseligheten i heltall av den diofantiske ligningen

på (Fermat's Last Theorem) ble fullført av den engelske matematikeren Andrew Wiles i 1994.

Et annet eksempel på en diofantisk ligning er Pells ligning

hvor er parameteren n er ikke et eksakt kvadrat.

Hilberts tiende oppgave er en av 23 problemer som David Hilbert foreslo 8. august 1900 på den andre internasjonale matematikerkongressen. I Hilberts rapport er formuleringen av det tiende problemet den korteste av alle:

La en diofantligning med vilkårlige ukjente og heltallsrasjonelle numeriske koeffisienter gis. Angi en metode der det er mulig, etter et begrenset antall operasjoner, å bestemme om denne ligningen er løsbar i rasjonelle heltall.

Å bevise den algoritmiske uløseligheten til dette problemet tok omtrent tjue år og ble fullført av Yuri Matiyasevich i 1970.

Stort sett takket være aktivitetene til Pappus fra Alexandria (III århundre), har informasjon om gamle forskere og deres verk nådd oss. Etter Apollonius (fra det 2. århundre f.Kr.) begynte en tilbakegang i antikkens vitenskap. Ingen nye dype ideer dukker opp. I 146 f.Kr. e. Roma fanger Hellas, og i 31 f.Kr. e. - Alexandria. På bakgrunn av generell stagnasjon og tilbakegang, skiller den gigantiske figuren til Diophantus av Alexandria, den siste av de store gamle matematikerne, "algebraens far", seg skarpt ut.

Følgende matematiske objekter er oppkalt etter Diophantus: