집 › 몸 › Diophantus 프로젝트와 그 발견. 요약: 디오판토스

Diophantus 프로젝트와 그 발견. 요약: 디오판토스

정수 중에서 해를 찾아야 하는 계수입니다.

알렉산드리아의 디오판토스
Διόφαντος ὁ Ἀλεξανδρεύς

생일	더 이르지도 늦지도 않다또는
출생지	알렉산드리아, 이집트
사망일	더 이르지도 늦지도 않다
국가	고대 로마
과학 분야	정수론
로 알려진	"대수학의 아버지"
Wikimedia Commons의 알렉산드리아의 디오판토스

전기

그의 삶의 세부 사항에 대해서는 알려진 바가 거의 없습니다. 한편으로 Diophantus는 Hypsiles(기원전 2세기)를 인용합니다. 반면에 알렉산드리아의 테온(서기 350년경)은 디오판토스에 관해 글을 썼는데, 이로부터 우리는 그의 삶이 이 시대의 경계 내에서 일어났다는 결론을 내릴 수 있습니다. Diophantus의 생애에 대한 가능한 설명은 그가 다음과 같은 사실에 근거합니다. 산수"가장 존경받는 디오니시우스"에게 바쳐졌습니다. 이 디오니시우스는 다름 아닌 3세기 중반에 살았던 알렉산드리아의 디오니시우스 주교로 여겨진다. N. 이자형.

이는 다음 방정식을 푸는 것과 동일합니다.

x = x 6 + x 12 + x 7 + 5 + x 2 + 4 (\displaystyle x=(\frac (x)(6))+(\frac (x)(12))+(\frac (x) (7))+5+(\frac (x)(2))+4)

이 방정식은 x = 84 (\displaystyle x=84)즉, Diophantus의 나이는 84세입니다. 그러나 정보의 정확성은 확인할 수 없습니다.

산수디오판타

Diophantus의 주요 작품 - 산수 13권의 책으로. 불행하게도 처음 13권 중 6권(또는 10권, 아래 참조)만이 살아남았습니다.

첫 번째 책 앞에는 디오판토스가 사용한 표기법을 설명하는 광범위한 서문이 나옵니다. Diophantus는 알려지지 않은 "숫자"( ἀριθμός ) 문자로 표시됩니다. ς , 정사각형 알 수 없음 - 기호 Δ Υ (줄여서 δύναμις - "정도"), 미지의 입방체 - 기호 Κ Υ (줄여서 κύβος - "큐브"). 큐브-큐브라고 하는 6차까지의 미지의 차수와 그 반대 차수인 마이너스 6차까지에 대해 특수 기호가 제공됩니다.

Diophantus에는 덧셈 기호가 없습니다. 그는 단순히 내림차순으로 양의 용어를 나란히 쓰고 각 용어에 미지의 정도를 먼저 쓴 다음 수치 계수를 씁니다. 뺄셈 용어도 나란히 작성되며, 반전된 문자 Ψ 형태의 특수 기호가 전체 그룹 앞에 배치됩니다. 등호는 두 글자로 표현됩니다. ἴσ (줄여서 ἴσος - "동일한").

유사한 용어를 가져오는 규칙과 방정식의 양쪽에 동일한 숫자 또는 표현식을 더하거나 빼는 규칙이 공식화되었습니다. 이는 나중에 al-Khorezmi가 "대수학 및 알무카발라"라고 부르기 시작했습니다. 부호의 규칙이 도입되었습니다: “더하기로 마이너스를 하면 마이너스를 얻습니다”, “마이너스로 플러스를 하면 플러스를 얻습니다”; 이 규칙은 두 식에 뺄셈을 곱할 때 사용됩니다. 이 모든 것은 기하학적 해석을 참조하지 않고 일반적인 용어로 공식화됩니다.

대부분의 작업은 일반적인 방법을 설명하기 위해 능숙하게 선택된 솔루션 문제 모음입니다(6권의 책에는 총 189권, 아랍어 부분의 4권은 290권 포함). 주된 이슈 산수- 불확실한 방정식에 대한 긍정적이고 합리적인 해를 찾는 것입니다. 유리수는 Diophantus에 의해 자연수와 같은 방식으로 처리되는데, 이는 고대 수학자에게는 일반적이지 않습니다.

첫째, Diophantus는 두 가지 미지수로 2차 방정식 시스템을 조사합니다. 이미 알려진 다른 솔루션을 찾는 방법을 지정합니다. 그런 다음 그는 더 높은 차수의 방정식에 유사한 방법을 적용합니다. 제6권에서는 합리적인 변을 갖는 직각삼각형과 관련된 문제를 조사합니다.

영향 산수수학의 발전을 위해

10세기에 산수이 책은 아랍어로 번역되었으며(Kusta ibn Luka 참조), 그 후 이슬람 국가(Abu Kamil 및 기타)의 수학자들이 Diophantus의 연구 중 일부를 계속했습니다. 유럽에서는 관심이 산수 Raphael Bombelli가 이 작품을 라틴어로 번역하여 출판하고 그의 저서에 143개의 문제를 출판한 이후에 증가했습니다. 대수학(1572). 1621년에 철저하게 주석이 달린 고전적인 라틴어 번역본이 등장했습니다. 산수, Bachet de Meziriac이 처형했습니다.

Diophantus의 방법은 François Viète와 Pierre Fermat에 큰 영향을 미쳤습니다. 그러나 현대에는 부정 방정식은 일반적으로 Diophantus처럼 유리수가 아닌 정수로 풀립니다. 피에르 페르마(Pierre Fermat)는 Bachet de Mezyriac이 편집한 Diophantus의 산술(Arithmetic)을 읽었을 때 Diophantus가 고려한 것과 유사한 방정식 중 하나가 정수의 해를 갖지 않는다는 결론에 도달했으며 여백에 "진정으로 놀라운 증거"를 발견했다고 언급했습니다. 이 정리는 ... 하지만 책의 여백이 너무 좁아서 그것을 포함할 수 없습니다.” 이 진술은 이제 페르마의 마지막 정리로 알려져 있습니다.

20세기에는 디오판토스라는 이름으로 아랍어로 된 네 권의 책이 더 발견되었습니다. 산수. I. G. Bashmakova와 E. I. Slavutin은 이 텍스트를 분석한 후 저자가 Diophantus가 아니라 Diophantus의 방법에 정통한 주석가, 아마도 Hypatia일 것이라는 가설을 제시했습니다. 그러나 처음 3권과 마지막 3권의 문제 해결 방법론에 있어서 상당한 격차는 아랍어 번역본 4권이 잘 메워줍니다. 이로 인해 우리는 이전 연구 결과를 재고하게 됩니다. . [ ]

디오판토스의 다른 작품들

디오판토스의 논문 다각형 수에 대하여 (Περὶ πολυγώνων ἀριθμῶν ) 완전히 보존되지 않았습니다. 보존된 부분에서는 기하학적 대수학 방법을 사용하여 여러 가지 보조 정리가 파생됩니다.

디오판투스의 작품 중 측정면에 대하여 (ἐπιπεδομετρικά ) 그리고 곱셈에 대하여 (Περὶ πολλαπλασιασμοῦ ) 또한 단편만 살아 남았습니다.

디오판토스의 책 포리즘에 사용된 몇 가지 정리로만 알려져 있습니다. 산수.

또한보십시오

Collection Budé'(2권 출판: 4~7권).

연구:

Bashmakova I.G., Slavutin E.I., Rosenfeld B.A. Diophantus의 "산술"의 아랍어 버전 // 역사 및 수학 연구. - M., 1978. - 이슈. XXIII. -P.192-225.
바쉬마코바 I.G.대수 곡선의 산술: (Diophantus에서 Poincaré까지) // 역사 및 수학 연구. - 1975. - 이슈. 20. - 104 - 124 페이지.
바쉬마코바 I.G. Diophantus와 Diophantine 방정식. - M.: Nauka, 1972 (재인쇄: M.: LKI, 2007). 당. 그의 위에. 언어: 디오판트와 디오판티셰 글라이춘겐. - 바젤; 슈투트가르트: Birkhauser, 1974. Trans. 영어로. 언어: Diophantus 및 Diophantine 방정식/ 번역. H. Grant의 편집 지원을 받아 A. Shenitzer가 작성하고 J. Silverman이 업데이트함 // The Dolciani Mathematical Expositions. - 20번. - 워싱턴 DC: 미국 수학 협회, 1997.
바쉬마코바 I.G. Diophantus와 Fermat: (접선과 극단법의 역사에 대하여) // 역사적, 수학적 연구. - M., 1967. - 이슈. Ⅶ. -P.185-204.
Bashmakova I.G., Slavutin E.I.디오판투스(Diophantus)에서 페르마(Fermat)까지 디오판토스 분석의 역사. - M .: 나우카, 1984.
고대부터 19세기 초까지 수학의 역사를 다룬다. - T. I: 가장 오래된 것부터. 뉴 에이지가 시작되기 전의 시간. 시간 / 에드. A. P. Yushkevich. - M., 나우카, 1970.
슬라부틴 E. I. Diophantus의 대수학과 그 기원 // 역사 및 수학 연구. - M., 1975. - 이슈. 20. - 63 - 103 페이지.
셰트니코프 A.I.알렉산드리아의 디오판투스(Diophantus of Alexandria)의 책 "다각형 수에 대하여(On Polygonal Numbers)"를 순전히 대수학이라고 부를 수 있습니까? // 역사 및 수학적 연구. - M., 2003. - 이슈. 8 (43). - 267~277쪽.
히스 Th. 엘.알렉산드리아의 디오판토스, 그리스 대수학의 역사에 관한 연구. - 케임브리지, 1910(대표: NY, 1964).
크노르 W. R. Arithmktikê Stoicheiôsis: Diophantus와 Alexandria의 영웅에 관하여 // Historia Mathematica. - 20. - 1993. - P. 180 - 192.
크리스티안디스 J.디오판투스의 길: 디오판토스의 해결 방법에 대한 몇 가지 설명 // Historia Mathematica. - 34. - 2007. - P. 289 - 305.
래시드 R., 하우젤 C. Les Arithmétiques de Diophante. 역사와 수학 강의 . - 드 그뤼터, 2013.

시립 교육 기관

"Lyceum No. 10" 파마

디오판토스. 디오판토스 방정식

일을 마쳤다

일리나 야나,

11학년 학생

감독자

졸로투키나 L.V.

수학 선생님

페름, 2010

소개................................................................................................................3

1. 디오판토스..........................................................................................................4

2. 숫자 및 기호..........................................................................6

3. 디오판틴 방정식.............................................................................8

4. 솔루션..........................................................................................12

결론..........................................................................................................15

참고문헌..........................................................................16

소개

오늘날의 학생들은 다양한 방정식을 푼다. 통합 상태 시험 과제의 파트 C에는 디오판토스 방정식이라는 흥미로운 방정식이 있습니다. 그의 작품에서 디오판토스는 유리수로 부정 방정식을 푸는 문제를 제기했을 뿐만 아니라 이를 풀기 위한 몇 가지 일반적인 방법도 제시했습니다. 이러한 방법은 수학 시험을 앞두고 있는 11학년 학생들에게 매우 유용할 것입니다.

디오판토스는 아르키메데스만큼 수학 발전에 큰 공헌을 했습니다. 예를 들어 아르키메데스는 이렇게 했습니다. 타원의 면적, 포물선의 부분, 구의 표면, 구 및 기타 물체의 부피를 결정할 때 그는 적분 방법과 통과 방법을 사용했습니다. 한계까지 그는 이러한 방법에 대한 일반적인 추상 설명을 어디에도 제공하지 않았습니다. 16세기와 17세기의 과학자들은 아르키메데스의 방법을 거기에서 분리시키기 위해 그의 작품을 주의 깊게 연구하고 새로운 방식으로 재배열해야 했습니다. 상황은 Diophantus와 비슷합니다. 그의 방법은 Viethe와 Fermat에 의해 이해되고 새로운 문제에 적용되었습니다. 동시에 아르키메데스가 풀렸을 때.

1. 디오판토스

디오판토스는 과학 역사상 가장 어려운 미스터리 중 하나를 제시합니다. 그가 언제 살았는지, 같은 분야에서 일했던 그의 전임자들도 우리는 모릅니다. 그의 작품은 마치 꿰뚫을 수 없는 어둠 속에서 반짝이는 불과 같다. 디오판토스가 살 수 있었던 기간은 500년입니다! 이 간격의 하한은 쉽게 결정됩니다. 다각형 수에 관한 그의 책에서 Diophantus는 기원전 2세기 중반에 살았던 수학자 알렉산드리아의 Hypsicles를 반복적으로 언급합니다. 이자형. 한편, 유명한 천문학자 프톨레마이오스의 "알마게스트"에 대한 알렉산드리아의 테온의 논평에는 디오판투스의 연구에서 발췌한 내용이 실려 있습니다. 테온은 서기 4세기 중반에 살았습니다. 이자형. 이는 이 간격의 상한을 결정합니다. 그러니까 500년!

그러나 Diophantus의 거주지는 잘 알려져 있습니다. 이곳은 헬레니즘 세계의 과학적 사고의 중심지인 유명한 알렉산드리아입니다.

디오판투스의 성격에 대해 알려진 모든 것을 파악하기 위해 우리는 다음과 같은 수수께끼의 시를 제시합니다.

디오판토스의 재가 무덤에 안장되어 있습니다. 그녀와 돌에 놀라다
고인의 나이는 그의 현명한 예술을 통해 말할 것입니다.
신들의 뜻에 따라 그는 어린 시절의 6분의 1을 살았습니다.
그리고 5시 반에 뺨에 보풀이 생겼습니다.
그가 여자친구와 약혼한 것은 불과 일곱째 날이었습니다.
그녀와 함께 5년을 보낸 후 현자는 아들을 기다렸다.
그의 아버지가 사랑하는 아들은 인생의 절반밖에 살지 못했습니다.
그는 초기 무덤에서 아버지에게서 옮겨졌습니다.
2년 동안 두 번이나 그 부모는 큰 슬픔에 잠겼고,
여기서 나는 내 슬픈 삶의 한계를 보았다.

여기에서 디오판토스가 84년을 살았다는 것을 쉽게 계산할 수 있습니다. 그러나 이를 위해 Diophantus의 기술을 마스터할 필요는 없습니다! 미지의 방정식을 사용하여 1차 방정식을 풀 수 있으면 충분하며 이집트 서기관은 기원전 2천년 전에 이것을 할 수 있었습니다. 이자형.

그러나 가장 신비한 것은 Diophantus의 작품입니다. 13권 중 6권이 『산수』로 합쳐져서 우리에게 왔습니다. 이 책들의 스타일과 내용은 우리가 유클리드의 원소론, 데이터, 아르키메데스와 아폴로니우스의 작품에서 나온 기본정리 등을 통해 알 수 있는 정수론 및 대수학에 관한 고전 고대 작품과 크게 다릅니다. "산술"은 의심할 여지 없이 우리에게 전혀 알려지지 않은 수많은 연구의 결과였습니다. 우리는 그 뿌리를 추측할 수 있을 뿐이며 그 방법과 결과의 풍부함과 아름다움에 감탄할 뿐입니다.

Diophantus의 "산술"은 문제 모음(총 189개)으로, 각 문제에는 솔루션(또는 여러 솔루션 방법)과 필요한 설명이 포함되어 있습니다. 그러므로 얼핏 보면 이론적인 작업은 아닌 것처럼 보인다. 그러나 주의 깊게 읽어 보면 문제가 신중하게 선택되었으며 매우 구체적이고 엄격하게 고려된 방법을 설명하는 역할을 한다는 것을 알 수 있습니다. 고대의 관례처럼 방법은 일반적인 형태로 공식화되지 않고 유사한 문제를 해결하기 위해 반복됩니다.

2. 숫자 및 기호

Diophantus는 그가 사용할 문자 기호에 대한 기본 정의와 설명으로 시작합니다.

고전 그리스 수학에서는 유클리드의 원소에서 άριJμός라는 숫자로 완성되었습니다. 부정맥" 또는 " 산술"; 따라서 숫자 과학의 "산술"이라는 이름은 단위 집합으로 이해되었습니다. 정수. 분수도 무리수도 숫자라고 부르지 않았습니다. 엄밀히 말하면 프린키피아에는 분수가 없습니다. 단위는 나눌 수 없는 것으로 간주되며 단위의 분수 대신 정수의 비율이 고려됩니다. 비합리성은 측정할 수 없는 부분의 비율로 나타납니다. 예를 들어, 현재 우리가 표시하는 √2라는 숫자는 고대 그리스인에게 정사각형의 대각선과 그 변의 비율이었습니다. 음수에 대한 이야기는 없었습니다. 그들에게는 동등한 것이 없었습니다. 우리는 Diophantus에서 완전히 다른 그림을 발견합니다.

디오판투스는 수에 대한 전통적인 정의를 단위의 집합으로 제시하지만 나중에 그의 문제를 모색합니다. 긍정적 합리적솔루션을 지정하고 각 솔루션을 숫자(άριJμός - “ 부정맥 »).

그러나 문제는 여기서 끝나지 않습니다. Diophantus는 음수를 소개합니다. 그는 이를 특수 용어 λει̃ψις - "라고 부릅니다. 라이프시스" - 동사 λει̃πΩ에서 파생됨 - " 레이포”는 부족하다, 부족하다는 뜻이므로 용어 자체는 “부족하다”라는 단어로 번역될 수 있습니다. 그건 그렇고, 이것은 유명한 러시아 과학 역사가 I. Timchenko가하는 일입니다. Diophantus는 ΰπαρξις라는 단어를 양수라고 부릅니다. 아이파르시스”는 존재, 존재를 의미하며, 복수형으로 이 단어는 재산이나 재산을 의미할 수 있습니다. 따라서 상대수에 대한 디오판투스의 용어는 중세 동유럽과 유럽에서 사용된 용어와 유사합니다. 아마도 그것은 단순히 그리스어에서 아랍어, 산스크리트어, 라틴어로, 그리고 유럽의 다양한 언어로 번역되었을 것입니다.

λει̃ψις라는 용어는 " 라이프시스" - Diophantus의 많은 번역가처럼 "뺄셈"으로 번역할 수 없습니다. 왜냐하면 Diophantus는 뺄셈 작업에 완전히 다른 용어, 즉 άψελει̃ν - "를 사용하기 때문입니다. 아펠라인"또는 άφαιρει̃ν - " 불꽃놀이", 이는 동사 άταιρεΩ - "에서 파생됩니다. 아피레오"- 가져가세요. 방정식을 변환할 때 Diophantus 자신은 종종 "양변에 λει̃ψις를 추가합니다"라는 표준 표현을 사용합니다.

우리는 디오판투스의 용어를 "긍정적"과 "부정적"으로 번역하면 진리에서 벗어나지 않을 것이라는 점을 독자에게 확신시키기 위해 디오판토스 본문의 문헌학적 분석을 매우 자세히 설명했습니다.

Diophantus는 상대 수에 대한 부호의 규칙을 공식화합니다.

"음수에 음수를 곱하면 양수가 되고, 음수에 양수를 곱하면 음수가 되며, 음수를 구별하는 기호는 반전되고 단축된 (문자) ψ입니다."

“내가 당신에게 곱셈을 설명한 후에 제안된 용어의 구분도 분명해졌습니다. 이제 그러한 용어의 덧셈, 뺄셈, 곱셈 연습을 시작하는 것이 좋습니다. 계수가 다른 양수 및 음수 항을 양수 또는 동등 양수 및 음수인 다른 항에 추가하고 양수 및 기타 음수 항에서 다른 양수 및 동일 양수 및 음수 항을 뺍니다."

Diophantus는 합리적 양수 솔루션만을 추구하지만 중간 계산에서는 기꺼이 음수를 사용합니다.

따라서 우리는 디오판토스가 수의 장을 네 가지 산술 연산이 모두 방해 없이 수행될 수 있는 유리수의 장으로 확장했다는 점을 알 수 있습니다.

3. 디오판토스 방정식

정의 - 정수 계수를 갖는 대수 방정식 또는 대수 방정식 시스템으로, 방정식 수를 초과하는 미지수의 수가 많고 정수 또는 유리 해를 구하는 것입니다.

도끼 + ~에 의해 = 1

어디 ㅏ그리고 비- 서로소 정수

서로소수이 모든 숫자의 공약수는 + 1과 - 1뿐인 여러 정수. 소수 쌍의 가장 작은 배수는 그 곱과 같습니다.

무한히 많은 솔루션이 있습니다.

만약에 x0그리고 y0- 하나의 솔루션, 그 다음에는 숫자

엑스 = x0 + 억

~에 = y0 -안

(N- 임의의 정수)도 솔루션이 됩니다.

D.u의 또 다른 예입니다.

x2 + y2 = z2

이 방정식의 양의 정수 해는 다리의 길이를 나타냅니다. 엑스 , ~에그리고 빗변 지변의 길이가 정수인 직각삼각형을 피타고라스 수라고 합니다.

변의 길이가 이들 수에 비례하는(또는 동일한) 삼각형이 직사각형이 되도록 하는 자연수의 3배.

코프라임 피타고라스 수의 모든 삼중항은 다음 공식을 사용하여 얻을 수 있습니다.

엑스 = m2 - n2

~에 = 2백만

지 = m2 + n2

어디 중그리고 N- 정수( 중 > N > 0).

이 방정식은 평면에 정의됩니다. 아르 자형 2 대수학 곡선Γ. 우리는 합리적인 해결책을 부를 것입니다 (2) 합리적인 점곡선 Γ. 다음에서는 Diophantus 자신이 기하학 언어를 어디에도 사용하지 않지만 종종 기하학 언어에 의존하게 될 것입니다. 그러나 이제 기하학적 언어는 수학적 사고의 필수적인 부분이 되었기 때문에 많은 사실을 그 도움으로 이해하고 설명하기가 더 쉬워졌습니다.

우선, 방정식 (2) 또는 대수 곡선의 분류를 제공하는 것이 필요합니다. 가장 자연스럽고 가장 먼저 발생하는 것은 순서에 따른 분류입니다.

이를 상기시켜 드리겠습니다. 순서대로곡선 (2)는 다항식 항의 최대 차수입니다. 에프 (엑스 , 와이), 용어의 순서는 다음의 거듭제곱의 합으로 이해됩니다. 엑스그리고 와이. 이 개념의 기하학적 의미는 직선이 질서의 곡선과 교차한다는 것입니다. N정확히는 N포인트들. 물론 점을 계산할 때 교차점의 다양성과 복잡하고 "무한히 먼" 점을 고려해야 합니다. 예를 들어 원 엑스 2 + 와이 2 = 1 및 직선 엑스 + 와이= 2는 두 개의 복소점에서 교차하고 쌍곡선은 엑스 2 – 와이 2 = 1 및 직선 와이 =엑스- 무한대의 두 점에서 직선이 있는 동일한 쌍곡선 엑스=1은 다중성 2의 공통점이 하나 있습니다.

그러나 목적을 위해 디오판틴 분석(이 이름은 불확정 방정식을 푸는 문제에서 성장한 수학 분야에 주어졌지만 이제는 Diophantine 기하학이라고 더 자주 불립니다.) 순서에 따른 분류가 너무 거친 것으로 나타났습니다.

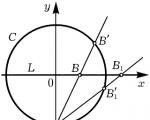
쌀. 1.

이를 예를 들어 설명하겠습니다. 원을 주자 씨 : 엑스 2 + 와이 2 = 1 및 유리수 계수를 갖는 임의의 직선, 예를 들어, 엘 : 와이=0. 이 원과 선의 유리점들이 일대일 대응이 될 수 있음을 보여드리겠습니다. 예를 들어 다음과 같이 할 수 있습니다. 점을 수정하세요. ㅏ(0,–1) 원을 그리며 각 유리점을 할당합니다. 비똑바로 엘가리키다 비"원 씨, 교차로에 누워 씨그리고 똑바로 AB(그림 1). 그 점의 좌표는 비"합리적이라면 독자가 스스로 증명하거나 Diophantus의 유사한 증명을 읽도록 할 것입니다(다음 단락에서 설명합니다). 분명히, 적어도 하나의 유리점이 그 위에 있는 경우 원뿔형 섹션의 유리점과 유리선 사이에 동일한 대응이 확립될 수 있습니다. 우리는 디오판토스 분석의 관점에서 원을 봅니다. 씨그리고 똑바로 엘구별할 수 없습니다. 합리적인 솔루션 세트는 동일합니다. 그리고 이는 두 곡선의 순서가 다르다는 사실에도 불구하고 발생합니다.

더 미묘한 것은 19세기에 Abel과 Riemann에 의해 소개된 속별 대수 곡선의 분류입니다. 이 분류에서는 곡선 Γ의 특이점 수를 고려합니다.

우리는 곡선 Γ의 방정식 (2)에서 다항식을 가정합니다. 에프 (엑스 , 와이)는 유리수 분야에서 환원 불가능합니다. 즉, 유리수 계수를 갖는 다항식의 곱으로 확장되지 않습니다. 알려진 바와 같이, 점에서 곡선 Γ에 대한 접선의 방정식 피 (엑스 0 , 와이 0) 그럴 것이다

와이 – 와이 0 = 케이 (엑스 – 엑스 0),

케이 = –

FX" (엑스 0 , 와이 0)

응" (엑스 0 , 와이 0)

만약 그 시점에 피유도체 FX"또는 응" 0과 다른 경우 기울기는 케이접선은 매우 명확한 의미를 갖습니다(만약 응" (엑스 0 , 와이 0) = 0, FX" (엑스 0 , 와이 0) ≠ 0이면 케이= 과 접선 피수직이 됩니다.)

만약 그 시점에 피두 부분 파생 상품이 모두 사라지고,

FX" (엑스 0 , 와이 0) = 0 및 응" (엑스 0 , 와이 0) = 0,

그럼 가리켜 피~라고 불리는 특별한 .

예를 들어 곡선에서 와이 2 = 엑스 2 + 엑스 3점(0, 0)은 특별할 것입니다. FX" = –2엑스 – 3엑스 2 및 응" = 2와이 0으로 가십시오.

쌀. 2.

가장 단순한 특이점은 이중 점이며, 여기서 도함수 중 적어도 하나는 에프xx "" , fxy ""그리고 에휴 ""제로와는 다릅니다. 그림에서. 그림 2는 곡선에 두 개의 서로 다른 접선이 있는 이중 점을 보여줍니다. 다른 더 복잡한 특이점은 그림 1에 나와 있습니다. 삼.

쌀. 삼.

4. 솔루션

규칙 1. c가 d로 나누어지지 않으면 방정식 ax + vy = c에는 정수의 해가 없습니다. N.O.D.(a,b) = d.

규칙 2. 서로소 a와 b가 있는 방정식 ax + vy = c의 해를 찾으려면 먼저 방정식 ax + y = 1의 해(X o; y o)를 찾아야 합니다. 숫자 CX o, Su o는 방정식 ax + vy = c에 대한 해를 형성합니다.

방정식을 정수(x,y)로 풀어보세요.

5x - 8y = 19 ... (1)

첫 번째 방법. 선택방법을 이용하여 특정해를 찾고, 일반적인 해를 기록한다.

N.O.D.(a;b) =1이면, 즉 a와 b는 서로 소수이고, 방정식 (1)

정수 x와 y의 해를 가집니다. N.O.D.(5;8) =1. 선택 방법을 사용하여 특정 솔루션을 찾습니다. X o = 7; 요 =2.

따라서 숫자 쌍 (7;2)은 방정식 (1)에 대한 특정 솔루션입니다.

이는 평등이 성립함을 의미합니다: 5 x 7 – 8 x 2 = 19 ... (2)

질문: 하나의 해결책이 주어졌을 때 다른 해결책을 모두 적는 방법은 무엇입니까?

방정식 (1)에서 평등 (2)를 빼고 다음을 얻습니다: 5(x -7) – 8(y - 2) =0.

따라서 x – 7 = . 결과적인 동등성으로부터 (y – 2)가 5로 나누어지는 경우에만 숫자 (x – 7)가 정수가 될 것이라는 것이 분명해졌습니다. 즉, y – 2 = 5n, 여기서 n은 정수입니다. 따라서 y = 2 + 5n, x = 7 + 8n, 여기서 n은 Z입니다.

따라서 원래 방정식의 모든 정수 해는 다음 형식으로 작성될 수 있습니다.

두 번째 방법 . 미지의 방정식을 푼다.

우리는 가장 작은 (모듈로) 계수를 갖는 미지수에 대해 이 방정식을 푼다. 5x - 8년 = 19 x = .

5로 나눈 나머지: 0,1,2,3,4. 이 숫자를 y로 대체해 보겠습니다.

y = 0이면 x = =입니다.

y = 1이면 x = =입니다.

y = 2이면 x = = = 7 Z입니다.

y = 3이면 x = =입니다.

y = 4이면 x = =입니다.) 결론

한편, 수학자들이 아닌 대부분의 과학사가들은 지금까지 디오판투스의 작품을 과소평가해 왔습니다. 그들 중 많은 사람들은 Diophantus가 단 하나의 해결책을 찾는 것으로 제한되어 있으며 이를 위해 다양한 문제에 대해 다른 인공 기술을 사용했다고 믿었습니다. 그러나 사실 대부분의 디오판토스 방정식에서 우리는 유사한 해법 알고리즘을 관찰합니다.

오늘날 우리가 볼 수 있듯이 알고리즘을 기억하기 쉬운 여러 가지 솔루션이 있습니다. 앞서 언급했듯이 이 방정식은 일반적으로 통합 상태 시험의 작업 C6에서 찾을 수 있습니다. 디오판토스 방정식을 풀기 위한 알고리즘을 연구하면 상당한 점수를 얻을 수 있는 이 작업을 해결하는 데 도움이 될 수 있습니다.

서지

1. 알렉산드리아의 디오판토스. 산술 및 다각형 숫자에 관한 책(I. N. Veselovsky의 고대 그리스어 번역, I. G. Bashmakova의 편집 및 의견). M., “과학”, 1974.

2. B. L. Van der Waerden, Awakening Science (I. N. Veselovsky 번역). 엠., 피즈마트기즈, 1959.

3. G. G. Tseyten, 고대와 중세 수학의 역사(P. Yushkevich 번역). M.–L., 고스테키즈다트, 1932

4. A. V. Vasiliev, 정수. 1919년 상트페테르부르크

5. I. V. Yashchenko, S. A. Shestakov, P. I. Zakharov, 수학, 통합 국가 시험, MTsNMO, 2010

알렉산드리아의 디오판토스(고대 그리스 Διόφαντος ὁ Ἀλεξανδρεύς ; 위도 디오판토스(Diophantus)는 아마도 AD 3세기에 살았던 고대 그리스 수학자이다. 이자형. 흔히 '대수학의 아버지'라고 불린다. "산술(Arithmetic)"의 저자 - 불확정 방정식에 대한 긍정적이고 합리적인 해를 찾는 데 전념하는 책입니다. 요즘 "디오판토스 방정식"은 일반적으로 정수 계수를 갖는 방정식을 의미하며, 그 해는 정수 중에서 찾아야 합니다.

전기 [ | ]

라틴어 번역 산수 (1621)

이는 다음 방정식을 푸는 것과 동일합니다.

x = x 6 + x 12 + x 7 + 5 + x 2 + 4 (\displaystyle x=(\frac (x)(6))+(\frac (x)(12))+(\frac (x) (7))+5+(\frac (x)(2))+4)

이 방정식은 x = 84 (\displaystyle x=84)즉, Diophantus의 나이는 84세입니다. 그러나 정보의 정확성은 확인할 수 없습니다.

산수디오판타[ | ]

Diophantus의 주요 작품 - 산수 13권의 책으로. 불행하게도 처음 13권 중 6권(또는 10권, 아래 참조)만이 살아남았습니다.

영향 산수수학의 발전을 위해[ | ]

10세기에 산수이 책은 아랍어로 번역되었으며, 그 후 이슬람 국가(아부 카밀 등)의 수학자들이 디오판투스의 연구 일부를 계속했습니다. 유럽에서는 관심이 산수 Raphael Bombelli가 이 작품을 라틴어로 번역하여 출판하고 그의 저서에 143개의 문제를 출판한 이후에 증가했습니다. 대수학(1572). 1621년에 철저하게 주석이 달린 고전적인 라틴어 번역본이 등장했습니다. 산수, Bachet de Meziriac이 처형했습니다.

디오판토스의 다른 작품들[ | ]

디오판토스의 책 포리즘에 사용된 몇 가지 정리로만 알려져 있습니다. 산수.

저자가 Diophantus가 어디에 살았는지에 대한 질문 섹션에서 레라...가장 좋은 대답은 Diophantus - (서기 3세기 말) - 유명한 고대 그리스 수학자.
그의 삶에 대한 정보는 거의 없습니다. 그의 생년월일과 사망일조차도 완전히 신뢰할 수 없습니다.
이집트 도시 알렉산드리아에 살았습니다.
Diophantus의 활동은 알려진 바와 같이 로마에 의해 정복된 그리스의 쇠퇴와 일치했습니다.
그리스 과학자들은 당시 세계 문화의 중심지가 된 이집트, 주로 알렉산드리아에서 피난처를 찾았습니다.
Diophantus 시대에 세계 문화와 인문학의 중심지가 된 알렉산드리아에 웅장한 도서관이 만들어졌고 소위 도서관이 알렉산드리아에 생겼습니다. 자연 과학과 수학 과학의 가장 뛰어난 대표자들의 활동이 집중된 Museion (뮤즈의 사원 또는 성소).
이 과학자 중에는 시리아와 인도 수학자와의 친분 덕분에 대수학 분야에서 바빌로니아인의 업적을 그리스 과학으로 옮긴 수학자 디오판투스(Diophantus)가 있었습니다.

답변 알렉산더[전문가]
그리스 출신의 모든 수학자

답변 기여하다[초보]
그가 알렉산드리아의 디오판토스라는 사실로 판단하면, 그는 서기 3세기에 알렉산드리아(현대 이집트 영토)에 살았습니다. 아마도 그의 생애 날짜는 다음과 같습니다. 출생 – 325년, 사망 – 서기 409년

답변 송곳[초보]
알렉산드리아의 디오판토스?
고대 로마 수학자
서기 3세기에 살았던 것으로 추정되는 고대 그리스 수학자. 이자형. 흔히 '대수학의 아버지'라고 불린다. "산술(Arithmetic)"의 저자 - 불확정 방정식에 대한 긍정적이고 합리적인 해를 찾는 데 전념하는 책입니다. 요즘 "디오판토스 방정식"은 일반적으로 정수 계수를 갖는 방정식을 의미하며, 그 해는 정수 중에서 찾아야 합니다.

문어의 다리는 8개, 불가사리의 다리는 5개입니다.

팔다리가 총 39개라면 수족관에 해양 동물은 몇 마리나 있나요?

알렉산드리아의 디오판토스(Diophantus of Alexandria)는 아마도 서기 3세기에 살았던 것으로 추정되는 고대 그리스 수학자이다.

그의 삶의 세부 사항에 대해서는 알려진 바가 거의 없습니다. 한편으로 Diophantus는 Hypsiles(기원전 2세기)를 인용합니다. 반면에 알렉산드리아의 테온(서기 350년경)은 디오판토스에 관해 글을 썼는데, 이로부터 우리는 그의 삶이 이 시대의 경계 내에서 일어났다는 결론을 내릴 수 있습니다. 디오판토스의 생애 시기를 명확하게 설명할 수 있는 방법은 그의 "산술"이 "가장 존경받는 디오니시우스"에게 헌정되었다는 사실에 근거합니다. 이 디오니시우스는 다름 아닌 3세기 중반에 살았던 알렉산드리아의 디오니시우스 주교로 여겨진다. N. 이자형.

Palatine Anthology에는 Diophantus가 84년을 살았다는 결론을 내릴 수 있는 경구 작업이 포함되어 있습니다.

디오판토스의 재가 무덤에 안장되어 있습니다. 그녀와 돌에 놀라다

고인의 나이는 그의 현명한 예술을 통해 말할 것입니다.

신들의 뜻에 따라 그는 어린 시절의 6분의 1을 살았습니다.

그리고 5시 반에 뺨에 보풀이 생겼습니다.

일곱째 날이 지나서 그는 여자친구와 약혼했습니다.

그녀와 5년을 보낸 후 현자는 아들을 낳았습니다.

그의 아버지가 사랑하는 아들은 인생의 절반밖에 살지 못했습니다.

그는 초기 무덤에서 아버지에게서 옮겨졌습니다.

2년 동안 두 번이나 그 부모는 큰 슬픔에 잠겼고,

여기서 나는 내 슬픈 삶의 한계를 보았다.

방정식을 푸는 현대적인 방법을 사용하면 Diophantus가 몇 년 동안 살았는지 계산할 수 있습니다. 방정식을 만들고 풀어 봅시다:

이 방정식의 해는 숫자 84입니다. 따라서 디오판토스는 84년을 살았습니다.

디오판토스의 주요 저작은 13권의 『산술』이다. 불행하게도 13권 중 처음 6권만 살아남았습니다.

첫 번째 책 앞에는 디오판토스가 사용한 표기법을 설명하는 광범위한 서문이 나옵니다. Diophantus는 미지의 것을 "숫자"(?ριθμ?ς)라고 부르고 기호(δ?ναμις - "degree"의 약자)가 있는 미지의 제곱인 문자 ς로 표시합니다. 큐브-큐브라고 불리는 미지의 다음 차수(최대 6차)와 그 반대 차수에 대해 특수 기호가 제공됩니다. Diophantus에는 추가 기호가 없습니다. 그는 단순히 양수 용어를 서로 옆에 쓰고 각 용어에 미지의 정도를 먼저 쓴 다음 수치 계수를 씁니다. 뺄셈 용어도 나란히 작성되며, 반전된 문자 Ψ 형태의 특수 기호가 전체 그룹 앞에 배치됩니다. 등호는 두 글자 ?σ(?σος의 약자 - "동등")로 표시됩니다. 유사한 용어를 가져오는 규칙과 방정식의 양쪽에 동일한 숫자 또는 표현식을 더하거나 빼는 규칙이 공식화되었습니다. 알-콰리즈미는 나중에 "알-자브르 및 알-무카발라"라고 부르게 되었습니다. 부호 규칙이 도입되었습니다. 마이너스 곱하기 마이너스는 플러스를 제공합니다. 이 규칙은 두 식에 뺄셈을 곱할 때 사용됩니다. 이 모든 것은 기하학적 해석을 참조하지 않고 일반적인 용어로 공식화됩니다.

대부분의 작업은 일반적인 방법을 설명하기 위해 능숙하게 선택된 솔루션 문제 모음(현재 남아 있는 6권의 책에 총 189개)입니다. "산술"의 주요 문제는 불확정 방정식에 대한 긍정적이고 합리적인 해를 찾는 것입니다. 유리수는 Diophantus에 의해 자연수와 같은 방식으로 해석되는데, 이는 고대 수학자에게는 일반적이지 않습니다.

첫째, Diophantus는 2개의 미지수로 2차 방정식 시스템을 조사합니다. 이미 알려진 다른 솔루션을 찾는 방법을 지정합니다. 그런 다음 그는 더 높은 차수의 방정식에 유사한 방법을 적용합니다.

10세기에 "산술"이 아랍어로 번역되었으며, 그 이후 이슬람 국가(아부 카밀 등)의 수학자들이 디오판투스의 연구 중 일부를 계속했습니다. 유럽에서는 라파엘 봄벨리(Raphael Bombelli)가 바티칸 도서관에서 이 작품을 발견하고 그의 대수학(Algebra, 1572)에서 143개의 문제를 출판한 이후 산술에 대한 관심이 높아졌습니다. 1621년에 바셰 드 메지리아크(Bachet de Meziriak)가 수행한 "산술(Arithmetic)"의 고전적이고 철저하게 논평된 라틴어 번역이 등장했습니다. Diophantus의 방법은 François Viète와 Pierre Fermat에게 큰 영향을 미쳤습니다. 가우스와 오일러 연구의 출발점이 되었습니다. 그러나 현대에는 부정 방정식이 일반적으로 Diophantus처럼 유리수 방정식이 아닌 정수로 풀립니다.

20세기에는 디오판투스(Diophantus)라는 이름으로 산수학 책 4권의 아랍어 텍스트가 더 발견되었습니다. 일부 수학 역사가들은 이 텍스트를 분석한 후 저자가 디오판토스가 아니라 디오판토스의 방법에 정통한 주석가, 아마도 히파티아일 가능성이 높다는 가설을 내놓았습니다.

Diophantus의 논문 "On Polygonal Numbers"(Περ? πολυγ?νΩν ?ριθμ?ν)는 완전히 보존되지 않았습니다. 보존된 부분에서는 기하학적 대수학 방법을 사용하여 여러 가지 보조 정리가 파생됩니다.

Diophantus의 "표면 측정"(?πιπεδομετρικ?) 및 "곱셈"(Περ? πολλαπλασιασμο?)의 작품에서도 단편 만 보존되었습니다.

Diophantus의 책 "Porisms"는 산술에서 사용되는 몇 가지 정리로만 알려져 있습니다.

오늘 방정식은 다음과 같은 형식입니다.

어디 피- 정수 함수(예: 정수 계수가 있는 다항식) 및 변수는 고대 그리스 수학자인 디오판틴(Diophantine)을 기리기 위해 정수 값을 취합니다.

아마도 가장 유명한 디오판토스 방정식은 다음과 같습니다.

그 해는 피타고라스의 삼중항입니다: (3; 4; 5), (6; 8; 10), (5; 12; 13), (12; 35; 37)…

디오판토스 방정식의 정수로 풀 수 없음 증명

~에 페르마의 마지막 정리(Fermat's Last Theorem)는 1994년 영국 수학자 앤드루 와일스(Andrew Wiles)가 완성했습니다.

Diophantine 방정식의 또 다른 예는 Pell의 방정식입니다.

매개변수는 어디에 있나요? N정확한 정사각형이 아닙니다.

힐베르트의 열 번째 문제는 데이비드 힐베르트가 1900년 8월 8일 제2차 국제 수학자 회의에서 제안한 23개의 문제 중 하나입니다. 힐베르트의 보고서에서 열 번째 문제의 공식화는 모든 문제 중 가장 짧습니다.

임의의 미지수와 정수 유리수 계수를 갖는 디오판토스 방정식이 주어집니다. 유한한 수의 연산 후에 이 방정식이 유리수로 풀 수 있는지 여부를 결정하는 것이 가능한 방법을 나타냅니다.

이 문제의 알고리즘적 해결 불가능성을 증명하는 데는 약 20년이 걸렸으며 1970년 Yuri Matiyasevich에 의해 완료되었습니다.

알렉산드리아의 파푸스(3세기)의 활동 덕분에 고대 과학자와 그들의 연구에 대한 정보가 우리에게 전해졌습니다. Apollonius (기원전 2세기부터) 이후 고대 과학의 쇠퇴가 시작되었습니다. 새로운 깊은 아이디어가 나타나지 않습니다. 기원전 146년. 이자형. 로마는 그리스를 점령하고 기원전 31년에 점령합니다. 이자형. - 알렉산드리아. 전반적인 침체와 쇠퇴를 배경으로 고대 고대 수학자 중 마지막이자 '대수학의 아버지'인 알렉산드리아의 디오판투스의 거대한 인물이 뚜렷하게 눈에 띕니다.

다음 수학적 개체는 Diophantus의 이름을 따서 명명되었습니다.