hjem › elektrisk utstyr › Multiplikasjon av brøker regel og eksempler. Multiplikasjon av enkle og blandede brøker med forskjellige nevnere

Multiplikasjon av brøker regel og eksempler. Multiplikasjon av enkle og blandede brøker med forskjellige nevnere

OMKAST DISSE RAKEN ALLEREDE! 🙂

Multiplikasjon og deling av brøker.

Merk følgende!
Det er flere
materiale i spesialseksjon 555.
For de som er sterke "ikke veldig. »
Og for de som «veldig jevn. "")

Denne operasjonen er mye bedre enn addisjon-subtraksjon! Fordi det er lettere. Jeg minner deg om: for å multiplisere en brøk med en brøk, må du multiplisere tellerne (dette vil være telleren for resultatet) og nevnerne (dette vil være nevneren). Det er:

Alt er ekstremt enkelt. Og vær så snill, ikke se etter en fellesnevner! Trenger det ikke her...

For å dele en brøk på en brøk, må du snu sekund(dette er viktig!) brøk og gang dem, dvs.:

Hvis multiplikasjon eller divisjon med heltall og brøker fanges opp, er det greit. Som med addisjon lager vi en brøk fra et helt tall med en enhet i nevneren - og går! For eksempel:

På videregående må du ofte forholde deg til tre-etasjers (eller til og med fire-etasjers!) brøker. For eksempel:

Hvordan bringe denne brøken til en anstendig form? Ja, veldig enkelt! Bruk divisjon gjennom to punkter:

Men ikke glem delingsrekkefølgen! I motsetning til multiplikasjon er dette veldig viktig her! Selvfølgelig skal vi ikke forveksle 4:2 eller 2:4. Men i en tre-etasjers brøk er det lett å gjøre feil. Vær for eksempel oppmerksom på:

I det første tilfellet (uttrykket til venstre):

I det andre (uttrykket til høyre):

Føl forskjellen? 4 og 1/9!

Hva er rekkefølgen på delingen? Eller parentes, eller (som her) lengden på horisontale streker. Utvikle et øye. Og hvis det ikke er noen parenteser eller bindestreker, som:

deretter dividere-multipliser i rekkefølge, venstre til høyre!

Og et annet veldig enkelt og viktig triks. I aksjoner med grader vil det komme godt med for deg! La oss dele enheten med en hvilken som helst brøk, for eksempel med 13/15:

Skuddet har snudd! Og det skjer alltid. Når du deler 1 med en hvilken som helst brøk, er resultatet den samme brøken, bare invertert.

Det er alle handlingene med brøker. Saken er ganske enkel, men gir mer enn nok feil. Merk praktiske råd, og de (feil) blir færre!

1. Det viktigste når du jobber med brøkuttrykk er nøyaktighet og oppmerksomhet! Dette er ikke vanlige ord, ikke gode ønsker! Dette er et alvorlig behov! Gjør alle beregningene på eksamen som en fullverdig oppgave, med konsentrasjon og klarhet. Det er bedre å skrive to ekstra linjer i et utkast enn å rote til når du regner i hodet.

2. I eksemplene med forskjellige typer brøker - gå til vanlige brøker.

3. Vi reduserer alle brøker til stopp.

4. Vi reduserer brøkuttrykk på flere nivåer til vanlige ved å bruke divisjon gjennom to punkter (vi følger divisjonsrekkefølgen!).

Her er oppgavene du må fullføre. Svar gis etter alle oppgaver. Bruk materialene til dette emnet og praktiske råd. Anslå hvor mange eksempler du kan løse riktig. Den første gangen! Uten kalkulator! Og trekke de riktige konklusjonene.

Husk riktig svar hentet fra andre (spesielt tredje) gang - teller ikke! Slik er det harde livet.

Så, løse i eksamensmodus ! Dette er forberedelse til eksamen, forresten. Vi løser et eksempel, vi sjekker, vi løser følgende. Vi bestemte alt - vi sjekket igjen fra første til siste. Men bare Deretter se på svarene.

Ser etter svar som matcher ditt. Jeg skrev dem med vilje ned i et rot, vekk fra fristelser, for å si det sånn. Her er de, svarene, atskilt med semikolon.

0; 17/22; 3/4; 2/5; 1; 25.

Og nå trekker vi konklusjoner. Hvis alt ordnet seg - glad i deg! Elementære beregninger med brøker er ikke ditt problem! Du kan gjøre mer alvorlige ting. Hvis ikke.

Så du har ett av to problemer. Eller begge deler på en gang.) Mangel på kunnskap og (eller) uoppmerksomhet. Men. Dette løselig Problemer.

I Special Section 555 "Fraksjoner" analyseres alle disse (og ikke bare!) eksemplene. Med detaljerte forklaringer på hva, hvorfor og hvordan. En slik analyse hjelper mye med mangel på kunnskap og ferdigheter!

Ja, og på det andre problemet er det noe der.) Ganske praktiske råd, hvordan bli mer oppmerksom. Ja Ja! Råd som kan gjelde hver.

I tillegg til kunnskap og oppmerksomhet, trengs en viss automatikk for å lykkes. Hvor får man tak i det? Jeg hører et tungt sukk... Ja, bare i praksis, ingen andre steder.

Du kan gå til nettstedet 321start.ru for trening. Der, i «Prøv»-alternativet, er det 10 eksempler som alle kan bruke. Med umiddelbar verifisering. For registrerte brukere - 34 eksempler fra enkle til alvorlige. Det er bare for brøkdeler.

Hvis du liker denne siden.

Forresten, jeg har et par flere interessante nettsteder for deg.)

Her kan du trene på å løse eksempler og finne ut ditt nivå. Testing med umiddelbar verifisering. Lær med interesse!

Og her kan du bli kjent med funksjoner og deriverte.

Regel 1

For å multiplisere en brøk med et naturlig tall, må du multiplisere telleren med dette tallet, og la nevneren være uendret.

Regel 2

For å multiplisere en brøk med en brøk:

1. finn produktet av tellerne og produktet av nevnerne til disse brøkene

2. Skriv det første produktet som teller, og det andre som nevner.

Regel 3

For å multiplisere blandede tall, må du skrive dem som uekte brøker, og deretter bruke regelen for å multiplisere brøker.

Regel 4

For å dele en brøk med en annen, må du multiplisere utbyttet med den gjensidige av divisoren.

Eksempel 1

Regne ut

Eksempel 2

Regne ut

Eksempel 3

Regne ut

Eksempel 4

Regne ut

Matematikk. Andre materialer

Å heve et tall til en rasjonell makt. (

Heve et tall til en naturlig kraft. (

Generalisert intervallmetode for å løse algebraiske ulikheter (forfatter Kolchanov A.V.)

Metode for erstatning av faktorer for å løse algebraiske ulikheter (forfatter Kolchanov A.V.)

Tegn på delbarhet (Lungu Alena)

Test deg selv på emnet 'Multiplikasjon og deling av vanlige brøker'

Multiplikasjon av brøker

Vi vil vurdere multiplikasjonen av vanlige brøker på flere mulige måter.

Å multiplisere en brøk med en brøk

Dette er det enkleste tilfellet, der du må bruke følgende brøkmultiplikasjonsregler.

Til multipliser en brøk med en brøk, nødvendig:

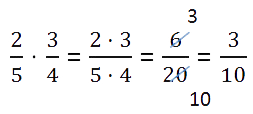
multipliser telleren til den første brøken med telleren til den andre brøken og skriv produktet deres inn i telleren til den nye brøken;

multipliser nevneren til den første brøken med nevneren til den andre brøken og skriv produktet inn i nevneren til den nye brøken;

Før du multipliserer tellere og nevnere, sjekk om brøkene kan reduseres. Å redusere brøker i beregninger vil i stor grad lette beregningene dine.

Multiplisere en brøk med et naturlig tall

Til brøk multiplisere med et naturlig tall du må gange telleren for brøken med dette tallet, og la brøkens nevner være uendret.

Hvis resultatet av multiplikasjon er en uekte brøk, ikke glem å gjøre det om til et blandet tall, det vil si, velg hele delen.

Multiplikasjon av blandede tall

For å multiplisere blandede tall, må du først konvertere dem til uekte brøker og deretter multiplisere i henhold til regelen for å multiplisere vanlige brøker.

En annen måte å multiplisere en brøk med et naturlig tall

Noen ganger i beregninger er det mer praktisk å bruke en annen metode for å multiplisere en vanlig brøk med et tall.

For å multiplisere en brøk med et naturlig tall, må du dele nevneren til brøken på dette tallet, og la telleren være den samme.

Som man kan se fra eksempelet, er det mer praktisk å bruke denne versjonen av regelen hvis nevneren til brøken er delelig uten en rest med et naturlig tall.

Divisjon av en brøk med et tall

Hva er den raskeste måten å dele en brøk på et tall? La oss analysere teorien, trekke en konklusjon og bruke eksempler for å se hvordan delingen av en brøk med et tall kan utføres etter en ny kortregel.

Vanligvis utføres delingen av en brøk med et tall i henhold til regelen for deling av brøker. Det første tallet (brøken) multipliseres med det resiproke av det andre. Siden det andre tallet er et heltall, er dets gjensidige en brøk, hvis teller er lik én, og nevneren er gitt nummer. Skjematisk ser det slik ut å dele en brøk med et naturlig tall:

Av dette konkluderer vi:

For å dele en brøk på et tall, multipliser nevneren med det tallet og la telleren være den samme. Regelen kan formuleres enda kortere:

Når du deler en brøk på et tall, går tallet til nevneren.

Del en brøk med et tall:

For å dele en brøk på et tall, omskriver vi telleren uendret, og multipliserer nevneren med dette tallet. Vi reduserer 6 og 3 med 3.

Når vi deler en brøk på et tall, skriver vi om telleren og multipliserer nevneren med det tallet. Vi reduserer 16 og 24 med 8.

Når du deler en brøk på et tall, går tallet til nevneren, så vi lar telleren være det samme, og ganger nevneren med divisor. Vi reduserer 21 og 35 med 7.

Multiplikasjon og deling av brøker

Forrige gang lærte vi å legge til og subtrahere brøker (se leksjonen "Legge til og trekke fra brøker"). Det vanskeligste øyeblikket i disse handlingene var å bringe brøker til en fellesnevner.

Nå er det på tide å håndtere multiplikasjon og divisjon. Den gode nyheten er at disse operasjonene er enda enklere enn addisjon og subtraksjon. For å begynne, vurder enkleste tilfelle, når det er to positive brøker uten en distingvert heltallsdel.

For å multiplisere to brøker, må du multiplisere deres tellere og nevnere hver for seg. Det første tallet vil være telleren til den nye brøken, og det andre vil være nevneren.

For å dele to brøker, må du multiplisere den første brøken med den "inverterte" andre.

Av definisjonen følger det at deling av brøker reduseres til multiplikasjon. For å snu en brøk, bytt bare teller og nevner. Derfor vil hele leksjonen hovedsakelig vurdere multiplikasjon.

Som et resultat av multiplikasjon kan en redusert brøk oppstå (og ofte oppstår det) - selvfølgelig må den reduseres. Hvis brøken etter alle reduksjonene viste seg å være feil, bør hele delen skilles ut i den. Men det som akkurat ikke vil skje med multiplikasjon er reduksjon til en fellesnevner: ingen kryssmetoder, maksimumsfaktorer og minst felles multiplum.

Oppgave. Finn verdien av uttrykket:

Per definisjon har vi:

Multiplikasjon av brøker med en heltallsdel og negative brøker

Hvis det er en heltallsdel i brøkene, må de konverteres til upassende - og først deretter multipliseres i henhold til skjemaene som er skissert ovenfor.

Hvis det er et minus i telleren til en brøk, i nevneren eller foran den, kan den tas ut av multiplikasjonsgrensene eller fjernes helt i henhold til følgende regler:

Pluss ganger minus gir minus;
To negative gir en bekreftende.

Til nå har disse reglene kun vært påtruffet når man legger til og subtraherer negative brøker, da det var nødvendig for å bli kvitt hele delen. For et produkt kan de generaliseres for å "brenne" flere minuser samtidig:

Vi krysser ut minusene i par til de forsvinner helt. I et ekstremt tilfelle kan ett minus overleve - den som ikke fant en match;
Hvis det ikke er noen minuser igjen, er operasjonen fullført - du kan begynne å multiplisere. Hvis det siste minuset ikke er krysset ut, siden det ikke fant et par, tar vi det ut av multiplikasjonsgrensene. Du får en negativ brøkdel.

Vi oversetter alle brøker til uekte, og så tar vi ut minusene utenfor multiplikasjonsgrensene. Det som er igjen multipliseres med vanlige regler. Vi får:

La meg igjen minne om at minus som kommer foran en brøk med en uthevet heltallsdel refererer spesifikt til hele brøken, og ikke bare til dens heltallsdel (dette gjelder de to siste eksemplene).

Vær også oppmerksom på negative tall: når de multipliseres, er de omsluttet av parentes. Dette gjøres for å skille minusene fra multiplikasjonstegnene og gjøre hele notasjonen mer nøyaktig.

Reduserer fraksjoner i farten

Multiplikasjon er en svært arbeidskrevende operasjon. Tallene her er ganske store, og for å forenkle oppgaven kan du prøve å redusere brøken enda mer før multiplikasjon. Faktisk, i hovedsak er tellerne og nevnerne til brøker vanlige faktorer, og derfor kan de reduseres ved å bruke den grunnleggende egenskapen til en brøk. Ta en titt på eksemplene:

I alle eksemplene er tallene som er redusert og det som er igjen av dem markert med rødt.

Vær oppmerksom på: i det første tilfellet ble multiplikatorene redusert fullstendig. Enheter forble på sin plass, som generelt sett kan utelates. I det andre eksemplet full reduksjon det var ikke mulig å oppnå, men den totale mengden beregninger gikk likevel ned.

Ikke bruk i noe tilfelle denne teknikken når du legger til og subtraherer brøker! Ja, noen ganger er det lignende tall som du bare vil redusere. Her, se:

Det kan du ikke gjøre!

Feilen oppstår på grunn av at når du legger til en brøk, vises summen i telleren til en brøk, og ikke produktet av tall. Derfor er det umulig å bruke hovedegenskapen til en brøk, siden i denne egenskapen vi snakker Det handler om å multiplisere tall.

Det er rett og slett ingen annen grunn til å redusere brøker, så den riktige løsningen på det forrige problemet ser slik ut:

Som du kan se, viste det seg at det riktige svaret ikke var så vakkert. Generelt, vær forsiktig.

Inndeling av brøker.

Divisjon av en brøk med et naturlig tall.

Eksempler på å dele en brøk med et naturlig tall

Divisjon av et naturlig tall med en brøk.

Eksempler på å dele et naturlig tall med en brøk

Deling av vanlige brøker.

Eksempler på deling av vanlige brøker

Inndeling av blandede tall.

konvertere blandede fraksjoner til uekte;
multipliser den første brøken med den resiproke av den andre;
reduser den resulterende fraksjonen;
Hvis du får en uekte brøk, konverter den uekte brøken til en blandet.

Eksempler på å dele blandede tall

1 1 2: 2 2 3 = 1 2 + 1 2: 2 3 + 2 3 = 3 2: 8 3 = 3 2 3 8 = 3 3 2 8 = 9 16

2 1 7: 3 5 = 2 7 + 1 7: 3 5 = 15 7: 3 5 = 15 7 5 3 = 15 5 7 3 = 5 5 7 = 25 7 = 7 3 + 4 7 = 3 4 7

Eventuelle uanstendige kommentarer vil bli fjernet og forfatterne svartelistet!

Velkommen til OnlineMSschool.
Mitt navn er Dovzhik Mikhail Viktorovich. Jeg er eier og forfatter av dette nettstedet, jeg skrev hele teoretisk materiale, samt nettbaserte øvelser og kalkulatorer som du kan bruke til å studere matematikk.

Brøker. Multiplikasjon og deling av brøker.

Å multiplisere en brøk med en brøk.

For å multiplisere vanlige brøker, er det nødvendig å multiplisere telleren med telleren (vi får telleren til produktet) og nevneren med nevneren (vi får nevneren til produktet).

Formel for brøkmultiplikasjon:

Før du fortsetter med multiplikasjonen av tellere og nevnere, er det nødvendig å se etter muligheten for å redusere brøken. Klarer du å redusere brøken, så vil det være lettere for deg å fortsette å gjøre beregninger.

Merk! Det er ingen grunn til å lete etter en fellesnevner!!

Deling av en vanlig brøk med en brøk.

Delingen av en vanlig brøk med en brøk er som følger: snu den andre brøken (dvs. endre telleren og nevneren på steder) og deretter multipliseres brøkene.

Formelen for å dele vanlige brøker:

Multiplisere en brøk med et naturlig tall.

Merk! Når du multipliserer en brøk med et naturlig tall, multipliseres brøkens teller med vårt naturlige tall, og nevneren for brøken forblir den samme. Hvis resultatet av produktet er en upassende fraksjon, sørg for å velge hele delen ved å gjøre den upassende fraksjonen om til en blandet.

Divisjon av brøker som involverer et naturlig tall.

Det er ikke så skummelt som det virker. Som ved addisjon konverterer vi et heltall til en brøk med en enhet i nevneren. For eksempel:

Multiplikasjon av blandede brøker.

Regler for å multiplisere brøker (blandet):

konvertere blandede fraksjoner til uekte;
multipliser tellerne og nevnerne av brøker;
vi reduserer brøken;
hvis vi får en uekte brøk, så konverterer vi uekte brøk til en blandet.

Merk! For å multiplisere en blandet brøk med en annen blandet brøk, må du først bringe dem til form av uekte brøker, og deretter multiplisere i henhold til regelen for å multiplisere vanlige brøker.

Den andre måten å multiplisere en brøk med et naturlig tall.

Det er mer praktisk å bruke den andre metoden for å multiplisere en vanlig brøk med et tall.

Merk! For å multiplisere en brøk med et naturlig tall, er det nødvendig å dele nevneren til brøken med dette tallet, og la telleren være uendret.

Fra eksemplet ovenfor er det klart at dette alternativet er mer praktisk å bruke når nevneren til en brøk er delt uten en rest med et naturlig tall.

Flernivåbrøker.

På videregående finner man ofte tre-etasjers (eller flere) brøker. Eksempel:

For å bringe en slik brøk til sin vanlige form, brukes divisjon gjennom 2 poeng:

Merk! Ved deling av brøker er rekkefølgen på delingen svært viktig. Vær forsiktig, det er lett å bli forvirret her.

Merk, For eksempel:

Når du deler en med en hvilken som helst brøk, vil resultatet være den samme brøken, bare invertert:

Praktiske tips for å multiplisere og dele brøker:

1. Det viktigste i arbeidet med brøkuttrykk er nøyaktighet og oppmerksomhet. Gjør alle beregninger nøye og nøyaktig, konsentrert og tydelig. Det er bedre å skrive ned noen ekstra linjer i et utkast enn å bli forvirret i beregningene i hodet.

2. I oppgaver med ulike typer brøker, gå til typen vanlige brøker.

3. Vi reduserer alle brøker til det ikke lenger er mulig å redusere.

4. Vi bringer brøkuttrykk på flere nivåer inn i vanlige uttrykk ved å bruke divisjon gjennom 2 punkter.

Under- og ikke opp til- Omarbeidet sang "Vårtango" (Tiden kommer - fugler fra sør kommer) - musikk. Valery Milyaev Jeg hørte feil, jeg misforstod, jeg fanget ikke opp, i den forstand at jeg ikke gjettet, jeg skrev alle verbene med ikke separat, jeg visste ikke om prefikset nedo-. Det skjer, […]
Siden ble ikke funnet I den tredje siste lesingen ble en pakke med regjeringsdokumenter som sørger for opprettelse av spesielle administrative regioner (SAR) vedtatt. På grunn av utgangen fra EU vil ikke Storbritannia bli inkludert i det europeiske momsområdet og […]
Felles etterforskningskomité vil dukke opp til høsten
Et algoritmepatent Hvordan et algoritmepatent ser ut Hvordan et algoritmepatent blir utarbeidet tekniske beskrivelser måter å lagre, behandle og overføre signaler og/eller data spesifikt for patentering på byr vanligvis ikke på noen spesielle vanskeligheter, og […]
HVA ER VIKTIG Å VITE OM DET NYE UTKASTET TIL PENSJONER 12. desember 1993 KONSTITUSJONEN FOR DEN RUSSISKE FØDERASJONEN (med forbehold om endringer gjort av lovene i Den russiske føderasjonen om endringer i den russiske føderasjonens grunnlov datert 30. desember 2008 N 6-6 FKZ, datert 30. desember 2008 N 7-FKZ, […]
Ditties om pensjonering for en kvinne er kult for en manns dagens helt for en manns helt for dagen - i kor for en kvinnes helt for dagen - dedikasjon til pensjonerte kvinner er komisk Konkurranser for pensjonister vil være interessant kjære venner! Et øyeblikks oppmerksomhet! Følelse! Bare […]

I løpet av gjennomsnittet og videregående skole Elevene gikk gjennom temaet «Brøker». Dette konseptet er imidlertid mye bredere enn gitt i læringsprosessen. I dag møtes begrepet brøk ganske ofte, og ikke alle kan beregne noe uttrykk, for eksempel multiplisere brøker.

Hva er en brøk?

Det skjedde historisk at brøktall dukket opp på grunn av behovet for å måle. Som praksis viser, er det ofte eksempler på å bestemme lengden på et segment, volumet til et rektangulært rektangel.

I første omgang blir studentene introdusert for et slikt konsept som en andel. For eksempel, hvis du deler en vannmelon i 8 deler, vil hver få en åttendedel av en vannmelon. Denne ene delen av åtte kalles en andel.

En andel lik ½ av en hvilken som helst verdi kalles en halv; ⅓ - tredje; ¼ - en fjerdedel. Oppføringer som 5/8, 4/5, 2/4 kalles vanlige brøker. En vanlig brøk er delt inn i en teller og en nevner. Mellom dem er en brøklinje, eller brøklinje. En brøklinje kan tegnes enten som en horisontal eller en skrå linje. I denne saken det står for divisjonstegnet.

Nevneren representerer hvor mange like deler verdien, objektet er delt inn i; og telleren er hvor mange like deler som tas. Telleren skrives over brøkstreken, nevneren under den.

Det er mest praktisk å vise vanlige brøker på en koordinatstråle. Hvis et enkelt segment er delt inn i 4 like deler, utpek hver del latinsk bokstav, så som et resultat kan du få en utmerket visuelt materiale. Så, punkt A viser en andel lik 1/4 av hele enhetssegmentet, og punkt B markerer 2/8 av dette segmentet.

Varianter av brøker

Brøker er vanlige, desimale og blandede tall. I tillegg kan brøker deles inn i riktige og uekte. Denne klassifiseringen er mer egnet for vanlige fraksjoner.

En egenbrøk er et tall hvis teller er mindre enn nevneren. Følgelig er en uekte brøk et tall hvis teller er større enn nevneren. Den andre typen skrives vanligvis som et blandet tall. Et slikt uttrykk består av en heltallsdel og en brøkdel. For eksempel 1½. 1 - heltallsdel, ½ - brøk. Men hvis du trenger å utføre noen manipulasjoner med uttrykket (dele eller multiplisere brøker, redusere eller konvertere dem), konverteres det blandede tallet til en uekte brøk.

Et korrekt brøkuttrykk er alltid mindre enn én, og et uriktig uttrykk er alltid større enn eller lik 1.

Når det gjelder dette uttrykket, forstår de en post der et hvilket som helst tall er representert, hvor nevneren til brøkuttrykket kan uttrykkes gjennom en med flere nuller. Hvis brøken er riktig, vil heltallsdelen i desimalnotasjonen være null.

For å skrive en desimal må du først skrive heltallsdelen, skille den fra brøken med komma, og deretter skrive brøkuttrykket. Det må huskes at etter kommaet må telleren inneholde like mange numeriske tegn som det er null i nevneren.

Eksempel. Representer brøken 7 21 / 1000 i desimalnotasjon.

Algoritme for å konvertere en uekte brøk til et blandet tall og omvendt

Det er feil å skrive ned en uekte brøk i svaret på oppgaven, så den må konverteres til et blandet tall:

del telleren med den eksisterende nevneren;
V spesifikt eksempel ufullstendig kvotient - hel;
og resten er telleren til brøkdelen, mens nevneren forblir uendret.

Eksempel. Konverter uekte brøk til blandet tall: 47 / 5 .

Løsning. 47: 5. Den ufullstendige kvotienten er 9, resten = 2. Derfor er 47 / 5 = 9 2 / 5.

Noen ganger må du representere et blandet tall som en uekte brøk. Da må du bruke følgende algoritme:

heltallsdelen multipliseres med nevneren til brøkuttrykket;
det resulterende produktet legges til telleren;
resultatet skrives i telleren, nevneren forblir uendret.

Eksempel. Uttrykk tallet i blandet form som en uekte brøk: 9 8 / 10 .

Løsning. 9 x 10 + 8 = 90 + 8 = 98 er telleren.

Svar: 98 / 10.

Multiplikasjon av vanlige brøker

Du kan utføre ulike algebraiske operasjoner på vanlige brøker. For å multiplisere to tall, må du multiplisere telleren med telleren, og nevneren med nevneren. Videre multiplikasjon av brøker med ulike nevnere skiller seg ikke fra produktet av brøktall med samme nevnere.

Det hender at etter å ha funnet resultatet, må du redusere brøkdelen. Det er viktig å forenkle det resulterende uttrykket så mye som mulig. Det kan selvsagt ikke sies at en uekte brøk i svaret er en feil, men det er også vanskelig å kalle det riktig svar.

Eksempel. Finn produktet av to vanlige brøker: ½ og 20/18.

Som man kan se fra eksemplet, etter å ha funnet produktet, oppnås en reduserbar brøknotasjon. Både telleren og nevneren i dette tilfellet er delelig med 4, og resultatet er svaret 5/9.

Multiplisere desimalbrøker

Produktet av desimalbrøker er ganske forskjellig fra produktet av vanlige brøker i sitt prinsipp. Så å multiplisere brøker er som følger:

to desimalbrøker må skrives under hverandre slik at sifrene lengst til høyre er under hverandre;
du må multiplisere de skrevne tallene, til tross for kommaene, det vil si som naturlige tall;
tell antall sifre etter komma i hvert av tallene;
i resultatet oppnådd etter multiplikasjon, må du telle så mange digitale tegn til høyre som er inneholdt i summen i begge faktorene etter desimaltegn, og sette et skilletegn;
hvis det er færre sifre i produktet, så må det skrives så mange nuller foran dem for å dekke dette tallet, sett et komma og tilordne en heltallsdel lik null.

Eksempel. Regn ut produktet av to desimaler: 2,25 og 3,6.

Løsning.

Multiplikasjon av blandede brøker

For å beregne produktet av to blandede brøker, må du bruke regelen for å multiplisere brøker:

konvertere blandede tall til uekte brøker;
finne produktet av tellere;
finn produktet av nevnerne;
skriv ned resultatet;
forenkle uttrykket så mye som mulig.

Eksempel. Finn produktet av 4½ og 6 2/5.

Multiplisere et tall med en brøk (brøker med et tall)

I tillegg til å finne produktet av to brøker, blandede tall, er det oppgaver der du må gange med en brøk.

Så for å finne produktet av en desimalbrøk og et naturlig tall, trenger du:

skriv tallet under brøken slik at sifrene lengst til høyre står over hverandre;
finne arbeidet, til tross for komma;
i det oppnådde resultatet skiller du heltallsdelen fra brøkdelen ved å bruke komma, og teller til høyre antall tegn som er etter desimalpunktet i brøken.

Å multiplisere vanlig brøk ved et tall, bør du finne produktet av telleren og den naturlige faktoren. Hvis svaret er en reduserbar brøk, bør den konverteres.

Eksempel. Regn ut produktet av 5/8 og 12.

Løsning. 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.

Svar: 7 1 / 2.

Som du kan se fra forrige eksempel, var det nødvendig å redusere det resulterende resultatet og konvertere det ukorrekte brøkuttrykket til et blandet tall.

Også multiplikasjonen av brøker gjelder også for å finne produktet av et tall i blandet form og en naturlig faktor. For å multiplisere disse to tallene, bør du multiplisere heltallsdelen av den blandede faktoren med tallet, multiplisere telleren med samme verdi, og la nevneren være uendret. Om nødvendig må du forenkle resultatet så mye som mulig.

Eksempel. Finn produktet av 9 5 / 6 og 9.

Løsning. 9 5 / 6 x 9 \u003d 9 x 9 + (5 x 9) / 6 \u003d 81 + 45 / 6 \u003d 81 + 7 3 / 6 \u003d 88 1/2.

Svar: 88 1 / 2.

Multiplikasjon med faktorene 10, 100, 1000 eller 0,1; 0,01; 0,001

Følgende regel følger av forrige avsnitt. For å multiplisere en desimalbrøk med 10, 100, 1000, 10000 osv., må du flytte kommaet til høyre med så mange siffer som det er null i multiplikatoren etter ett.

Eksempel 1. Finn produktet av 0,065 og 1000.

Løsning. 0,065 x 1000 = 0065 = 65.

Svar: 65.

Eksempel 2. Finn produktet av 3.9 og 1000.

Løsning. 3,9 x 1000 = 3,900 x 1000 = 3900.

Svar: 3900.

Hvis du trenger å multiplisere et naturlig tall og 0,1; 0,01; 0,001; 0,0001 osv., bør du flytte kommaet til venstre i det resulterende produktet med så mange siffer som det er nuller før ett. Om nødvendig skrives et tilstrekkelig antall nuller foran et naturlig tall.

Eksempel 1. Finn produktet av 56 og 0,01.

Løsning. 56 x 0,01 = 0056 = 0,56.

Svar: 0,56.

Eksempel 2. Finn produktet av 4 og 0,001.

Løsning. 4 x 0,001 = 0004 = 0,004.

Svar: 0,004.

Så å finne produktet av forskjellige fraksjoner bør ikke forårsake vanskeligheter, bortsett fra kanskje beregningen av resultatet; I dette tilfellet kan du rett og slett ikke klare deg uten en kalkulator.

Leksjonens innhold

Legge til brøker med samme nevnere

Å legge til brøker er av to typer:

Legge til brøker med samme nevnere
Legge til brøker med forskjellige nevnere

La oss begynne med å legge til brøker med de samme nevnerne. Alt er enkelt her. For å legge til brøker med de samme nevnerne, må du legge til deres tellere, og la nevneren være uendret. La oss for eksempel legge til brøkene og . Vi legger til tellerne og lar nevneren være uendret:

Dette eksemplet kan lett forstås hvis vi tenker på en pizza som er delt i fire deler. Legger du pizza til pizza, får du pizza:

Eksempel 2 Legg til brøker og .

Svaret er en uekte brøk. Hvis slutten av oppgaven kommer, er det vanlig å kvitte seg med upassende brøker. For å bli kvitt en upassende brøkdel, må du velge hele delen i den. I vårt tilfelle tildeles heltallsdelen enkelt - to delt på to er lik en:

Dette eksemplet kan lett forstås hvis vi tenker på en pizza som er delt i to. Legger du til flere pizzaer til pizzaen, får du en hel pizza:

Eksempel 3. Legg til brøker og .

Igjen, legg til tellerne, og la nevneren være uendret:

Dette eksemplet kan lett forstås hvis vi tenker på en pizza som er delt i tre deler. Hvis du legger til flere pizzaer til pizza, får du pizza:

Eksempel 4 Finn verdien av et uttrykk

Dette eksemplet er løst på nøyaktig samme måte som de forrige. Tellerne må legges til og nevneren holdes uendret:

La oss prøve å skildre løsningen vår ved hjelp av et bilde. Legger du pizza til en pizza og legger til flere pizzaer, får du 1 hel pizza og flere pizzaer.

Som du kan se, er det ikke vanskelig å legge til brøker med de samme nevnerne. Det er nok å forstå følgende regler:

For å legge til brøker med samme nevner, må du legge til deres tellere, og la nevneren være uendret;

Legge til brøker med forskjellige nevnere

Nå skal vi lære å legge til brøker med forskjellige nevnere. Når du legger til brøker, må nevnerne til disse brøkene være de samme. Men de er ikke alltid like.

For eksempel kan brøker legges til fordi de har de samme nevnerne.

Men brøker kan ikke legges til på en gang, fordi disse brøkene har forskjellige nevnere. I slike tilfeller må brøker reduseres til samme (felles)nevner.

Det er flere måter å redusere brøker til samme nevner. I dag vil vi vurdere bare en av dem, siden resten av metodene kan virke kompliserte for en nybegynner.

Essensen av denne metoden ligger i det faktum at først (LCM) av nevnerne til begge brøkene søkes. Deretter divideres LCM med nevneren til den første brøken og den første tilleggsfaktoren oppnås. De gjør det samme med den andre brøken - LCM deles på nevneren til den andre brøken og den andre tilleggsfaktoren oppnås.

Deretter multipliseres tellerne og nevnerne til brøkene med tilleggsfaktorene deres. Som et resultat av disse handlingene blir brøker som hadde forskjellige nevnere til brøker som har samme nevner. Og vi vet allerede hvordan vi legger til slike brøker.

Eksempel 1. Legg til brøker og

Først og fremst finner vi det minste felles multiplum av nevnerne til begge brøkene. Nevneren til den første brøken er tallet 3, og nevneren til den andre brøken er tallet 2. Minste felles multiplum av disse tallene er 6

LCM (2 og 3) = 6

Nå tilbake til brøker og . Først deler vi LCM med nevneren til den første brøken og får den første tilleggsfaktoren. LCM er tallet 6, og nevneren til den første brøken er tallet 3. Del 6 med 3, vi får 2.

Det resulterende tallet 2 er den første tilleggsfaktoren. Vi skriver det ned til den første brøken. For å gjøre dette lager vi en liten skrå linje over brøken og skriver ned den funnet ekstra faktoren over den:

Vi gjør det samme med den andre brøken. Vi deler LCM med nevneren til den andre brøken og får den andre tilleggsfaktoren. LCM er tallet 6, og nevneren til den andre brøken er tallet 2. Del 6 med 2, vi får 3.

Det resulterende tallet 3 er den andre tilleggsfaktoren. Vi skriver det til den andre brøken. Igjen lager vi en liten skrå linje over den andre brøken og skriver den funnet tilleggsfaktoren over den:

Nå er vi klare til å legge til. Det gjenstår å multiplisere tellerne og nevnerne av brøker med deres tilleggsfaktorer:

Se nøye på hva vi har kommet til. Vi kom frem til at brøker som hadde forskjellige nevner ble til brøker som hadde samme nevner. Og vi vet allerede hvordan vi legger til slike brøker. La oss fullføre dette eksemplet til slutten:

Dermed slutter eksemplet. Å legge til viser det seg.

La oss prøve å skildre løsningen vår ved hjelp av et bilde. Legger du pizza til en pizza, får du en hel pizza og en annen sjettedel av en pizza:

Reduksjon av brøker til samme (felles)nevner kan også avbildes ved hjelp av et bilde. Ved å bringe brøkene og til en fellesnevner, får vi brøkene og . Disse to fraksjonene vil være representert av de samme skivene med pizza. Den eneste forskjellen vil være at de denne gangen deles i like deler (redusert til samme nevner).

Den første tegningen viser en brøk (fire stykker av seks) og det andre bildet viser en brøk (tre stykker av seks). Setter vi disse bitene sammen får vi (syv av seks). Denne brøken er feil, så vi har markert heltallsdelen i den. Resultatet ble (en hel pizza og en annen sjette pizza).

Merk at vi har malt gitt eksempel for detaljert. I utdanningsinstitusjoner det er ikke vanlig å skrive på en så detaljert måte. Du må raskt kunne finne LCM for både nevnerne og tilleggsfaktorene til dem, samt raskt multiplisere tilleggsfaktorene funnet med tellerne og nevnerne dine. Mens vi er på skolen, må vi skrive dette eksemplet som følger:

Men det er også baksiden medaljer. Hvis det ikke gjøres detaljerte notater på de første stadiene av å studere matematikk, så spørsmål av typen "Hvor kommer det tallet fra?", "Hvorfor blir brøker plutselig til helt andre brøker? «.

For å gjøre det enklere å legge til brøker med forskjellige nevnere, kan du bruke følgende trinnvise instruksjoner:

Finn LCM for nevnerne til brøker;
Del LCM med nevneren for hver brøk og få en ekstra multiplikator for hver brøk;
Multipliser tellerne og nevnerne til brøker med tilleggsfaktorene deres;
Legg til brøker som har samme nevnere;
Hvis svaret viste seg å være en upassende brøkdel, velg hele delen;

Eksempel 2 Finn verdien av et uttrykk .

La oss bruke instruksjonene ovenfor.

Trinn 1. Finn LCM for nevnerne til brøker

Finn LCM for nevnerne til begge brøkene. Nevnerne til brøkene er tallene 2, 3 og 4

Trinn 2. Del LCM med nevneren for hver brøk og få en ekstra multiplikator for hver brøk

Del LCM med nevneren til den første brøken. LCM er tallet 12, og nevneren til den første brøken er tallet 2. Del 12 med 2, vi får 6. Vi fikk den første tilleggsfaktoren 6. Vi skriver den over den første brøken:

Nå deler vi LCM med nevneren til den andre brøken. LCM er tallet 12, og nevneren til den andre brøken er tallet 3. Del 12 med 3, vi får 4. Vi fikk den andre tilleggsfaktoren 4. Vi skriver den over den andre brøken:

Nå deler vi LCM med nevneren til den tredje brøken. LCM er tallet 12, og nevneren til den tredje brøken er tallet 4. Del 12 med 4, vi får 3. Vi fikk den tredje tilleggsfaktoren 3. Vi skriver den over den tredje brøken:

Trinn 3. Multipliser tellerne og nevnerne for brøker med tilleggsfaktorene dine

Vi multipliserer tellerne og nevnerne med våre tilleggsfaktorer:

Trinn 4. Legg til brøker som har samme nevnere

Vi kom til den konklusjonen at brøker som hadde ulike nevnere ble til brøker som har samme (felles)nevnere. Det gjenstår å legge til disse brøkene. Legg sammen:

Addisjonen passet ikke på én linje, så vi flyttet det gjenværende uttrykket til neste linje. Dette er tillatt i matematikk. Når et uttrykk ikke passer på en linje, overføres det til neste linje, og det er nødvendig å sette et likhetstegn (=) på slutten av den første linjen og i begynnelsen av en ny linje. Likhetstegnet på den andre linjen indikerer at dette er en fortsettelse av uttrykket som var på den første linjen.

Trinn 5. Hvis svaret viste seg å være en upassende brøkdel, velg hele delen i den

Svaret vårt er en uekte brøkdel. Vi må skille ut hele delen av det. Vi fremhever:

Fikk svar

Subtraksjon av brøker med samme nevnere

Det er to typer brøksubtraksjon:

Subtraksjon av brøker med samme nevnere
Subtraksjon av brøker med ulike nevnere

La oss først lære hvordan du trekker fra brøker med de samme nevnerne. Alt er enkelt her. For å trekke en annen fra en brøk, må du trekke telleren til den andre brøken fra telleren til den første brøken, og la nevneren være den samme.

La oss for eksempel finne verdien av uttrykket . For å løse dette eksemplet er det nødvendig å trekke telleren til den andre brøken fra telleren til den første brøken, og la nevneren være uendret. La oss gjøre dette:

Dette eksemplet kan lett forstås hvis vi tenker på en pizza som er delt i fire deler. Hvis du kutter pizza fra en pizza, får du pizza:

Eksempel 2 Finn verdien av uttrykket.

Igjen, fra telleren til den første brøken, trekk fra telleren til den andre brøken, og la nevneren være uendret:

Dette eksemplet kan lett forstås hvis vi tenker på en pizza som er delt i tre deler. Hvis du kutter pizza fra en pizza, får du pizza:

Eksempel 3 Finn verdien av et uttrykk

Dette eksemplet er løst på nøyaktig samme måte som de forrige. Fra telleren til den første brøken må du trekke fra tellerne til de gjenværende brøkene:

Som du kan se, er det ikke noe komplisert i å trekke fra brøker med de samme nevnerne. Det er nok å forstå følgende regler:

For å subtrahere en annen fra en brøk, må du trekke fra telleren til den andre brøken fra telleren til den første brøken, og la nevneren være uendret;
Hvis svaret viste seg å være en upassende brøkdel, må du velge hele delen i den.

Subtraksjon av brøker med ulike nevnere

For eksempel kan en brøk trekkes fra en brøk, siden disse brøkene har de samme nevnerne. Men en brøk kan ikke trekkes fra en brøk, fordi disse brøkene har forskjellige nevnere. I slike tilfeller må brøker reduseres til samme (felles)nevner.

Fellesnevneren finnes etter samme prinsipp som vi brukte når vi adderte brøker med ulike nevnere. Først av alt, finn LCM for nevnerne til begge brøkene. Deretter divideres LCM med nevneren til den første brøken og den første tilleggsfaktoren oppnås, som skrives over den første brøken. På samme måte deles LCM med nevneren til den andre brøken og en andre tilleggsfaktor oppnås, som skrives over den andre brøken.

Brøkene multipliseres deretter med tilleggsfaktorene. Som et resultat av disse operasjonene blir brøker som hadde forskjellige nevnere til brøker som har samme nevner. Og vi vet allerede hvordan vi trekker fra slike brøker.

Eksempel 1 Finn verdien av et uttrykk:

Disse brøkene har forskjellige nevnere, så du må bringe dem til samme (felles) nevner.

Først finner vi LCM for nevnerne til begge brøkene. Nevneren til den første brøken er tallet 3, og nevneren til den andre brøken er tallet 4. Minste felles multiplum av disse tallene er 12

LCM (3 og 4) = 12

Nå tilbake til brøker og

La oss finne en tilleggsfaktor for den første brøken. For å gjøre dette deler vi LCM med nevneren til den første brøken. LCM er tallet 12, og nevneren til den første brøken er tallet 3. Del 12 på 3, vi får 4. Vi skriver de fire over den første brøken:

Vi gjør det samme med den andre brøken. Vi deler LCM med nevneren til den andre brøken. LCM er tallet 12, og nevneren til den andre brøken er tallet 4. Del 12 med 4, vi får 3. Skriv en trippel over den andre brøken:

Nå er vi klare for subtraksjon. Det gjenstår å multiplisere brøkene med deres tilleggsfaktorer:

Vi kom frem til at brøker som hadde forskjellige nevner ble til brøker som hadde samme nevner. Og vi vet allerede hvordan vi trekker fra slike brøker. La oss fullføre dette eksemplet til slutten:

Fikk svar

La oss prøve å skildre løsningen vår ved hjelp av et bilde. Hvis du kutter pizza fra en pizza, får du pizza.

Dette er den detaljerte versjonen av løsningen. Når vi er på skolen, må vi løse dette eksempelet på en kortere måte. En slik løsning vil se slik ut:

Reduksjon av brøker og til en fellesnevner kan også avbildes ved hjelp av et bilde. Ved å bringe disse brøkene til en fellesnevner, får vi brøkene og . Disse brøkene vil bli representert av de samme pizzaskivene, men denne gangen vil de bli delt inn i de samme brøkene (redusert til samme nevner):

Den første tegningen viser en brøk (åtte stykker av tolv), og det andre bildet viser en brøk (tre stykker av tolv). Ved å kutte av tre stykker fra åtte stykker får vi fem stykker av tolv. Brøken beskriver disse fem stykkene.

Eksempel 2 Finn verdien av et uttrykk

Disse brøkene har forskjellige nevnere, så du må først bringe dem til den samme (felles) nevneren.

Finn LCM for nevnerne til disse brøkene.

Nevnerne til brøkene er tallene 10, 3 og 5. Minste felles multiplum av disse tallene er 30

LCM(10; 3; 5) = 30

Nå finner vi tilleggsfaktorer for hver brøk. For å gjøre dette deler vi LCM med nevneren for hver brøk.

La oss finne en tilleggsfaktor for den første brøken. LCM er tallet 30, og nevneren til den første brøken er tallet 10. Del 30 med 10, vi får den første tilleggsfaktoren 3. Vi skriver den over den første brøken:

Nå finner vi en tilleggsfaktor for den andre brøken. Del LCM med nevneren til den andre brøken. LCM er tallet 30, og nevneren til den andre brøken er tallet 3. Del 30 med 3, vi får den andre tilleggsfaktoren 10. Vi skriver den over den andre brøken:

Nå finner vi en tilleggsfaktor for den tredje brøken. Del LCM med nevneren til den tredje brøken. LCM er tallet 30, og nevneren til den tredje brøken er tallet 5. Del 30 med 5, vi får den tredje tilleggsfaktoren 6. Vi skriver den over den tredje brøken:

Nå er alt klart for subtraksjon. Det gjenstår å multiplisere brøkene med deres tilleggsfaktorer:

Vi kom til den konklusjonen at brøker som hadde ulike nevnere ble til brøker som har samme (felles)nevnere. Og vi vet allerede hvordan vi trekker fra slike brøker. La oss avslutte dette eksemplet.

Fortsettelsen av eksemplet vil ikke passe på én linje, så vi flytter fortsettelsen til neste linje. Ikke glem likhetstegnet (=) på den nye linjen:

Svaret viste seg å være en riktig brøk, og alt ser ut til å passe oss, men det er for tungvint og stygt. Vi bør gjøre det enklere. Hva kan bli gjort? Du kan redusere denne brøkdelen.

For å redusere en brøk, må du dele telleren og nevneren med (gcd) tallene 20 og 30.

Så vi finner GCD for tallene 20 og 30:

Nå går vi tilbake til vårt eksempel og deler telleren og nevneren av brøken med den funnet GCD, det vil si med 10

Fikk svar

Multiplisere en brøk med et tall

For å multiplisere en brøk med et tall, må du multiplisere telleren til den gitte brøken med dette tallet, og la nevneren være den samme.

Eksempel 1. Multipliser brøken med tallet 1.

Multipliser telleren av brøken med tallet 1

Inngangen kan forstås som å ta halv 1 gang. For eksempel, hvis du tar pizza 1 gang, får du pizza

Fra multiplikasjonslovene vet vi at hvis multiplikanten og multiplikatoren byttes om, vil ikke produktet endres. Hvis uttrykket skrives som , vil produktet fortsatt være lik . Igjen fungerer regelen for å multiplisere et heltall og en brøk:

Denne oppføringen kan forstås som å ta halvparten av enheten. For eksempel, hvis det er 1 hel pizza og vi tar halvparten av den, vil vi ha pizza:

Eksempel 2. Finn verdien av et uttrykk

Multipliser telleren av brøken med 4

Svaret er en uekte brøk. La oss ta en hel del av det:

Uttrykket kan forstås som å ta to kvarter 4 ganger. Tar du for eksempel pizza 4 ganger, får du to hele pizzaer.

Og hvis vi bytter ut multiplikatoren og multiplikatoren på steder, får vi uttrykket. Det vil også være lik 2. Dette uttrykket kan forstås som å ta to pizzaer fra fire hele pizzaer:

Multiplikasjon av brøker

For å multiplisere brøker, må du multiplisere deres tellere og nevnere. Hvis svaret er en uekte brøkdel, må du velge hele delen i den.

Eksempel 1 Finn verdien av uttrykket.

Fikk svar. Det er ønskelig å redusere denne fraksjonen. Fraksjonen kan reduseres med 2. Da vil den endelige løsningen ha følgende form:

Uttrykket kan forstås som å ta en pizza fra en halv pizza. La oss si at vi har en halv pizza:

Hvordan ta to tredjedeler fra denne halvdelen? Først må du dele denne halvdelen i tre like deler:

Og ta to fra disse tre delene:

Vi henter pizza. Husk hvordan en pizza ser ut delt i tre deler:

En skive fra denne pizzaen og de to skivene vi tok vil ha samme dimensjoner:

Vi snakker med andre ord om samme pizzastørrelse. Derfor er verdien av uttrykket

Eksempel 2. Finn verdien av et uttrykk

Multipliser telleren til den første brøken med telleren til den andre brøken, og nevneren til den første brøken med nevneren til den andre brøken:

Svaret er en uekte brøk. La oss ta en hel del av det:

Eksempel 3 Finn verdien av et uttrykk

Multipliser telleren til den første brøken med telleren til den andre brøken, og nevneren til den første brøken med nevneren til den andre brøken:

Svaret viste seg å være en riktig brøk, men det vil være bra om det reduseres. For å redusere denne brøken må du dele telleren og nevneren til denne brøken med den største felles deler(gcd) nummer 105 og 450.

Så la oss finne GCD for tallene 105 og 450:

Nå deler vi telleren og nevneren for svaret vårt på GCD som vi nå har funnet, det vil si med 15

Representerer et heltall som en brøk

Ethvert heltall kan representeres som en brøk. For eksempel kan tallet 5 representeres som . Fra dette vil de fem ikke endre sin betydning, siden uttrykket betyr "tallet fem delt på en", og dette, som du vet, er lik fem:

Omvendt tall

Nå skal vi bli kjent med interessant emne i matematikk. Det kalles "omvendte tall".

Definisjon. Tilbake til nummeren er tallet som multiplisert meden gir en enhet.

La oss erstatte i denne definisjonen i stedet for en variabel en nummer 5 og prøv å lese definisjonen:

Tilbake til nummer 5 er tallet som multiplisert med 5 gir en enhet.

Er det mulig å finne et tall som, multiplisert med 5, gir ett? Det viser seg at du kan. La oss representere fem som en brøk:

Multipliser deretter denne brøken med seg selv, bare bytt om teller og nevner. Med andre ord, la oss multiplisere brøken med seg selv, bare invertert:

Hva blir resultatet av dette? Hvis vi fortsetter å løse dette eksemplet, får vi ett:

Dette betyr at inversen av tallet 5 er tallet, siden når 5 multipliseres med én, oppnås en.

Det gjensidige kan også finnes for et hvilket som helst annet heltall.

Du kan også finne den gjensidige for enhver annen brøk. For å gjøre dette er det nok å snu den.

Divisjon av en brøk med et tall

La oss si at vi har en halv pizza:

La oss dele det likt mellom to. Hvor mange pizzaer får hver?

Det kan sees at etter å ha delt halvparten av pizzaen, ble det oppnådd to like biter som hver utgjør en pizza. Så alle får en pizza.

Deling av brøker gjøres ved å bruke resiproke. Gjensidige lar deg erstatte divisjon med multiplikasjon.

For å dele en brøk med et tall, må du multiplisere denne brøken med den resiproke av divisor.

Ved å bruke denne regelen vil vi skrive ned delingen av vår halvdel av pizzaen i to deler.

Så du må dele brøken med tallet 2. Her er utbyttet en brøk og divisor er 2.

For å dele en brøk med tallet 2, må du multiplisere denne brøken med den resiproke av divisor 2. Den resiproke av divisor 2 er en brøk. Så du må gange med

Multiplikasjon og deling av brøker.

Merk følgende!
Det er flere
materiale i spesialseksjon 555.
For de som sterkt "ikke veldig..."
Og for de som "veldig mye...")

For eksempel:

Alt er ekstremt enkelt. Og vær så snill, ikke se etter en fellesnevner! Trenger det ikke her...

For å dele en brøk på en brøk, må du snu sekund(dette er viktig!) brøk og gang dem, dvs.:

For eksempel:

Hvis multiplikasjon eller divisjon med heltall og brøker fanges opp, er det greit. Som med addisjon lager vi en brøk fra et helt tall med en enhet i nevneren - og går! For eksempel:

På videregående må du ofte forholde deg til tre-etasjers (eller til og med fire-etasjers!) brøker. For eksempel:

Hvordan bringe denne brøken til en anstendig form? Ja, veldig enkelt! Bruk divisjon gjennom to punkter:

I det første tilfellet (uttrykket til venstre):

I det andre (uttrykket til høyre):

Føl forskjellen? 4 og 1/9!

Hva er rekkefølgen på delingen? Eller parentes, eller (som her) lengden på horisontale streker. Utvikle et øye. Og hvis det ikke er noen parenteser eller bindestreker, som:

deretter dividere-multipliser i rekkefølge, venstre til høyre!

Og et annet veldig enkelt og viktig triks. I aksjoner med grader vil det komme godt med for deg! La oss dele enheten med en hvilken som helst brøk, for eksempel med 13/15:

Skuddet har snudd! Og det skjer alltid. Når du deler 1 med en hvilken som helst brøk, er resultatet den samme brøken, bare invertert.

Det er alle handlingene med brøker. Saken er ganske enkel, men gir mer enn nok feil. Legg merke til praktiske råd, så blir det færre av dem (feil)!

Praktiske tips:

2. I eksempler med ulike typer brøker - gå til vanlige brøker.

3. Vi reduserer alle brøker til stopp.

4. Vi reduserer brøkuttrykk på flere nivåer til vanlige ved å bruke divisjon gjennom to punkter (vi følger divisjonsrekkefølgen!).

5. Vi deler enheten inn i en brøk i tankene våre, ganske enkelt ved å snu brøken.

Husk riktig svar hentet fra andre (spesielt tredje) gang - teller ikke! Slik er det harde livet.

Regne ut:

Bestemte du deg?

Ser etter svar som matcher ditt. Jeg skrev dem spesifikt ned i et rot, vekk fra fristelsen, for å si det sånn... Her er de, svarene, skrevet ned med semikolon.

0; 17/22; 3/4; 2/5; 1; 25.

Og nå trekker vi konklusjoner. Hvis alt ordnet seg - glad i deg! Elementære beregninger med brøker er ikke ditt problem! Du kan gjøre mer alvorlige ting. Hvis ikke...

Så du har ett av to problemer. Eller begge deler på en gang.) Mangel på kunnskap og (eller) uoppmerksomhet. Men dette løselig Problemer.

Hvis du liker denne siden...

Forresten, jeg har et par flere interessante nettsteder for deg.)

Du kan trene på å løse eksempler og finne ut nivået ditt. Testing med umiddelbar verifisering. Læring - med interesse!)

du kan bli kjent med funksjoner og deriverte.

Forrige gang lærte vi å legge til og trekke fra brøker (se leksjonen "Addisjon og subtraksjon av brøker"). Det vanskeligste øyeblikket i disse handlingene var å bringe brøker til en fellesnevner.

Nå er det på tide å håndtere multiplikasjon og divisjon. Den gode nyheten er at disse operasjonene er enda enklere enn addisjon og subtraksjon. Til å begynne med, vurder det enkleste tilfellet, når det er to positive brøker uten en utpreget heltallsdel.

For å multiplisere to brøker, må du multiplisere deres tellere og nevnere hver for seg. Det første tallet vil være telleren til den nye brøken, og det andre vil være nevneren.

For å dele to brøker, må du multiplisere den første brøken med den "inverterte" andre.

Betegnelse:

Av definisjonen følger det at deling av brøker reduseres til multiplikasjon. For å snu en brøk, bytt bare teller og nevner. Derfor vil hele leksjonen hovedsakelig vurdere multiplikasjon.

Per definisjon har vi:

Multiplikasjon av brøker med en heltallsdel og negative brøker

Hvis det er en heltallsdel i brøkene, må de konverteres til upassende - og først deretter multipliseres i henhold til skjemaene som er skissert ovenfor.

Hvis det er et minus i telleren til en brøk, i nevneren eller foran den, kan den tas ut av multiplikasjonsgrensene eller fjernes helt i henhold til følgende regler:

Pluss ganger minus gir minus;
To negative gir en bekreftende.

Vi krysser ut minusene i par til de forsvinner helt. I et ekstremt tilfelle kan ett minus overleve - den som ikke fant en match;
Hvis det ikke er noen minuser igjen, er operasjonen fullført - du kan begynne å multiplisere. Hvis det siste minuset ikke er krysset ut, siden det ikke fant et par, tar vi det ut av multiplikasjonsgrensene. Du får en negativ brøkdel.

Oppgave. Finn verdien av uttrykket:

Vi oversetter alle brøker til uekte, og så tar vi ut minusene utenfor multiplikasjonsgrensene. Det som gjenstår multipliseres etter vanlige regler. Vi får:

La meg igjen minne om at minus som kommer foran en brøk med en uthevet heltallsdel refererer spesifikt til hele brøken, og ikke bare til dens heltallsdel (dette gjelder de to siste eksemplene).

Vær også oppmerksom på negative tall: når de multipliseres, er de omsluttet av parentes. Dette gjøres for å skille minusene fra multiplikasjonstegnene og gjøre hele notasjonen mer nøyaktig.

Reduserer fraksjoner i farten

Oppgave. Finn verdien av uttrykket:

Per definisjon har vi:

I alle eksemplene er tallene som er redusert og det som er igjen av dem markert med rødt.

Vær oppmerksom på: i det første tilfellet ble multiplikatorene redusert fullstendig. Enheter forble på sin plass, som generelt sett kan utelates. I det andre eksemplet var det ikke mulig å oppnå en fullstendig reduksjon, men den totale mengden beregninger gikk likevel ned.

Ikke bruk i noe tilfelle denne teknikken når du legger til og subtraherer brøker! Ja, noen ganger er det lignende tall som du bare vil redusere. Her, se:

Det kan du ikke gjøre!

Feilen oppstår på grunn av at når du legger til en brøk, vises summen i telleren til en brøk, og ikke produktet av tall. Derfor er det umulig å bruke hovedegenskapen til en brøk, siden denne egenskapen spesifikt omhandler multiplikasjon av tall.

Det er rett og slett ingen annen grunn til å redusere brøker, så den riktige løsningen på det forrige problemet ser slik ut: