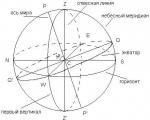
Wie schreibt man eine Lösung für ein Gleichungssystem? Systeme linearer Gleichungen

Anweisung

Additionsmethode.
Sie müssen zwei streng untereinander schreiben:

549+45y+4y=-7, 45y+4y=549-7, 49y=542, y=542:49, y≈11.
Fügen Sie in einer willkürlich gewählten (aus dem System) Gleichung die Zahl 11 anstelle des bereits gefundenen „Spiels“ ein und berechnen Sie die zweite Unbekannte:

X=61+5*11, x=61+55, x=116.
Die Antwort dieses Gleichungssystems: x=116, y=11.

Grafische Art und Weise.
Es besteht in der praktischen Ermittlung der Koordinaten des Punktes, an dem die Geraden mathematisch in das Gleichungssystem geschrieben werden. Sie sollten Diagramme beider Linien separat im selben Koordinatensystem zeichnen. Gesamtansicht: - y \u003d kx + b. Um eine Gerade zu konstruieren, reicht es aus, die Koordinaten zweier Punkte zu ermitteln, und x wird willkürlich gewählt.
Das System sei gegeben: 2x - y \u003d 4

Y \u003d -3x + 1.
Eine gerade Linie wird gemäß der ersten erstellt. Der Einfachheit halber muss sie aufgeschrieben werden: y \u003d 2x-4. Ermitteln Sie (einfachere) Werte für x, setzen Sie sie in die Gleichung ein, lösen Sie sie und finden Sie y. Man erhält zwei Punkte, entlang derer eine Gerade gebaut wird. (siehe Bild.)
x 0 1

y -4 -2
Eine Gerade wird nach der zweiten Gleichung konstruiert: y \u003d -3x + 1.
Bauen Sie auch eine Linie. (siehe Bild.)

1-5
Finden Sie die Koordinaten des Schnittpunkts zweier konstruierter Linien im Diagramm (wenn sich die Linien nicht schneiden, dann hat das Gleichungssystem keine - also).

Ähnliche Videos

Hilfreicher Rat

Wenn das gleiche Gleichungssystem durch drei gelöst wird verschiedene Wege, wird die Antwort dieselbe sein (wenn die Lösung richtig ist).

Quellen:

• Algebra Klasse 8
• Lösen Sie online eine Gleichung mit zwei Unbekannten
• Beispiele für die Lösung linearer Gleichungssysteme mit zwei

System Gleichungen ist eine Sammlung mathematischer Datensätze, von denen jeder eine bestimmte Anzahl von Variablen enthält. Es gibt mehrere Möglichkeiten, sie zu lösen.

Du wirst brauchen

• -Lineal und Bleistift;
• -Taschenrechner.

Anweisung

Betrachten Sie die Lösungssequenz des Systems, die aus linearen Gleichungen der Form besteht: a1x + b1y = c1 und a2x + b2y = c2. Dabei sind x und y unbekannte Variablen und b,c freie Mitglieder. Bei der Anwendung dieser Methode ist jedes System die Koordinaten der Punkte, die jeder Gleichung entsprechen. Drücken Sie zunächst jeweils eine Variable durch die andere aus. Setzen Sie dann die x-Variable auf eine beliebige Anzahl von Werten. Zwei reichen aus. Setzen Sie die Gleichung ein und finden Sie y. Erstellen Sie ein Koordinatensystem, markieren Sie darauf die erhaltenen Punkte und ziehen Sie eine gerade Linie durch sie. Ähnliche Berechnungen müssen für andere Teile des Systems durchgeführt werden.

Das System hat eine eindeutige Lösung, wenn sich die konstruierten Linien schneiden und eins gemeinsamer Punkt. Es ist inkonsistent, wenn sie parallel zueinander sind. Und es gibt unendlich viele Lösungen, wenn die Linien miteinander verschmelzen.

Diese Methode gilt als sehr übersichtlich. Der Hauptnachteil besteht darin, dass die berechneten Unbekannten Näherungswerte haben. Ein genaueres Ergebnis liefern die sogenannten algebraischen Methoden.

Jede Lösung eines Gleichungssystems ist es wert, überprüft zu werden. Ersetzen Sie dazu die erhaltenen Werte anstelle der Variablen. Sie können die Lösung auch auf verschiedene Arten finden. Wenn die Lösung des Systems richtig ist, sollten alle gleich ausfallen.

Oft gibt es Gleichungen, in denen einer der Terme unbekannt ist. Um eine Gleichung zu lösen, müssen Sie sich eine bestimmte Reihe von Aktionen mit diesen Zahlen merken und diese ausführen.

Du wirst brauchen

• - Blatt Papier;
• - Kugelschreiber oder Bleistift.

Anweisung

Stellen Sie sich vor, Sie haben 8 Kaninchen vor sich und nur 5 Karotten. Denken Sie, Sie müssen mehr Karotten kaufen, damit jedes Kaninchen eine Karotte bekommt.

Stellen wir dieses Problem in Form einer Gleichung dar: 5 + x = 8. Ersetzen wir x durch die Zahl 3. Tatsächlich ist 5 + 3 = 8.

Als Sie x durch eine Zahl ersetzten, führten Sie die gleiche Operation durch, als würden Sie 5 von 8 subtrahieren. Also finden Unbekannt Term: Subtrahieren Sie den bekannten Term von der Summe.

Nehmen wir an, Sie haben 20 Kaninchen und nur 5 Karotten. Lasst uns komponieren. Eine Gleichung ist eine Gleichheit, die nur für bestimmte Werte der darin enthaltenen Buchstaben gilt. Die Buchstaben, deren Werte Sie finden möchten, werden aufgerufen. Schreiben Sie eine Gleichung mit einer Unbekannten und nennen Sie sie x. Bei der Lösung unseres Kaninchenproblems erhält man die folgende Gleichung: 5 + x = 20.

Finden wir die Differenz zwischen 20 und 5. Beim Subtrahieren wird die Zahl, von der subtrahiert wird, reduziert. Die Zahl, die subtrahiert wird, heißt , und das Endergebnis heißt Differenz. Also, x = 20 - 5; x = 15. Sie müssen 15 Karotten für Kaninchen kaufen.

Überprüfen Sie: 5 + 15 = 20. Die Gleichung ist korrekt. Natürlich wann wir reden Bei so einfachen Fällen ist eine Überprüfung nicht erforderlich. Wenn es jedoch um Gleichungen mit dreistelligen, vierstelligen usw. geht, ist eine Überprüfung unbedingt erforderlich, um sich über das Ergebnis Ihrer Arbeit absolut sicher zu sein.

Ähnliche Videos

Hilfreicher Rat

Um den unbekannten Minuenden zu finden, müssen Sie den Subtrahend zur Differenz addieren.

Um den unbekannten Subtrahend zu finden, ist es notwendig, die Differenz vom Minuend zu subtrahieren.

Tipp 4: So lösen Sie ein System aus drei Gleichungen mit drei Unbekannten

Ein System aus drei Gleichungen mit drei Unbekannten kann trotz einer ausreichenden Anzahl von Gleichungen keine Lösungen haben. Sie können versuchen, es mit der Substitutionsmethode oder der Cramer-Methode zu lösen. Die Methode von Cramer ermöglicht nicht nur die Lösung des Systems, sondern auch die Bewertung, ob das System lösbar ist, bevor die Werte der Unbekannten ermittelt werden.

Anweisung

Die Substitutionsmethode besteht darin, nacheinander eine Unbekannte durch zwei andere zu ersetzen und das erhaltene Ergebnis in die Gleichungen des Systems einzusetzen. Gegeben sei ein System aus drei Gleichungen Gesamtansicht:

a1x + b1y + c1z = d1

a2x + b2y + c2z = d2

a3x + b3y + c3z = d3

Drücken Sie x aus der ersten Gleichung aus: x = (d1 - b1y - c1z)/a1 - und setzen Sie es in die zweite und dritte Gleichung ein. Drücken Sie dann y aus der zweiten Gleichung aus und setzen Sie es in die dritte ein. Sie erhalten einen linearen Ausdruck für z durch die Koeffizienten der Gleichungen des Systems. Gehen Sie nun „zurück“: Setzen Sie z in die zweite Gleichung ein und finden Sie y, setzen Sie dann z und y in die erste Gleichung ein und finden Sie x. Der Prozess ist im Allgemeinen in der Abbildung dargestellt, bis z gefunden wird. Darüber hinaus wird der Eintrag in allgemeiner Form zu umständlich sein. In der Praxis können Sie durch Ersetzen alle drei Unbekannten recht einfach finden.

Die Methode von Cramer besteht darin, die Matrix des Systems zusammenzustellen und die Determinante dieser Matrix sowie drei weitere Hilfsmatrizen zu berechnen. Die Matrix des Systems besteht aus den Koeffizienten an den unbekannten Termen der Gleichungen. Die Spalte mit den Zahlen auf der rechten Seite der Gleichungen, die Spalte auf der rechten Seite. Es wird nicht im System verwendet, sondern beim Lösen des Systems.

Ähnliche Videos

beachten Sie

Alle Gleichungen im System müssen unabhängig von anderen Gleichungen zusätzliche Informationen liefern. Andernfalls ist das System unterbestimmt und es kann keine eindeutige Lösung gefunden werden.

Hilfreicher Rat

Nachdem Sie das Gleichungssystem gelöst haben, setzen Sie die gefundenen Werte in das ursprüngliche System ein und prüfen Sie, ob sie alle Gleichungen erfüllen.

Von selbst Die gleichung mit drei Unbekannt hat viele Lösungen, daher wird es meistens durch zwei weitere Gleichungen oder Bedingungen ergänzt. Abhängig von den Ausgangsdaten wird der weitere Verlauf der Entscheidung maßgeblich abhängen.

Du wirst brauchen

• - ein System aus drei Gleichungen mit drei Unbekannten.

Anweisung

Wenn zwei der drei Systeme nur zwei der drei Unbekannten haben, versuchen Sie, einige Variablen durch die anderen auszudrücken und sie einzubinden Die gleichung mit drei Unbekannt. Ihr Ziel dabei ist es, daraus etwas Normales zu machen Die gleichung mit dem Unbekannten. Wenn dies der Fall ist, ist die weitere Lösung ganz einfach: Setzen Sie den gefundenen Wert in andere Gleichungen ein und finden Sie alle anderen Unbekannten.

Einige Gleichungssysteme können von einer Gleichung durch eine andere subtrahiert werden. Prüfen Sie, ob es möglich ist, eine davon mit oder einer Variablen zu multiplizieren, sodass zwei Unbekannte gleichzeitig reduziert werden. Wenn es eine solche Gelegenheit gibt, nutzen Sie sie höchstwahrscheinlich, die spätere Entscheidung wird Ihnen nicht schwer fallen. Vergessen Sie nicht, dass Sie beim Multiplizieren mit einer Zahl sowohl die linke als auch die rechte Seite multiplizieren müssen. Denken Sie auch beim Subtrahieren von Gleichungen daran, dass auch die rechte Seite subtrahiert werden muss.

Wenn bisherige Wege Hat nicht geholfen, verwenden Sie die allgemeine Methode zum Lösen von Gleichungen mit drei Unbekannt. Schreiben Sie dazu die Gleichungen in der Form a11x1 + a12x2 + a13x3 = b1, a21x1 + a22x2 + a23x3 = b2, a31x1 + a32x2 + a33x3 = b3 um. Erstellen Sie nun eine Matrix aus Koeffizienten bei x (A), eine Matrix aus Unbekannten (X) und eine Matrix aus freien Einsen (B). Beachten Sie, dass Sie durch Multiplizieren der Koeffizientenmatrix mit der Unbekanntenmatrix eine Matrix erhalten, eine Matrix freier Mitglieder, d. h. A * X \u003d B.

Finden Sie die Matrix A hoch (-1), nachdem Sie gefunden haben. Beachten Sie, dass sie nicht gleich Null sein sollte. Anschließend multiplizieren Sie die resultierende Matrix mit der Matrix B. Als Ergebnis erhalten Sie die gewünschte Matrix X, die alle Werte angibt.

Mit der Cramer-Methode können Sie auch eine Lösung für ein System aus drei Gleichungen finden. Finden Sie dazu die Determinante ∆ dritter Ordnung, die der Matrix des Systems entspricht. Finden Sie dann nacheinander drei weitere Determinanten ∆1, ∆2 und ∆3 und ersetzen Sie die Werte der freien Terme anstelle der Werte der entsprechenden Spalten. Finden Sie nun x: x1=∆1/∆, x2=∆2/∆, x3=∆3/∆.

Quellen:

• Lösungen von Gleichungen mit drei Unbekannten

Beginnen Sie mit der Lösung eines Gleichungssystems und finden Sie heraus, was diese Gleichungen sind. Die Methoden zur Lösung linearer Gleichungen sind gut untersucht. Nichtlineare Gleichungen werden meist nicht gelöst. Es gibt nur einen Sonderfall, der praktisch jeweils individuell ist. Daher sollte das Studium der Lösungsmethoden mit linearen Gleichungen beginnen. Solche Gleichungen können sogar rein algorithmisch gelöst werden.

Die Nenner der gefundenen Unbekannten sind genau gleich. Ja, und in den Zählern sind einige Muster ihrer Konstruktion sichtbar. Wenn die Dimension des Gleichungssystems größer als zwei wäre, würde die Eliminationsmethode zu sehr umständlichen Berechnungen führen. Um sie zu vermeiden, wurden rein algorithmische Lösungen entwickelt. Der einfachste davon ist der Cramer-Algorithmus (Cramer-Formeln). Denn Sie sollten es wissen allgemeines System Gleichungen aus n Gleichungen.

Das System aus n linearen algebraischen Gleichungen mit n Unbekannten hat die Form (siehe Abb. 1a). Darin sind aij die Koeffizienten des Systems,
хj – Unbekannte, bi – freie Mitglieder (i=1, 2, ... , n; j=1, 2, ... , n). Ein solches System kann kompakt in der Matrixform AX=B geschrieben werden. Dabei ist A die Koeffizientenmatrix des Systems, X die Spaltenmatrix der Unbekannten und B die Spaltenmatrix der freien Terme (siehe Abb. 1b). Nach der Methode von Cramer ist jedes Unbekannte xi =∆i/∆ (i=1,2…,n). Die Determinante ∆ der Koeffizientenmatrix wird als Hauptdeterminante und ∆i als Hilfsdeterminante bezeichnet. Für jede Unbekannte wird eine Hilfsdeterminante gefunden, indem die i-te Spalte der Hauptdeterminante durch eine Spalte mit freien Termen ersetzt wird. Cramers Methode für den Fall von Systemen zweiter und dritter Ordnung ist in Abb. detailliert dargestellt. 2.

Ein System ist eine Vereinigung von zwei oder mehr Gleichheiten, von denen jede zwei oder mehr Unbekannte hat. Es gibt zwei Hauptmethoden zur Lösung linearer Gleichungssysteme, die im Framework verwendet werden Lehrplan. Eine davon wird als Methode bezeichnet, die andere als Additionsmethode.

Standardform eines Systems aus zwei Gleichungen

Bei Standardform Die erste Gleichung ist a1*x+b1*y=c1, die zweite Gleichung ist a2*x+b2*y=c2 und so weiter. Beispielsweise sind im Fall von zwei Teilen des Systems in beiden gegebenen a1, a2, b1, b2, c1, c2 einige numerische Koeffizienten in spezifischen Gleichungen dargestellt. x und y wiederum sind Unbekannte, deren Werte bestimmt werden müssen. Die gewünschten Werte verwandeln beide Gleichungen gleichzeitig in echte Gleichheiten.

Lösung des Systems durch die Additionsmethode

Um das System zu lösen, also die Werte von x und y zu finden, die sie in echte Gleichheiten umwandeln, müssen Sie ein paar einfache Schritte unternehmen. Die erste davon besteht darin, eine der Gleichungen so umzuwandeln, dass die numerischen Koeffizienten für die Variable x oder y in beiden Gleichungen im Absolutwert übereinstimmen, sich jedoch im Vorzeichen unterscheiden.

Gegeben sei beispielsweise ein System bestehend aus zwei Gleichungen. Der erste davon hat die Form 2x+4y=8, der zweite die Form 6x+2y=6. Eine Möglichkeit, die Aufgabe zu lösen, besteht darin, die zweite Gleichung mit dem Faktor -2 zu multiplizieren, was zu der Form -12x-4y=-12 führt. Die richtige Wahl des Koeffizienten ist eine der Schlüsselaufgaben bei der Lösung des Systems nach der Additionsmethode, da sie den gesamten weiteren Ablauf des Verfahrens zum Auffinden von Unbekannten bestimmt.

Nun müssen die beiden Gleichungen des Systems addiert werden. Offensichtlich führt die gegenseitige Zerstörung von Variablen mit gleichem Wert, aber entgegengesetzten Vorzeichenkoeffizienten zu der Form -10x=-4. Danach muss diese einfache Gleichung gelöst werden, aus der eindeutig folgt, dass x=0,4.

Letzter Schritt Im Lösungsprozess wird der gefundene Wert einer der Variablen durch eine der im System verfügbaren Anfangsgleichungen ersetzt. Wenn Sie beispielsweise x=0,4 in die erste Gleichung einsetzen, erhalten Sie den Ausdruck 2*0,4+4y=8, woraus y=1,8 resultiert. Somit sind x=0,4 und y=1,8 die Wurzeln des im Beispiel gezeigten Systems.

Um sicherzustellen, dass die Wurzeln korrekt gefunden wurden, ist es sinnvoll, die gefundenen Werte durch Einsetzen in die zweite Gleichung des Systems zu überprüfen. Zum Beispiel in dieser Fall Man erhält eine Gleichheit der Form 0,4*6+1,8*2=6, was richtig ist.

Ähnliche Videos

Mit diesem mathematischen Programm können Sie ein System aus zwei linearen Gleichungen mit zwei Variablen mithilfe der Substitutionsmethode und der Additionsmethode lösen.

Das Programm gibt nicht nur die Antwort auf das Problem, sondern liefert auch eine detaillierte Lösung mit Erläuterungen zu den Lösungsschritten auf zwei Arten: der Substitutionsmethode und der Additionsmethode.

Dieses Programm kann für Oberstufenschüler nützlich sein allgemeinbildende Schulen in Vorbereitung für Kontrollarbeit und Prüfungen: Beim Testen von Wissen vor der Prüfung können Eltern die Lösung vieler Probleme in Mathematik und Algebra kontrollieren. Oder ist es für Sie vielleicht zu teuer, einen Nachhilfelehrer zu engagieren oder neue Lehrbücher zu kaufen? Oder möchten Sie es einfach so schnell wie möglich erledigen? Hausaufgaben Mathematik oder Algebra? In diesem Fall können Sie auch unsere Programme mit detaillierter Lösung nutzen.

So können Sie Ihre durchführen eigene Ausbildung und/oder Ausbildung ihrer jüngeren Geschwister, während gleichzeitig das Bildungsniveau im Bereich der zu lösenden Aufgaben erhöht wird.

Regeln für die Eingabe von Gleichungen

Als Variable kann jeder lateinische Buchstabe fungieren.
Zum Beispiel: \(x, y, z, a, b, c, o, p, q \) usw.

Bei der Eingabe von Gleichungen Sie können Klammern verwenden. In diesem Fall werden die Gleichungen zunächst vereinfacht. Die Gleichungen nach Vereinfachungen müssen linear sein, d.h. der Form ax+by+c=0 mit der Genauigkeit der Reihenfolge der Elemente.
Zum Beispiel: 6x+1 = 5(x+y)+2

In Gleichungen können Sie nicht nur ganze Zahlen, sondern auch Bruchzahlen in Form von Dezimal- und gewöhnlichen Brüchen verwenden.

Regeln für die Eingabe von Dezimalbrüchen.
Die ganzzahligen und gebrochenen Teile in Dezimalbrüchen können entweder durch einen Punkt oder ein Komma getrennt werden.
Zum Beispiel: 2,1n + 3,5m = 55

Regeln für die Eingabe gewöhnlicher Brüche.
Nur eine ganze Zahl kann als Zähler, Nenner und ganzzahliger Teil eines Bruchs fungieren.
Der Nenner darf nicht negativ sein.
Bei der Eingabe eines Zahlenbruchs wird der Zähler durch ein Divisionszeichen vom Nenner getrennt: /
Der ganzzahlige Teil wird durch ein kaufmännisches Und vom Bruch getrennt: &

Beispiele.
-1&2/3y + 5/3x = 55
2,1p + 55 = -2/7(3,5p - 2&1/8q)

Lösen Sie ein Gleichungssystem

Es wurde festgestellt, dass einige zur Lösung dieser Aufgabe benötigte Skripte nicht geladen wurden und das Programm möglicherweise nicht funktioniert.
Möglicherweise haben Sie AdBlock aktiviert.
Deaktivieren Sie es in diesem Fall und aktualisieren Sie die Seite.

Sie haben JavaScript in Ihrem Browser deaktiviert.
Damit die Lösung angezeigt wird, muss JavaScript aktiviert sein.
Hier finden Sie Anweisungen, wie Sie JavaScript in Ihrem Browser aktivieren.

Weil Es gibt viele Leute, die das Problem lösen möchten, Ihre Anfrage steht in der Warteschlange.
Nach ein paar Sekunden erscheint unten die Lösung.
Bitte warten Sie Sekunde...

Wenn Sie Habe einen Fehler in der Lösung bemerkt, dann können Sie im Feedback-Formular darüber schreiben.
Nicht vergessen Geben Sie an, um welche Aufgabe es sich handelt Du entscheidest was in die Felder eintragen.

Unsere Spiele, Rätsel, Emulatoren:

Ein bisschen Theorie.

Lösen linearer Gleichungssysteme. Substitutionsmethode

Die Abfolge der Aktionen beim Lösen eines linearen Gleichungssystems nach der Substitutionsmethode:
1) eine Variable aus einer Gleichung des Systems durch eine andere ausdrücken;
2) Ersetzen Sie den resultierenden Ausdruck anstelle dieser Variablen in einer anderen Gleichung des Systems.

$$ \left\( \begin(array)(l) 3x+y=7 \\ -5x+2y=3 \end(array) \right. $$

Lassen Sie uns aus der ersten Gleichung y bis x ausdrücken: y = 7-3x. Wenn wir den Ausdruck 7-3x anstelle von y in die zweite Gleichung einsetzen, erhalten wir das System:
$$ \left\( \begin(array)(l) y = 7-3x \\ -5x+2(7-3x)=3 \end(array) \right. $$

Es lässt sich leicht zeigen, dass das erste und das zweite System die gleichen Lösungen haben. Im zweiten System enthält die zweite Gleichung nur eine Variable. Lösen wir diese Gleichung:
$$ -5x+2(7-3x)=3 \Rightarrow -5x+14-6x=3 \Rightarrow -11x=-11 \Rightarrow x=1 $$

Wenn wir die Zahl 1 anstelle von x in die Gleichung y=7-3x einsetzen, finden wir den entsprechenden Wert von y:
$$ y=7-3 \cdot 1 \Rightarrow y=4 $$

Paar (1;4) - Lösung des Systems

Man nennt Gleichungssysteme in zwei Variablen, die die gleichen Lösungen haben Äquivalent. Als gleichwertig gelten auch Systeme, für die es keine Lösungen gibt.

Lösen linearer Gleichungssysteme durch Addition

Betrachten Sie eine andere Möglichkeit, lineare Gleichungssysteme zu lösen – die Additionsmethode. Bei der Lösung von Systemen auf diese Weise sowie bei der Lösung nach der Substitutionsmethode gehen wir von einem gegebenen System zu einem anderen äquivalenten System über, in dem eine der Gleichungen nur eine Variable enthält.

Die Abfolge der Aktionen beim Lösen eines linearen Gleichungssystems nach der Additionsmethode:
1) Multiplizieren Sie die Gleichungen des Systems Term für Term und wählen Sie Faktoren so aus, dass die Koeffizienten für eine der Variablen entgegengesetzte Zahlen werden;
2) Term für Term den linken und rechten Teil der Gleichungen des Systems hinzufügen;
3) Lösen Sie die resultierende Gleichung mit einer Variablen;
4) Finden Sie den entsprechenden Wert der zweiten Variablen.

Beispiel. Lösen wir das Gleichungssystem:
$$ \left\( \begin(array)(l) 2x+3y=-5 \\ x-3y=38 \end(array) \right. $$

In den Gleichungen dieses Systems sind die Koeffizienten von y entgegengesetzte Zahlen. Addiert man Term für Term den linken und rechten Teil der Gleichungen, erhält man eine Gleichung mit einer Variablen 3x=33. Ersetzen wir eine der Gleichungen des Systems, zum Beispiel die erste, durch die Gleichung 3x=33. Holen wir uns das System
$$ \left\( \begin(array)(l) 3x=33 \\ x-3y=38 \end(array) \right. $$

Aus der Gleichung 3x=33 finden wir, dass x=11. Wenn wir diesen x-Wert in die Gleichung \(x-3y=38 \) einsetzen, erhalten wir eine Gleichung mit der Variablen y: \(11-3y=38 \). Lösen wir diese Gleichung:
\(-3y=27 \Rightarrow y=-9 \)

Somit haben wir die Lösung des Gleichungssystems gefunden, indem wir Folgendes hinzugefügt haben: \(x=11; y=-9 \) oder \((11; -9) \)

Wir machten uns die Tatsache zunutze, dass die Koeffizienten von y in den Gleichungen des Systems entgegengesetzte Zahlen sind, und reduzierten seine Lösung auf die Lösung eines äquivalenten Systems (durch Summieren beider Teile jeder Gleichung des ursprünglichen Symmetrs), in dem man der Gleichungen enthält nur eine Variable.

Bücher (Lehrbücher) Zusammenfassungen des Einheitlichen Staatsexamens und der OGE-Tests online Spiele, Rätsel Konstruktion von Funktionsgraphen Rechtschreibwörterbuch der russischen Sprache Wörterbuch des Jugendslang Verzeichnis russischer Schulen Katalog weiterführender Schulen in Russland Katalog russischer Universitäten Aufgabenliste
Wir werden zwei Arten der Lösung von Gleichungssystemen analysieren:

1. Lösung des Systems durch die Substitutionsmethode.
2. Lösung des Systems durch termweise Addition (Subtraktion) der Gleichungen des Systems.

Um das Gleichungssystem zu lösen Substitutionsmethode Sie müssen einem einfachen Algorithmus folgen:
1. Wir drücken aus. Aus jeder Gleichung drücken wir eine Variable aus.
2. Ersatz. Wir ersetzen in einer anderen Gleichung anstelle der ausgedrückten Variablen den resultierenden Wert.
3. Wir lösen die resultierende Gleichung mit einer Variablen. Wir finden eine Lösung für das System.

Lösen System durch Term-für-Term-Addition (Subtraktion) müssen:
1. Wählen Sie eine Variable aus, für die wir die gleichen Koeffizienten erstellen.
2. Wir addieren oder subtrahieren die Gleichungen, als Ergebnis erhalten wir eine Gleichung mit einer Variablen.
3. Wir lösen die resultierende lineare Gleichung. Wir finden eine Lösung für das System.

Die Lösung des Systems sind die Schnittpunkte der Graphen der Funktion.

Betrachten wir die Lösung von Systemen anhand von Beispielen im Detail.

Beispiel 1:

Lassen Sie uns mit der Substitutionsmethode lösen

Lösen des Gleichungssystems mit der Substitutionsmethode

2x+5y=1 (1 Gleichung)
x-10y=3 (2. Gleichung)

1. Express
Es ist ersichtlich, dass es in der zweiten Gleichung eine Variable x mit einem Koeffizienten von 1 gibt, daher stellt sich heraus, dass es am einfachsten ist, die Variable x aus der zweiten Gleichung auszudrücken.
x=3+10y

2. Nach dem Ausdrücken ersetzen wir in der ersten Gleichung 3 + 10y anstelle der Variablen x.
2(3+10y)+5y=1

3. Wir lösen die resultierende Gleichung mit einer Variablen.
2(3+10y)+5y=1 (offene Klammern)
6+20J+5J=1
25 Jahre = 1–6
25y=-5 |: (25)
y=-5:25
y=-0,2

Die Lösung des Gleichungssystems sind die Schnittpunkte der Graphen, deshalb müssen wir x und y finden, weil der Schnittpunkt aus x und y besteht. Suchen wir x, im ersten Absatz, in dem wir es ausgedrückt haben, ersetzen wir dort y.
x=3+10y
x=3+10*(-0,2)=1

Es ist üblich, an erster Stelle Punkte zu schreiben, wir schreiben die Variable x und an zweiter Stelle die Variable y.
Antwort: (1; -0,2)

Beispiel #2:

Lassen Sie uns durch Term-für-Term-Addition (Subtraktion) lösen.

Lösen eines Gleichungssystems mit der Additionsmethode

3x-2y=1 (1 Gleichung)
2x-3y=-10 (2. Gleichung)

1. Wählen Sie eine Variable aus, sagen wir, wir wählen x aus. In der ersten Gleichung hat die Variable x einen Koeffizienten von 3, in der zweiten - 2. Wir müssen die Koeffizienten gleich machen, dafür haben wir das Recht, die Gleichungen zu multiplizieren oder durch eine beliebige Zahl zu dividieren. Wir multiplizieren die erste Gleichung mit 2 und die zweite mit 3 und erhalten einen Gesamtkoeffizienten von 6.

3x-2y=1 |*2
6x-4y=2

2x-3y=-10 |*3
6x-9y=-30

2. Subtrahieren Sie von der ersten Gleichung die zweite, um die Variable x zu entfernen. Lösen Sie die lineare Gleichung.
__6x-4y=2

5y=32 | :5
y=6,4

3. Finden Sie x. Wir ersetzen das gefundene y in einer der Gleichungen, sagen wir in der ersten Gleichung.
3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6

Der Schnittpunkt ist x=4,6; y=6,4
Antwort: (4.6; 6.4)

Möchten Sie sich kostenlos auf Prüfungen vorbereiten? Nachhilfe online kostenlos. Im Ernst.

Erinnern wir uns zunächst an die Definition einer Lösung eines Gleichungssystems in zwei Variablen.

Definition 1

Ein Zahlenpaar heißt Lösung eines Gleichungssystems mit zwei Variablen, wenn sich beim Einsetzen in die Gleichung die richtige Gleichheit ergibt.

Im Folgenden betrachten wir Systeme aus zwei Gleichungen mit zwei Variablen.

Existieren vier grundlegende Möglichkeiten, Gleichungssysteme zu lösen: Substitutionsmethode, Additionsmethode, grafische Methode, neue Variablenverwaltungsmethode. Werfen wir einen Blick auf diese Methoden konkrete Beispiele. Um das Prinzip der Verwendung der ersten drei Methoden zu beschreiben, betrachten wir ein System aus zwei linearen Gleichungen mit zwei Unbekannten:

Substitutionsmethode

Die Substitutionsmethode ist wie folgt: Eine dieser Gleichungen wird genommen und $y$ wird durch $x$ ausgedrückt, dann wird $y$ in die Gleichung des Systems eingesetzt, aus der die Variable $x.$ ermittelt wird. Danach können wir die Variable $y.$ leicht berechnen

Beispiel 1

Lassen Sie uns aus der zweiten Gleichung $y$ durch $x$ ausdrücken:

Setzen Sie in die erste Gleichung ein und finden Sie $x$:

\ \ \

Finden Sie $y$:

Antworten: $(-2,\ 3)$

Additionsmethode.

Betrachten Sie diese Methode anhand eines Beispiels:

Beispiel 2

\[\left\( \begin(array)(c) (2x+3y=5) \\ (3x-y=-9) \end(array) \right.\]

Multiplizieren Sie die zweite Gleichung mit 3, wir erhalten:

\[\left\( \begin(array)(c) (2x+3y=5) \\ (9x-3y=-27) \end(array) \right.\]

Nun addieren wir beide Gleichungen:

\ \ \

Finden Sie $y$ aus der zweiten Gleichung:

\[-6-y=-9\] \

Antworten: $(-2,\ 3)$

Bemerkung 1

Beachten Sie, dass bei dieser Methode eine oder beide Gleichungen mit solchen Zahlen multipliziert werden müssen, dass beim Hinzufügen eine der Variablen „verschwindet“.

Grafische Art und Weise

Die grafische Methode ist wie folgt: Beide Gleichungen des Systems werden auf der Koordinatenebene dargestellt und der Schnittpunkt ermittelt.

Beispiel 3

\[\left\( \begin(array)(c) (2x+3y=5) \\ (3x-y=-9) \end(array) \right.\]

Lassen Sie uns $y$ aus beiden Gleichungen durch $x$ ausdrücken:

\[\left\( \begin(array)(c) (y=\frac(5-2x)(3)) \\ (y=3x+9) \end(array) \right.\]

Zeichnen wir beide Graphen auf derselben Ebene:

Bild 1.

Antworten: $(-2,\ 3)$

So führen Sie neue Variablen ein

Wir betrachten diese Methode im folgenden Beispiel:

Beispiel 4

\[\left\( \begin(array)(c) (2^(x+1)-3^y=-1) \\ (3^y-2^x=2) \end(array) \right .\]

Lösung.

Dieses System entspricht dem System

\[\left\( \begin(array)(c) ((2\cdot 2)^x-3^y=-1) \\ (3^y-2^x=2) \end(array) \ Rechts.\]

Sei $2^x=u\ (u>0)$ und $3^y=v\ (v>0)$, wir erhalten:

\[\left\( \begin(array)(c) (2u-v=-1) \\ (v-u=2) \end(array) \right.\]

Wir lösen das resultierende System mit der Additionsmethode. Fügen wir die Gleichungen hinzu:

\ \

Dann erhalten wir das aus der zweiten Gleichung

Zurück zur Substitution erhalten wir neues System Exponentialgleichungen:

\[\left\( \begin(array)(c) (2^x=1) \\ (3^y=3) \end(array) \right.\]

Wir bekommen:

\[\left\( \begin(array)(c) (x=0) \\ (y=1) \end(array) \right.\]

Unterrichtsinhalte

Lineare Gleichungen mit zwei Variablen

Der Schüler hat 200 Rubel, um in der Schule zu Mittag zu essen. Ein Kuchen kostet 25 Rubel und eine Tasse Kaffee kostet 10 Rubel. Wie viele Kuchen und Tassen Kaffee kann man für 200 Rubel kaufen?

Geben Sie die Anzahl der Kuchen an X, und die Anzahl der Tassen Kaffee durch j. Dann werden die Kosten für Kuchen mit dem Ausdruck 25 bezeichnet X und die Kosten für Kaffeetassen in 10 j .

25X- Preis X Kuchen
10y- Preis j Tassen Kaffee

Der Gesamtbetrag sollte 200 Rubel betragen. Dann erhalten wir eine Gleichung mit zwei Variablen X Und j

25X+ 10j= 200

Wie viele Wurzeln hat diese Gleichung?

Es hängt alles vom Appetit des Schülers ab. Wenn er 6 Kuchen und 5 Tassen Kaffee kauft, sind die Wurzeln der Gleichung die Zahlen 6 und 5.

Das Wertepaar 6 und 5 soll die Wurzeln der Gleichung 25 sein X+ 10j= 200 . Geschrieben als (6; 5), wobei die erste Zahl der Wert der Variablen ist X und der zweite - der Wert der Variablen j .

6 und 5 sind nicht die einzigen Wurzeln, die Gleichung 25 umkehren X+ 10j= 200 zur Identität. Auf Wunsch kann ein Student für die gleichen 200 Rubel 4 Kuchen und 10 Tassen Kaffee kaufen:

In diesem Fall sind die Wurzeln der Gleichung 25 X+ 10j= 200 ist das Wertepaar (4; 10).

Außerdem darf ein Student überhaupt keinen Kaffee kaufen, dafür aber Kuchen für ganze 200 Rubel. Dann sind die Wurzeln der Gleichung 25 X+ 10j= 200 werden die Werte 8 und 0 sein

Oder umgekehrt: Kaufen Sie keine Kuchen, sondern Kaffee für alle 200 Rubel. Dann sind die Wurzeln der Gleichung 25 X+ 10j= 200 werden die Werte 0 und 20 sein

Versuchen wir, alle möglichen Wurzeln der Gleichung 25 aufzulisten X+ 10j= 200 . Lassen Sie uns die Werte vereinbaren X Und j gehören zur Menge der ganzen Zahlen. Und seien diese Werte größer oder gleich Null:

X∈Z, y∈ Z;
x ≥ 0, y ≥ 0

So ist es für den Schüler selbst praktisch. Kuchen lassen sich bequemer im Ganzen kaufen als beispielsweise mehrere ganze Kuchen und einen halben Kuchen. Kaffee lässt sich auch bequemer in ganzen Tassen einnehmen als beispielsweise mehrere ganze Tassen und eine halbe Tasse.

Beachten Sie das für ungerade X Es ist unmöglich, Gleichheit unter allen zu erreichen j. Dann die Werte X Es wird die folgenden Zahlen geben: 0, 2, 4, 6, 8. Und wissend X lässt sich leicht ermitteln j

Somit haben wir die folgenden Wertepaare erhalten (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Diese Paare sind Lösungen oder Wurzeln von Gleichung 25 X+ 10j= 200. Sie verwandeln diese Gleichung in eine Identität.

Typgleichung Axt + by = c genannt lineare Gleichung mit zwei Variablen. Eine Lösung oder Wurzeln dieser Gleichung ist ein Wertepaar ( X; j), was daraus eine Identität macht.

Beachten Sie auch, dass eine lineare Gleichung mit zwei Variablen wie folgt geschrieben wird: ax + by = c , dann sagen sie, dass es geschrieben steht kanonisch(Normal-)Form.

Einige lineare Gleichungen in zwei Variablen können auf die kanonische Form reduziert werden.

Zum Beispiel die Gleichung 2(16X+ 3y- 4) = 2(12 + 8X − j) kann in Erinnerung gerufen werden Axt + by = c. Öffnen wir die Klammern in beiden Teilen dieser Gleichung, erhalten wir 32X + 6j − 8 = 24 + 16X − 2j . Die Terme, die Unbekannte enthalten, werden auf der linken Seite der Gleichung gruppiert, und die Terme, die keine Unbekannten enthalten, werden auf der rechten Seite gruppiert. Dann bekommen wir 32X - 16X+ 6j+ 2j = 24 + 8 . Bringen wir in beiden Teilen ähnliche Terme ein, erhalten wir Gleichung 16 X+ 8j= 32. Diese Gleichung wird auf die Form reduziert Axt + by = c und ist kanonisch.

Gleichung 25 wurde zuvor betrachtet X+ 10j= 200 ist ebenfalls eine lineare Gleichung mit zwei Variablen in kanonischer Form. In dieser Gleichung sind die Parameter A , B Und C entsprechen den Werten 25, 10 bzw. 200.

Eigentlich die Gleichung Axt + by = c hat unendlich viele Lösungen. Lösen der Gleichung 25X+ 10j= 200, Wir haben nach seinen Wurzeln nur auf der Menge der ganzen Zahlen gesucht. Als Ergebnis erhielten wir mehrere Wertepaare, die diese Gleichung in eine Identität verwandelten. Aber auf der Menge der rationalen Zahlen Gleichung 25 X+ 10j= 200 wird unendlich viele Lösungen haben.

Um neue Wertepaare zu erhalten, müssen Sie einen beliebigen Wert für annehmen X, dann ausdrücken j. Nehmen wir zum Beispiel eine Variable X Wert 7. Dann erhalten wir eine Gleichung mit einer Variablen 25×7 + 10j= 200 in dem man sich ausdrücken kann j

Lassen X= 15 . Dann die Gleichung 25X+ 10j= 200 wird zu 25 × 15 + 10j= 200. Von hier aus finden wir das j = −17,5

Lassen X= −3 . Dann die Gleichung 25X+ 10j= 200 wird zu 25 × (−3) + 10j= 200. Von hier aus finden wir das j = −27,5

System aus zwei linearen Gleichungen mit zwei Variablen

Für die Gleichung Axt + by = c Sie können beliebig oft beliebige Werte dafür annehmen X und finde Werte für j. Für sich genommen wird eine solche Gleichung unendlich viele Lösungen haben.

Es kommt aber auch vor, dass die Variablen X Und j nicht durch eine, sondern durch zwei Gleichungen verbunden. In diesem Fall bilden sie die sogenannten System linearer Gleichungen mit zwei Variablen. Ein solches Gleichungssystem kann ein Wertepaar (oder anders gesagt: „eine Lösung“) haben.

Es kann auch vorkommen, dass das System überhaupt keine Lösungen hat. Ein lineares Gleichungssystem kann in seltenen Ausnahmefällen unendlich viele Lösungen haben.

Zwei lineare Gleichungen bilden ein System, wenn die Werte X Und j sind in jeder dieser Gleichungen enthalten.

Kehren wir zur allerersten Gleichung 25 zurück X+ 10j= 200 . Eines der Wertepaare für diese Gleichung war das Paar (6; 5). Dies ist der Fall, wenn man für 200 Rubel 6 Kuchen und 5 Tassen Kaffee kaufen könnte.

Stellen wir das Problem so zusammen, dass das Paar (6; 5) wird die einzige Lösung für Gleichung 25 X+ 10j= 200 . Dazu stellen wir eine weitere Gleichung auf, die dasselbe verbinden würde X Kuchen und j Tassen Kaffee.

Lassen Sie uns den Text der Aufgabe wie folgt formulieren:

„Ein Schüler kaufte mehrere Kuchen und mehrere Tassen Kaffee für 200 Rubel. Ein Kuchen kostet 25 Rubel und eine Tasse Kaffee kostet 10 Rubel. Wie viele Kuchen und Tassen Kaffee hat der Schüler gekauft, wenn bekannt ist, dass die Anzahl der Kuchen um eins größer ist als die Anzahl der Tassen Kaffee?

Wir haben bereits die erste Gleichung. Dies ist Gleichung 25 X+ 10j= 200 . Schreiben wir nun eine Gleichung für die Bedingung „Die Anzahl der Kuchen ist eine Einheit mehr als die Anzahl der Tassen Kaffee“ .

Die Anzahl der Kuchen beträgt X, und die Anzahl der Tassen Kaffee ist j. Sie können diesen Satz mithilfe der Gleichung schreiben x − y= 1. Diese Gleichung würde bedeuten, dass der Unterschied zwischen Kuchen und Kaffee 1 beträgt.

x=y+ 1 . Diese Gleichung bedeutet, dass die Anzahl der Kuchen um eins größer ist als die Anzahl der Tassen Kaffee. Um Gleichheit zu erreichen, wird daher eins zur Anzahl der Tassen Kaffee addiert. Dies kann leicht verstanden werden, wenn wir das Gewichtsmodell verwenden, das wir bei der Untersuchung der einfachsten Probleme berücksichtigt haben:

Habe zwei Gleichungen: 25 X+ 10j= 200 und x=y+ 1. Da die Werte X Und j, nämlich 6 und 5 sind in jeder dieser Gleichungen enthalten, dann bilden sie zusammen ein System. Schreiben wir dieses System auf. Bilden die Gleichungen ein System, so werden sie durch das Vorzeichen des Systems eingerahmt. Das Systemzeichen ist eine geschweifte Klammer:

Lassen Sie uns dieses System lösen. Dadurch können wir sehen, wie wir zu den Werten 6 und 5 kommen. Es gibt viele Methoden zur Lösung solcher Systeme. Betrachten Sie die beliebtesten davon.

Substitutionsmethode

Der Name dieser Methode spricht für sich. Sein Wesen besteht darin, eine Gleichung durch eine andere zu ersetzen, nachdem zuvor eine der Variablen ausgedrückt wurde.

In unserem System muss nichts ausgedrückt werden. In der zweiten Gleichung X = j+ 1 Variable X schon geäußert. Diese Variable entspricht dem Ausdruck j+ 1 . Dann können Sie diesen Ausdruck anstelle der Variablen in die erste Gleichung einsetzen X

Nach dem Ersetzen des Ausdrucks j+ 1 stattdessen in die erste Gleichung ein X, wir erhalten die Gleichung 25(j+ 1) + 10j= 200 . Dies ist eine lineare Gleichung mit einer Variablen. Diese Gleichung ist ganz einfach zu lösen:

Wir haben den Wert der Variablen gefunden j. Jetzt setzen wir diesen Wert in eine der Gleichungen ein und ermitteln den Wert X. Hierzu ist es zweckmäßig, die zweite Gleichung zu verwenden X = j+ 1 . Lassen Sie uns Wert darauf legen j

Das Paar (6; 5) ist also eine Lösung des Gleichungssystems, wie wir es beabsichtigt haben. Wir prüfen und stellen sicher, dass das Paar (6; 5) das System erfüllt:

Beispiel 2

Ersetzen Sie die erste Gleichung X= 2 + j in die zweite Gleichung 3 X - 2j= 9 . In der ersten Gleichung die Variable X ist gleich dem Ausdruck 2 + j. Wir setzen diesen Ausdruck stattdessen in die zweite Gleichung ein X

Lassen Sie uns nun den Wert ermitteln X. Ersetzen Sie dazu den Wert j in die erste Gleichung ein X= 2 + j

Die Lösung des Systems ist also der Paarwert (5; 3)

Beispiel 3. Lösen Sie das folgende Gleichungssystem mit der Substitutionsmethode:

Im Gegensatz zu den vorherigen Beispielen wird hier eine der Variablen nicht explizit ausgedrückt.

Um eine Gleichung durch eine andere zu ersetzen, benötigen Sie zunächst .

Es ist wünschenswert, die Variable auszudrücken, die einen Koeffizienten von eins hat. Die Koeffizienteneinheit hat eine Variable X, die in der ersten Gleichung enthalten ist X+ 2j= 11 . Lassen Sie uns diese Variable ausdrücken.

Nach einem variablen Ausdruck X, unser System wird so aussehen:

Jetzt setzen wir die erste Gleichung in die zweite ein und ermitteln den Wert j

Ersatz j X

Die Lösung des Systems ist also ein Wertepaar (3; 4)

Natürlich können Sie auch eine Variable ausdrücken j. Die Wurzeln werden sich nicht ändern. Aber wenn Sie es ausdrücken ja, Das Ergebnis ist keine sehr einfache Gleichung, deren Lösung mehr Zeit in Anspruch nehmen wird. Es wird so aussehen:

Wir sehen das darin dieses Beispiel ausdrücken X viel bequemer als auszudrücken j .

Beispiel 4. Lösen Sie das folgende Gleichungssystem mit der Substitutionsmethode:

Drücken Sie in der ersten Gleichung aus X. Dann nimmt das System die Form an:

j

Ersatz j in die erste Gleichung einsetzen und finden X. Sie können die ursprüngliche Gleichung 7 verwenden X+ 9j= 8 oder verwenden Sie die Gleichung, in der die Variable ausgedrückt wird X. Wir werden diese Gleichung verwenden, weil sie praktisch ist:

Die Lösung des Systems ist also das Wertepaar (5; −3)

Additionsmethode

Bei der Additionsmethode werden die im System enthaltenen Gleichungen Term für Term addiert. Diese Addition führt zu einer neuen Gleichung mit einer Variablen. Und es ist ziemlich einfach, diese Gleichung zu lösen.

Lösen wir das folgende Gleichungssystem:

Addiere die linke Seite der ersten Gleichung zur linken Seite der zweiten Gleichung. Und die rechte Seite der ersten Gleichung mit der rechten Seite der zweiten Gleichung. Wir erhalten die folgende Gleichheit:

Hier sind ähnliche Begriffe:

Als Ergebnis haben wir die einfachste Gleichung 3 erhalten X= 27, deren Wurzel 9 ist. Den Wert kennen X Sie können den Wert finden j. Ersetzen Sie den Wert X in die zweite Gleichung x − y= 3 . Wir erhalten 9 − j= 3 . Von hier j= 6 .

Die Lösung des Systems ist also ein Wertepaar (9; 6)

Beispiel 2

Addiere die linke Seite der ersten Gleichung zur linken Seite der zweiten Gleichung. Und die rechte Seite der ersten Gleichung mit der rechten Seite der zweiten Gleichung. In der resultierenden Gleichheit präsentieren wir ähnliche Begriffe:

Als Ergebnis erhielten wir die einfachste Gleichung 5 X= 20, dessen Wurzel 4 ist. Den Wert kennen X Sie können den Wert finden j. Ersetzen Sie den Wert X in die erste Gleichung 2 x+y= 11 . Lass uns 8+ bekommen j= 11 . Von hier j= 3 .

Die Lösung des Systems ist also das Wertepaar (4;3)

Der Additionsprozess wird nicht im Detail beschrieben. Es muss im Kopf geschehen. Beim Addieren müssen beide Gleichungen auf die kanonische Form zurückgeführt werden. Das heißt, für den Geist ac+by=c .

Aus den betrachteten Beispielen ist ersichtlich, dass das Hauptziel des Hinzufügens von Gleichungen darin besteht, eine der Variablen zu entfernen. Allerdings ist es nicht immer möglich, das Gleichungssystem sofort mit der Additionsmethode zu lösen. Meistens wird das System vorab in eine Form gebracht, in der es möglich ist, die in diesem System enthaltenen Gleichungen hinzuzufügen.

Zum Beispiel das System kann direkt durch die Additionsmethode gelöst werden. Bei der Addition beider Gleichungen ergeben sich die Terme j Und −y verschwinden, weil ihre Summe Null ist. Als Ergebnis wird die einfachste Gleichung gebildet 11 X= 22 , dessen Wurzel 2 ist. Dann wird es möglich sein, zu bestimmen j gleich 5.

Und das Gleichungssystem Die Additionsmethode kann nicht sofort gelöst werden, da dies nicht zum Verschwinden einer der Variablen führt. Die Addition führt zu Gleichung 8 X+ j= 28 , das unendlich viele Lösungen hat.

Wenn beide Teile der Gleichung mit derselben Zahl ungleich Null multipliziert oder dividiert werden, erhält man eine der angegebenen Gleichung äquivalente Gleichung. Diese Regel gilt auch für ein lineares Gleichungssystem mit zwei Variablen. Eine der Gleichungen (oder beide Gleichungen) kann mit einer Zahl multipliziert werden. Das Ergebnis ist ein äquivalentes System, dessen Wurzeln mit dem vorherigen übereinstimmen.

Kehren wir zum allerersten System zurück, in dem beschrieben wurde, wie viele Kuchen und Tassen Kaffee der Schüler gekauft hat. Die Lösung dieses Systems war ein Wertepaar (6; 5).

Wir multiplizieren beide in diesem System enthaltenen Gleichungen mit einigen Zahlen. Nehmen wir an, wir multiplizieren die erste Gleichung mit 2 und die zweite mit 3

Das Ergebnis ist ein System
Die Lösung dieses Systems ist immer noch das Wertepaar (6; 5)

Dies bedeutet, dass die im System enthaltenen Gleichungen auf eine für die Anwendung der Additionsmethode geeignete Form reduziert werden können.

Zurück zum System , was wir mit der Additionsmethode nicht lösen konnten.

Multiplizieren Sie die erste Gleichung mit 6 und die zweite mit −2

Dann erhalten wir das folgende System:

Wir fügen die in diesem System enthaltenen Gleichungen hinzu. Hinzufügen von Komponenten 12 X und -12 X ergibt 0, Addition 18 j und 4 j wird 22 geben j, und die Addition von 108 und −20 ergibt 88. Dann erhält man die Gleichung 22 j= 88, daher j = 4 .

Wenn es Ihnen zunächst schwerfällt, Gleichungen im Kopf hinzuzufügen, können Sie aufschreiben, wie die linke Seite der ersten Gleichung zur linken Seite der zweiten Gleichung und die rechte Seite der ersten Gleichung zur rechten Seite der hinzugefügt wird zweite Gleichung:

Wissen, dass der Wert der Variablen j 4 ist, können Sie den Wert finden X. Ersatz j in eine der Gleichungen, zum Beispiel in die erste Gleichung 2 X+ 3j= 18 . Dann erhalten wir eine Gleichung mit einer Variablen 2 X+ 12 = 18 . Wir übertragen 12 auf die rechte Seite, ändern das Vorzeichen und erhalten 2 X= 6, also X = 3 .

Beispiel 4. Lösen Sie das folgende Gleichungssystem mit der Additionsmethode:

Multiplizieren Sie die zweite Gleichung mit −1. Dann nimmt das System die folgende Form an:

Addieren wir beide Gleichungen. Hinzufügen von Komponenten X Und −x ergibt 0, Addition 5 j und 3 j gebe 8 j und die Addition von 7 und 1 ergibt 8. Das Ergebnis ist Gleichung 8 j= 8, dessen Wurzel 1 ist. Wissen, dass der Wert j 1 ist, können Sie den Wert finden X .

Ersatz j in die erste Gleichung erhalten wir X+ 5 = 7 also X= 2

Beispiel 5. Lösen Sie das folgende Gleichungssystem mit der Additionsmethode:

Es ist wünschenswert, dass die Begriffe, die dieselben Variablen enthalten, untereinander stehen. Daher sind in der zweiten Gleichung die Terme 5 j und −2 X Plätze tauschen. Als Ergebnis wird das System die Form annehmen:

Multiplizieren Sie die zweite Gleichung mit 3. Dann nimmt das System die Form an:

Nun addieren wir beide Gleichungen. Als Ergebnis der Addition erhalten wir Gleichung 8 j= 16 , dessen Wurzel 2 ist.

Ersatz j In die erste Gleichung erhalten wir 6 X− 14 = 40 . Wir übertragen den Term −14 auf die rechte Seite, ändern das Vorzeichen und erhalten 6 X= 54 . Von hier X= 9.

Beispiel 6. Lösen Sie das folgende Gleichungssystem mit der Additionsmethode:

Lassen Sie uns Brüche loswerden. Multiplizieren Sie die erste Gleichung mit 36 ​​und die zweite mit 12

Im resultierenden System Die erste Gleichung kann mit −5 und die zweite mit 8 multipliziert werden

Fügen wir die Gleichungen zum resultierenden System hinzu. Dann erhalten wir die einfachste Gleichung −13 j= −156 . Von hier j= 12 . Ersatz j in die erste Gleichung einsetzen und finden X

Beispiel 7. Lösen Sie das folgende Gleichungssystem mit der Additionsmethode:

Wir bringen beide Gleichungen in die Normalform. Hier bietet es sich an, die Proportionsregel in beiden Gleichungen anzuwenden. Wenn in der ersten Gleichung die rechte Seite als dargestellt wird und die rechte Seite der zweiten Gleichung als , dann nimmt das System die Form an:

Wir haben einen Anteil. Wir multiplizieren seine Extrem- und Mittelterme. Dann nimmt das System die Form an:

Wir multiplizieren die erste Gleichung mit −3 und öffnen die Klammern in der zweiten:

Nun addieren wir beide Gleichungen. Als Ergebnis der Addition dieser Gleichungen erhalten wir eine Gleichheit, in deren beiden Teilen Null steht:

Es stellt sich heraus, dass das System unendlich viele Lösungen hat.

Aber wir können nicht einfach beliebige Werte vom Himmel nehmen X Und j. Wir können einen der Werte angeben, der andere wird abhängig von dem von uns angegebenen Wert bestimmt. Lassen Sie zum Beispiel X= 2 . Ersetzen Sie diesen Wert im System:

Als Ergebnis der Lösung einer der Gleichungen wird der Wert für j, was beide Gleichungen erfüllt:

Das resultierende Wertepaar (2; −2) erfüllt das System:

Suchen wir ein weiteres Wertepaar. Lassen X= 4. Setzen Sie diesen Wert in das System ein:

Das kann man mit dem Auge feststellen j gleich Null. Dann erhalten wir ein Wertepaar (4; 0), das unserem System genügt:

Beispiel 8. Lösen Sie das folgende Gleichungssystem mit der Additionsmethode:

Multiplizieren Sie die erste Gleichung mit 6 und die zweite mit 12

Schreiben wir um, was noch übrig ist:

Multiplizieren Sie die erste Gleichung mit −1. Dann nimmt das System die Form an:

Nun addieren wir beide Gleichungen. Als Ergebnis der Addition wird Gleichung 6 gebildet B= 48 , dessen Wurzel 8 ist. Ersatz B in die erste Gleichung einsetzen und finden A

System linearer Gleichungen mit drei Variablen

Eine lineare Gleichung mit drei Variablen enthält drei Variablen mit Koeffizienten sowie einen Achsenabschnitt. In kanonischer Form kann es wie folgt geschrieben werden:

ax + by + cz = d

Diese Gleichung hat unendlich viele Lösungen. Geben Sie zwei Variablen an verschiedene Bedeutungen, können Sie den dritten Wert finden. Die Lösung ist in diesem Fall das Wertetripel ( X; y; z), was die Gleichung in eine Identität umwandelt.

Wenn Variablen x, y, z durch drei Gleichungen miteinander verbunden sind, dann entsteht ein System aus drei linearen Gleichungen mit drei Variablen. Um ein solches System zu lösen, können Sie dieselben Methoden anwenden, die auch für lineare Gleichungen mit zwei Variablen gelten: die Substitutionsmethode und die Additionsmethode.

Beispiel 1. Lösen Sie das folgende Gleichungssystem mit der Substitutionsmethode:

Wir drücken in der dritten Gleichung aus X. Dann nimmt das System die Form an:

Jetzt machen wir die Substitution. Variable X ist gleich dem Ausdruck 3 − 2j − 2z . Setzen Sie diesen Ausdruck in die erste und zweite Gleichung ein:

Öffnen wir die Klammern in beiden Gleichungen und geben ähnliche Terme an:

Wir sind zu einem System linearer Gleichungen mit zwei Variablen gekommen. In diesem Fall ist es zweckmäßig, die Additionsmethode anzuwenden. Als Ergebnis die Variable j verschwindet und wir können den Wert der Variablen finden z

Lassen Sie uns nun den Wert ermitteln j. Hierzu ist es zweckmäßig, die Gleichung − zu verwenden j+ z= 4. Ersetzen Sie den Wert z

Lassen Sie uns nun den Wert ermitteln X. Hierzu ist es zweckmäßig, die Gleichung zu verwenden X= 3 − 2j − 2z . Ersetzen Sie die Werte darin j Und z

Somit ist das Wertetripel (3; −2; 2) die Lösung unseres Systems. Durch die Prüfung stellen wir sicher, dass diese Werte dem System genügen:

Beispiel 2. Lösen Sie das System mit der Additionsmethode

Addieren wir die erste Gleichung mit der zweiten multipliziert mit −2.

Wenn die zweite Gleichung mit −2 multipliziert wird, nimmt sie die Form an −6X+ 6y- 4z = −4 . Fügen Sie es nun zur ersten Gleichung hinzu:

Wir sehen, dass als Ergebnis elementarer Transformationen der Wert der Variablen bestimmt wurde X. Es ist gleich eins.

Zurück zu Hauptsystem. Addieren wir die zweite Gleichung mit der dritten multipliziert mit −1. Wenn die dritte Gleichung mit −1 multipliziert wird, nimmt sie die Form an −4X + 5j − 2z = −1 . Fügen Sie es nun zur zweiten Gleichung hinzu:

Habe die Gleichung verstanden X - 2j= −1 . Setzen Sie den Wert darin ein X was wir früher gefunden haben. Dann können wir den Wert ermitteln j

Wir kennen jetzt die Werte X Und j. Dadurch können Sie den Wert ermitteln z. Wir verwenden eine der im System enthaltenen Gleichungen:

Somit ist das Wertetripel (1; 1; 1) die Lösung unseres Systems. Durch die Prüfung stellen wir sicher, dass diese Werte dem System genügen:

Aufgaben zur Erstellung linearer Gleichungssysteme

Die Aufgabe, Gleichungssysteme aufzustellen, wird durch die Einführung mehrerer Variablen gelöst. Als nächstes werden Gleichungen basierend auf den Bedingungen des Problems zusammengestellt. Aus den aufgestellten Gleichungen bilden sie ein System und lösen es. Nachdem das System gelöst wurde, muss überprüft werden, ob seine Lösung die Bedingungen des Problems erfüllt.

Aufgabe 1. Ein Wolga-Wagen verließ die Stadt in Richtung Kolchose. Sie kehrte auf einer anderen Straße zurück, die 5 km kürzer war als die erste. Insgesamt legte das Auto 35 km in beide Richtungen zurück. Wie viele Kilometer ist jede Straße lang?

Lösung

Lassen X- Länge der ersten Straße, j- die Länge der Sekunde. Wenn das Auto 35 km in beide Richtungen zurückgelegt hat, kann die erste Gleichung wie folgt geschrieben werden: X+ j= 35. Diese Gleichung beschreibt die Summe der Längen beider Straßen.

Es wird gesagt, dass das Auto auf der Straße zurückfuhr, die um 5 km kürzer war als die erste. Dann kann die zweite Gleichung geschrieben werden als X− j= 5. Diese Gleichung zeigt, dass der Unterschied zwischen den Straßenlängen 5 km beträgt.

Oder die zweite Gleichung kann geschrieben werden als X= j+ 5 . Wir werden diese Gleichung verwenden.

Da die Variablen X Und j in beiden Gleichungen die gleiche Zahl bezeichnen, dann können wir daraus ein System bilden:

Lassen Sie uns dieses System mit einer der zuvor untersuchten Methoden lösen. In diesem Fall ist es zweckmäßig, die Substitutionsmethode zu verwenden, da in der zweiten Gleichung die Variable X schon geäußert.

Setze die zweite Gleichung in die erste ein und finde j

Ersetzen Sie den gefundenen Wert j in die zweite Gleichung X= j+ 5 und finden X

Die Länge der ersten Straße wurde durch die Variable angegeben X. Jetzt haben wir seine Bedeutung gefunden. Variable X ist 20. Die Länge der ersten Straße beträgt also 20 km.

Und die Länge der zweiten Straße wurde durch angegeben j. Der Wert dieser Variablen beträgt 15. Die Länge der zweiten Straße beträgt also 15 km.

Machen wir einen Check. Stellen wir zunächst sicher, dass das System richtig gelöst ist:

Prüfen wir nun, ob die Lösung (20; 15) die Bedingungen des Problems erfüllt.

Insgesamt soll das Auto 35 km in beide Richtungen gefahren sein. Wir addieren die Längen beider Straßen und stellen sicher, dass die Lösung (20; 15) erfüllt dieser Zustand: 20 km + 15 km = 35 km

Nächste Bedingung: Das Auto fuhr auf einer anderen Straße zurück, die 5 km kürzer war als die erste . Wir sehen, dass die Lösung (20; 15) auch diese Bedingung erfüllt, da 15 km um 5 km kürzer als 20 km sind: 20 km − 15 km = 5 km

Bei der Zusammenstellung eines Systems ist es wichtig, dass die Variablen in allen in diesem System enthaltenen Gleichungen die gleichen Zahlen bezeichnen.

Unser System enthält also zwei Gleichungen. Diese Gleichungen enthalten wiederum die Variablen X Und j, die in beiden Gleichungen die gleichen Zahlen bezeichnen, nämlich die Straßenlängen von 20 km und 15 km.

Aufgabe 2. Auf den Bahnsteig wurden Eichen- und Kiefernschwellen geladen, insgesamt 300 Schwellen. Es ist bekannt, dass alle Eichenschwellen 1 Tonne weniger wogen als alle Kiefernschwellen. Bestimmen Sie, wie viele Eichen- und Kiefernschwellen es getrennt gab, wenn jede Eichenschwelle 46 kg und jede Kiefernschwelle 28 kg wog.

Lösung

Lassen X Eiche und j Kiefernschwellen wurden auf den Bahnsteig geladen. Wenn es insgesamt 300 Schwellen gäbe, kann die erste Gleichung wie folgt geschrieben werden: x+y = 300 .

Alle Eichenschwellen wogen 46 X kg und Kiefer wogen 28 j kg. Da Eichenschwellen 1 Tonne weniger wogen als Kiefernschwellen, kann die zweite Gleichung wie folgt geschrieben werden: 28y- 46X= 1000 . Diese Gleichung zeigt, dass der Massenunterschied zwischen Eichen- und Kiefernschwellen 1000 kg beträgt.

Tonnen wurden in Kilogramm umgerechnet, da die Masse von Eichen- und Kiefernschwellen in Kilogramm gemessen wird.

Als Ergebnis erhalten wir zwei Gleichungen, die das System bilden

Lassen Sie uns dieses System lösen. Drücken Sie in der ersten Gleichung aus X. Dann nimmt das System die Form an:

Setze die erste Gleichung in die zweite ein und finde j

Ersatz j in die Gleichung ein X= 300 − j und finden Sie heraus, was X

Das bedeutet, dass 100 Eichen- und 200 Kiefernholzschwellen auf den Bahnsteig geladen wurden.

Überprüfen wir, ob die Lösung (100; 200) die Bedingungen des Problems erfüllt. Stellen wir zunächst sicher, dass das System richtig gelöst ist:

Es hieß, es seien insgesamt 300 Schläfer gewesen. Wir addieren die Anzahl der Eichen- und Kiefernschwellen und stellen sicher, dass die Lösung (100; 200) diese Bedingung erfüllt: 100 + 200 = 300.

Nächste Bedingung: Alle Eichenschwellen wogen 1 Tonne weniger als alle Kiefernholzschwellen . Wir sehen, dass die Lösung (100; 200) auch diese Bedingung erfüllt, da 46 × 100 kg Eichenschwellen leichter sind als 28 × 200 kg Kiefernschwellen: 5600 kg − 4600 kg = 1000 kg.

Aufgabe 3. Wir haben drei Stücke einer Legierung aus Kupfer und Nickel im Gewichtsverhältnis 2:1, 3:1 und 5:1 genommen. Davon wurde ein 12 kg schweres Stück mit einem Verhältnis von Kupfer- und Nickelgehalt von 4:1 verschmolzen. Ermitteln Sie die Masse jedes Originalstücks, wenn die Masse des ersten Stücks doppelt so groß ist wie die Masse des zweiten.