heim › Motor › Konstruktion von Polyederabschnitten. Forschungsarbeit zum Thema „Methoden zur Konstruktion von Polyederabschnitten“

Konstruktion von Polyederabschnitten. Forschungsarbeit zum Thema „Methoden zur Konstruktion von Polyederabschnitten“

Die Aufgabe selbst läuft normalerweise so ab: „Bauen Sie eine natürliche Ansicht der Schnittfigur auf“. Natürlich haben wir beschlossen, diese Frage nicht außer Acht zu lassen und versuchen, wenn möglich, zu erklären, wie der Schrägschnitt aufgebaut ist.

Um zu erklären, wie ein Schrägschnitt aufgebaut ist, gebe ich einige Beispiele. Natürlich werde ich mit dem Elementaren beginnen und die Komplexität der Beispiele schrittweise steigern. Ich hoffe, dass Sie nach der Analyse dieser Beispiele von Schnittzeichnungen verstehen, wie dies geschieht, und Ihre Lernaufgabe selbst lösen können.

Betrachten Sie einen „Ziegelstein“ mit den Maßen 40x60x80 mm durch eine beliebige schiefe Ebene. Die Schnittebene schneidet es entlang der Punkte 1-2-3-4. Ich denke, hier ist alles klar.

Fahren wir mit der Konstruktion einer natürlichen Form der Schnittfigur fort.
1. Zeichnen wir zunächst die Achse des Abschnitts. Die Achse sollte parallel zur Schnittebene gezeichnet werden – parallel zur Linie, in die die Ebene in der Hauptansicht projiziert wird – normalerweise ist die Hauptansicht die Aufgabe, für die sie gestellt wird Konstruktion eines schrägen Abschnitts(Im Folgenden werde ich immer die Hauptansicht erwähnen, da dies bei Trainingszeichnungen fast immer der Fall ist).
2. Auf der Achse legen wir die Länge des Abschnitts beiseite. In meiner Zeichnung wird es mit L bezeichnet. Die Größe L wird in der Hauptansicht bestimmt und entspricht dem Abstand vom Punkt, an dem der Abschnitt in das Teil eintritt, bis zum Punkt, an dem er austritt.
3. Von den resultierenden zwei Punkten auf der Achse senkrecht dazu legen wir die Abschnittsbreiten an diesen Punkten beiseite. In der Draufsicht kann die Breite des Abschnitts am Eintrittspunkt in das Bauteil und am Austrittspunkt aus dem Bauteil ermittelt werden. IN dieser Fall beide Segmente 1-4 und 2-3 sind gleich 60 mm. Wie Sie auf dem Bild oben sehen können, sind die Kanten des Abschnitts gerade, also verbinden wir einfach unsere beiden resultierenden Segmente und erhalten ein Rechteck 1-2-3-4. Dies ist die natürliche Form des Abschnitts unseres Ziegels mit einer schiefen Ebene.

Lassen Sie uns nun unser Detail verkomplizieren. Legen wir einen Ziegelstein 120x80x20 mm auf die Basis und fügen der Figur Versteifungen hinzu. Zeichnen wir eine Schnittebene so, dass sie durch alle vier Elemente der Figur verläuft (durch die Basis, den Ziegelstein und zwei Versteifungen). Im Bild unten sehen Sie drei Ansichten und ein realistisches Bild dieses Teils.

Versuchen wir, eine natürliche Ansicht dieses schrägen Abschnitts zu erstellen. Beginnen wir noch einmal mit der Schnittachse: Zeichnen Sie sie parallel zur Schnittebene, die in der Hauptansicht angezeigt wird. Darauf legen wir die Länge des Abschnitts fest gleich A-E. Punkt A ist der Eintrittspunkt des Abschnitts in das Teil und in einem bestimmten Fall der Eintrittspunkt des Abschnitts in die Basis. Der Austrittspunkt aus der Basis ist Punkt B. Markieren wir Punkt B auf der Achse des Abschnitts. Ebenso markieren wir die Ein- und Ausstiegspunkte zur Kante, zum „Ziegel“ und zur zweiten Kante. Von den Punkten A und B senkrecht zur Achse legen wir Segmente beiseite, die der Breite der Basis entsprechen (auf jeder Seite der Achse 40, nur 80 mm). Verbinden Extrempunkte- Wir erhalten ein Rechteck, das eine natürliche Ansicht des Abschnitts der Basis des Teils darstellt.

Jetzt ist es an der Zeit, einen Abschnitt zu erstellen, bei dem es sich um einen Abschnitt der Kante des Teils handelt. Von den Punkten B und C legen wir Senkrechte von 5 mm in jede Richtung beiseite – wir erhalten Segmente von 10 mm. Verbinden Sie die Extrempunkte und erhalten Sie den Querschnitt der Rippe.

Von den Punkten C und D legen wir senkrechte Segmente beiseite, die der Breite des „Ziegelsteins“ entsprechen – ganz ähnlich dem ersten Beispiel dieser Lektion.

Nachdem wir die Senkrechten von den Punkten D und E entsprechend der Breite der zweiten Kante beiseite gelegt und die Extrempunkte verbunden haben, erhalten wir eine natürliche Ansicht ihres Schnitts.

Es bleibt übrig, die Brücken zwischen den einzelnen Elementen des resultierenden Abschnitts zu löschen und eine Schraffur anzuwenden. Sie sollten so etwas erhalten:

Wenn wir die Zahl gemäß einem bestimmten Abschnitt teilen, erhalten wir die folgende Ansicht:

Ich hoffe, Sie lassen sich von den langwierigen Absätzen der Beschreibung des Algorithmus nicht einschüchtern. Wenn Sie alles oben Gesagte gelesen haben und es immer noch nicht vollständig verstehen, wie man einen Querschnitt zeichnet Ich rate Ihnen dringend, ein Blatt Papier und einen Bleistift in die Hand zu nehmen und zu versuchen, alle Schritte nach mir zu wiederholen – das wird Ihnen beim Erlernen des Stoffes fast zu 100 % helfen.

Einmal habe ich die Fortsetzung dieses Artikels versprochen. Abschließend bin ich bereit, Ihnen eine schrittweise Konstruktion eines schrägen Abschnitts eines Teils vorzustellen, die näher am Niveau einer Hausaufgabe liegt. Darüber hinaus wird der schräge Abschnitt in der dritten Ansicht definiert (der schräge Abschnitt wird in der linken Ansicht definiert).

oder Notieren Sie sich unsere Telefonnummer und erzählen Sie Ihren Freunden von uns – wahrscheinlich sucht jemand nach einer Möglichkeit, Zeichnungen anzufertigen

oder Erstellen Sie eine Notiz zu unseren Lektionen auf Ihrer Seite oder Ihrem Blog – und jemand anderes wird in der Lage sein, die Zeichnung zu beherrschen.

Ja, alles ist in Ordnung, aber ich würde gerne sehen, wie das Gleiche an einem komplexeren Teil gemacht wird, zum Beispiel mit Fasen und einem kegelförmigen Loch.

Danke. Aber sind die Versteifungen auf den Einschnitten nicht schraffiert?
Exakt. Sie sind es, die nicht schlüpfen. Weil sie sind Allgemeine Regeln Schnitte machen. Sie werden jedoch normalerweise schraffiert, wenn Schnitte in axonometrischen Projektionen vorgenommen werden – Isometrie, Dimetrie usw. Bei geneigten Abschnitten wird auch der zur Steife gehörige Bereich schattiert.

Vielen Dank, sehr zugänglich. Können Sie mir sagen, ob der schräge Abschnitt in der Draufsicht oder in der linken Ansicht ausgeführt werden kann? Wenn ja, würde ich gerne das einfachste Beispiel sehen. Bitte.

Solche Schnitte sind möglich. Aber leider habe ich gerade kein Beispiel zur Hand. Und da ist noch einer interessanter Punkt: Einerseits gibt es da nichts Neues, andererseits ist es in der Praxis wirklich schwieriger, solche Abschnitte zu zeichnen. Aus irgendeinem Grund beginnt im Kopf alles durcheinander zu geraten und die meisten Schüler haben Schwierigkeiten. Aber gib nicht auf!

Ja, alles ist in Ordnung, aber ich würde gerne sehen, wie das Gleiche gemacht wird, aber mit Löchern (durchgehend und nicht durchgehend), sonst verwandeln sie sich in meinem Kopf nie in eine Ellipse

Helfen Sie mir bei einem komplexen Problem

Schade, dass du hier geschrieben hast. Wir würden in der Post schreiben – vielleicht hätten wir Zeit, alles zu besprechen.

Du erklärst es gut. Was ist, wenn eine Seite des Teils halbkreisförmig ist? Außerdem weist das Teil Löcher auf.

Ilya, nutzen Sie die Lektion aus dem Abschnitt über beschreibende Geometrie „Schnitt eines Zylinders durch eine schiefe Ebene“. Damit können Sie herausfinden, was mit Löchern (eigentlich sind es auch Zylinder) und einer halbkreisförmigen Seite zu tun ist.

Ich danke dem Autor für den Artikel! Kurz und verständlich. Vor etwa 20 Jahren habe ich selbst am Granit der Wissenschaft genagt, jetzt helfe ich meinem Sohn. Ich habe vieles vergessen, aber Ihr Artikel hat ein grundlegendes Verständnis des Themas vermittelt. Ich werde mich nun mit dem geneigten Abschnitt des Zylinders befassen)

Füge deinen Kommentar hinzu.

Axiome der Planimetrie:

In verschiedenen Lehrbüchern können die Eigenschaften von Linien und Ebenen auf unterschiedliche Weise dargestellt werden, in Form eines Axioms, einer Konsequenz daraus, eines Theorems, eines Lemmas usw. Betrachten Sie das Lehrbuch Pogorelov A.V.

Die Gerade teilt die Ebene in zwei Halbebenen.

Von jeder Halblinie zu einer gegebenen Halbebene kann man mit einem gegebenen Winkel abrechnen Gradmaß, weniger als 180 0 , und nur einer.

Was auch immer das Dreieck ist, es gibt an einem bestimmten Ort in Bezug auf die angegebene Halblinie ein gleichgroßes Dreieck.

Durch einen Punkt, der nicht auf einer gegebenen Geraden liegt, kann höchstens eine Gerade in der Ebene parallel zu der gegebenen Geraden gezogen werden.

Axiome der Stereometrie:

Was auch immer die Ebene ist, es gibt Punkte, die zu dieser Ebene gehören, und Punkte, die nicht zu dieser Ebene gehören, und Punkte, die nicht dazu gehören.

Wenn zwei verschiedene Ebenen einen gemeinsamen Punkt haben, dann schneiden sie sich entlang einer Geraden, die durch diesen Punkt verläuft.

Wenn zwei verschiedene Linien einen gemeinsamen Punkt haben, kann eine Ebene durch sie gezogen werden, und zwar nur eine.

Unabhängig von der Linie gibt es Punkte, die zu dieser Linie gehören, und Punkte, die nicht dazu gehören.

Durch zwei beliebige Punkte kann man eine Linie ziehen, und zwar nur einen.

Von den drei Punkten auf einer Linie liegt nur einer zwischen den beiden anderen.

Jedes Segment hat eine bestimmte Länge größer als Null. Die Länge eines Segments ist gleich der Summe der Längen der Teile, in die es durch einen seiner Punkte unterteilt wird.

Eine zu einer Ebene gehörende Gerade teilt diese Ebene in zwei Halbebenen.

Jeder Winkel hat ein bestimmtes Gradmaß größer als Null. Der gerade Winkel beträgt 180 0 . Das Gradmaß eines Winkels ist gleich der Summe der Gradmaße der Winkel, in die er durch einen zwischen seinen Seiten verlaufenden Strahl geteilt wird.

Auf jeder Halblinie von ihrem Startpunkt aus können Sie ein Segment einer bestimmten Länge verschieben, und zwar nur eines.

Von einer Halblinie auf der Ebene, die sie enthält, kann ein Winkel mit einem bestimmten Gradmaß kleiner als 180 in eine bestimmte Halbebene aufgetragen werden 0 , und nur einer.

Was auch immer das Dreieck ist, es gibt ein gleichgroßes Dreieck in der gegebenen Ebene an einer gegebenen Stelle relativ zur gegebenen Halblinie in dieser Ebene.

In einer Ebene kann durch einen gegebenen Punkt, der nicht auf einer gegebenen Geraden liegt, höchstens eine Gerade parallel zu der gegebenen Geraden gezogen werden.

Querschnitt

Im Raum können zwei Figuren, in unserem Fall eine Ebene und ein Polyeder, folgende gegenseitige Anordnung haben: sich nicht schneiden, sich in einem Punkt schneiden, sich in einer geraden Linie schneiden und die Ebene schneidet das Polyeder entlang seines Inneren (Abb. 1) , und bilden gleichzeitig die folgenden Figuren:

a) eine leere Figur (nicht schneiden)

b) Punkt

c) schneiden

d) Polygon

Wenn es am Schnittpunkt eines Polyeders und einer Ebene ein Polygon gibt, dann dieses Polygonheißt ein Abschnitt eines Polyeders mit einer Ebene .

Abb.1

Definition. Querschnitt Ein räumlicher Körper (z. B. ein Polyeder) ist eine Figur, die am Schnittpunkt eines Körpers mit einer Ebene entsteht.

Schnittebene Polyeder Nennen wir jede Ebene, auf deren beiden Seiten sich Punkte eines gegebenen Polyeders befinden.

Wir betrachten nur den Fall, dass die Ebene das Polyeder entlang seines Inneren schneidet. In diesem Fall ist der Schnittpunkt dieser Ebene mit jeder Fläche des Polyeders ein bestimmtes Segment.

Schneiden sich die Ebenen in einer Geraden, so heißt die Geradevon einem dieser Flugzeuge zum anderen.

Im allgemeinen Fall schneidet die Sekantenebene eines Polyeders die Ebene jeder seiner Flächen (sowie jede andere Sekantenebene dieses Polyeders). Es schneidet auch jede der Linien, auf denen die Kanten des Polyeders liegen.

Die Linie, entlang der die Sekantenebene die Ebene einer beliebigen Fläche des Polyeders schneidet, wird aufgerufender Schnittebene folgen auf der Ebene dieser Fläche, und der Punkt, an dem die Sekantenebene die Linie schneidet, die eine beliebige Kante des Polyeders enthält, wird aufgerufender Schnittebene folgen Andiese gerade Linie. Dieser Punkt ist auch die Spur einer Geraden auf der Schnittebene. Wenn die Schnittebene die Fläche des Polyeders direkt schneidet, können wir über die Spur der Schnittebene auf der Fläche und in ähnlicher Weise über sprechenSpur einer Schnittebene an einer Kante eines Polyeders, das heißt, die Spur einer Kante auf einer Schnittebene.

Da eine Gerade durch zwei Punkte eindeutig bestimmt ist, genügt es, zwei gemeinsame Punkte der Ebenen zu konstruieren, um die Spur einer Sekantenebene auf einer anderen Ebene und insbesondere auf der Ebene einer beliebigen Fläche eines Polyeders zu finden

Um eine Spur einer Sekantenebene zu konstruieren, sowie um einen Schnitt eines Polyeders durch diese Ebene zu konstruieren, muss nicht nur das Polyeder, sondern auch die Sekantenebene angegeben werden. Und die Konstruktion der Schnittebene erfolgt abhängig von der Zuordnung dieser Ebene. Die wichtigsten Möglichkeiten, eine Ebene und insbesondere eine Sekantenebene zu definieren, sind wie folgt:

drei Punkte, die nicht auf einer Geraden liegen;

eine gerade Linie und ein Punkt, der nicht darauf liegt;

zwei parallele Linien;

zwei sich schneidende Linien;

ein Punkt und zwei sich schneidende Linien;

Es gibt andere Möglichkeiten, die Schnittebene zu definieren.

Daher können alle Methoden zur Konstruktion von Polyederabschnitten in Methoden unterteilt werden.

Methoden zur Konstruktion von Polyederabschnitten

Die Methode der Polyederabschnitte in der Stereometrie wird bei Konstruktionsproblemen verwendet. Es basiert auf der Fähigkeit, einen Abschnitt eines Polyeders zu bilden und die Art des Abschnitts zu bestimmen.

Es gibt drei Hauptmethoden zum Konstruieren von Polyederabschnitten:

Axiomatische Methode:

Trace-Methode.

Kombinierte Methode.

Koordinatenmethode.

Notiz dass die Methode der Spuren und die Methode der Hilfsabschnitte Varianten sindAxiomatische Methode zur Konstruktion von Abschnitten.

Wir können auch die folgenden Methoden zur Konstruktion von Polyederabschnitten unterscheiden:

Konstruktion eines Abschnitts eines Polyeders durch eine Ebene, die durch einen gegebenen Punkt parallel zu einer gegebenen Ebene verläuft;

Konstruktion eines Abschnitts, der durch eine gegebene Linie parallel zu einer anderen gegebenen Linie verläuft;

Konstruktion eines Abschnitts, der durch einen gegebenen Punkt parallel zu zwei gegebenen Schräglinien verläuft;

Konstruktion eines Abschnitts eines Polyeders durch eine Ebene, die durch eine gegebene Linie senkrecht zu einer gegebenen Ebene verläuft;

Konstruktion eines Abschnitts eines Polyeders durch eine Ebene, die durch einen gegebenen Punkt senkrecht zu einer gegebenen Geraden verläuft.

Die Hauptaktionen, aus denen die Methoden zum Konstruieren von Schnitten bestehen, sind das Finden des Schnittpunkts einer geraden Linie mit einer Ebene, das Konstruieren einer Schnittlinie zweier Ebenen und das Konstruieren einer geraden Linie parallel zu einer Ebene senkrecht zur Ebene. Um eine gerade Schnittlinie zweier Ebenen zu konstruieren, werden normalerweise zwei ihrer Punkte gefunden und eine gerade Linie durch sie gezogen. Um den Schnittpunkt einer Linie und einer Ebene zu konstruieren, suchen Sie eine Linie in der Ebene, die die gegebene Linie schneidet. Dann erhält man den gewünschten Punkt am Schnittpunkt der gefundenen Geraden mit der gegebenen.

Betrachten Sie die von uns separat aufgeführten ArtikelMethoden zur Konstruktion von Polyederabschnitten:

Trace-Methode.

Trace-Methode basiert (operiert) auf den Axiomen der Stereometrie. Der Kern der Methode besteht darin, eine Hilfslinie zu konstruieren, die das Bild der Schnittlinie der Schnittebene mit der Ebene einer beliebigen Fläche der Figur ist. Am bequemsten ist es, ein Bild der Schnittlinie der Schnittebene mit der Ebene der unteren Basis zu erstellen. Diese Liniewird als Hauptspur der Schnittebene bezeichnet . Mithilfe der Spur lassen sich leicht Bilder der Punkte der Schnittebene konstruieren, die sich an den Seitenkanten oder Flächen der Figur befinden. Indem wir die Bilder dieser Punkte konsequent verbinden, erhalten wir das Bild des gewünschten Abschnitts.

Notiz dass bei der Konstruktion der Hauptspur der Sekantenebene die folgende Anweisung verwendet wird.

Wenn die Punkte zur Sekantenebene gehören und nicht auf einer Geraden liegen, und ihre Projektion (zentral oder parallel) auf die als Hauptebene gewählte Ebene sind dies jeweils die Punkte dann liegen die Schnittpunkte der entsprechenden Geraden, also die Punkte und, auf derselben Geraden (Abb. 1, a, b).

Abb.1.a Abb.1.b

Diese Linie ist die Hauptspur der Schnittebene. Da die Punkte auf der Hauptspur liegen, genügt es, zwei dieser drei Punkte zu finden, um sie zu konstruieren.

Methode der Hilfsabschnitte.

Diese Methode zur Konstruktion von Polyederabschnitten ist ausreichend universell. In Fällen, in denen die gewünschte(n) Spur(en) der Schnittebene außerhalb der Zeichnung liegt, hat diese Methode sogar gewisse Vorteile. Dabei ist zu berücksichtigen, dass sich die mit dieser Methode durchgeführten Bauten oft als „überfüllt“ erweisen. Dennoch erweist sich in manchen Fällen die Methode der Hilfsabschnitte als die rationalste.

Kombinierte Methode

Das Wesentliche der kombinierten Methode zur Konstruktion von Polyederabschnitten ist die Anwendung von Theoremen über die Parallelität von Linien und Ebenen im Raum in Kombination mit der axiomatischen Methode.

Koordinatenmethode zum Konstruieren von Abschnitten.

Der Kern der Koordinatenmethode besteht darin, die Koordinaten der Schnittpunkte von Kanten oder eines Polyeders mit einer Sekantenebene zu berechnen, die durch die Gleichung der Ebene gegeben sind. Die Gleichung der Schnittebene wird basierend auf den Bedingungen des Problems berechnet.

Notiz dass diese Methode zur Konstruktion eines Abschnitts eines Polyeders für einen Computer akzeptabel ist, da sie mit einem großen Berechnungsaufwand verbunden ist und es daher ratsam ist, diese Methode mithilfe eines Computers durchzuführen.

Unsere Hauptaufgabe wird darin bestehen, einen Abschnitt eines Polyeders mit einer Ebene zu konstruieren, d. h. bei der Konstruktion des Schnittpunkts dieser beiden Mengen.

Konstruktion von Polyederabschnitten

Zunächst stellen wir fest, dass der Abschnitt eines konvexen Polyeders ein konvexes flaches Polygon ist, dessen Eckpunkte im allgemeinen Fall die Schnittpunkte der Sekantenebene mit den Kanten des Polyeders und der Seiten mit seinen Flächen sind.

Beispiele für die Abschnittserstellung:

Es gibt viele verschiedene Möglichkeiten, einen Abschnitt zu definieren. Am gebräuchlichsten ist die Methode, eine Schnittebene durch drei Punkte festzulegen, die nicht auf einer Geraden liegen.

Beispiel 1 Für Box ABCDA 1 B 1 C 1 D 1 . Konstruieren Sie einen Abschnitt, der durch die Punkte M, N, L verläuft.

Lösung:

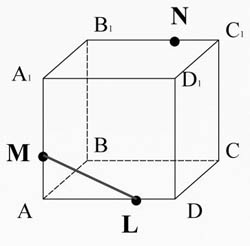
Verbinde die Punkte M und L, die in der Ebene AA liegen 1 D 1 D.

Schneiden Sie die Linie ML (die zum Abschnitt gehört) mit der Kante A 1 D 1 1 D 1 D. Holen Sie sich Punkt X 1 .

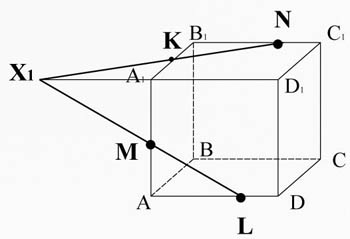
Der Punkt X1 liegt auf der Kante A 1 D 1 , und daher die Ebenen A 1 B 1 C 1 D 1 , verbinde es mit einem Punkt N, der in derselben Ebene liegt.

X 1 N schneidet Kante A 1 B 1 am Punkt K.

Verbinde die Punkte K und M, die in derselben Ebene AA liegen 1 B 1 B.

Finden Sie die Schnittlinie der Schnittebene mit der Ebene DD 1 C 1 C:

Schneiden Sie die Linie ML (die zum Abschnitt gehört) mit der Kante DD 1 , sie liegen in der gleichen Ebene AA 1 D 1 D, erhalte Punkt X 2 .

Lassen Sie uns die Linie KN (die zum Abschnitt gehört) mit der Kante D schneiden 1 C 1 , sie liegen in derselben Ebene A 1 B 1 C 1 D 1 , wir erhalten den Punkt X3;

Die Punkte X2 und X3 liegen in der Ebene DD 1 C 1 C. Zeichnen Sie eine Linie X 2 X 3 , die die Kante C schneidet 1 C am Punkt T und die Kante DC am Punkt P. Und verbinden wir die Punkte L und P, die in der Ebene ABCD liegen.

Somit gilt das Problem als gelöst, wenn alle Segmente gefunden werden, entlang derer die Ebene die Flächen des Polyeders schneidet, was wir getan haben. MKNTPL – gewünschter Abschnitt.

Notiz. Die gleiche Aufgabe zur Konstruktion eines Schnittes lässt sich mit der Eigenschaft paralleler Ebenen lösen.

Aus dem oben Gesagten können wir einen Algorithmus (Regel) zur Lösung von Problemen dieser Art zusammenstellen.

Regeln für die Konstruktion von Polyederabschnitten:

Beispiel 2 DL, M

Wir lösen nach der axiomatischen Methode:

Zeichnen Sie eine HilfsebeneDKM, die die Kanten AB und BC in den Punkten E und schneidetF(Der Lösungsverlauf ist in Abb. 2 dargestellt.) Lassen Sie uns eine „Spur“ des CM der Schnittebene auf dieser Hilfsebene erstellen und den Schnittpunkt von CM und E findenF- Punkt P. Punkt P, sowieL, liegt in der Ebene ABC, und es ist möglich, eine Gerade zu zeichnen, entlang der die Schnittebene die Ebene ABC schneidet („Spur“ des Schnitts in der Ebene ABC).

Beispiel 3 Auf den Kanten AB und AD der Pyramide MABCD setzen wir die Punkte P bzw. Q, die Mittelpunkte dieser Kanten, und auf der Kante MC setzen wir den Punkt R. Konstruieren wir einen Abschnitt der Pyramide durch eine vorbeiziehende Ebene durch die Punkte P, Q und R.

Die Lösung erfolgt durch eine kombinierte Methode:

1). Es ist klar, dass die Hauptspur der Ebene PQR die Linie PQ ist.

2). Finden Sie den Punkt K, an dem die MAC-Ebene die Linie PQ schneidet. Die Punkte K und R gehören sowohl zur PQR-Ebene als auch zur MAC-Ebene. Wenn wir also die Gerade KR zeichnen, erhalten wir die Schnittlinie dieser Ebenen.

3). Suchen wir den Punkt N=AC BD, zeichnen wir die Linie MN und finden wir den Punkt F=KR MN.

4). Punkt F ist gemeinsamer Punkt Ebenen PQR und MDB, das heißt, diese Ebenen schneiden sich entlang einer geraden Linie, die durch den Punkt F verläuft. Da PQ gleichzeitig die Mittellinie des Dreiecks ABD ist, ist PQ parallel zu BD, das heißt, die Linie PQ ist es auch parallel zur Ebene MDB. Dann schneidet die durch die Linie PQ verlaufende Ebene PQR die Ebene MDB entlang der Linie parallel zur Linie PQ, also parallel zur Linie BD. Daher zeichnen wir in der Ebene MDB durch den Punkt F eine Linie parallel zur Linie BD.

5). Weitere Konstruktionen sind aus der Abbildung ersichtlich. Als Ergebnis erhalten wir das Polygon PQD „RB“ – den erforderlichen Abschnitt

Betrachten Sie die Abschnitte des Prismas Betrachten Sie der Einfachheit halber, also der Bequemlichkeit des logischen Denkens, die Abschnitte des Würfels (Abb. 3.a):

Reis. 3.a

Abschnitte des Prismas durch Ebenen parallel zu den Seitenkanten sind Parallelogramme. Insbesondere Diagonalschnitte sind Parallelogramme (Abb. 4).

Def. Diagonalabschnitt Ein Prisma ist ein Schnitt durch eine Ebene, die durch zwei Seitenkanten verläuft, die nicht zur selben Fläche gehören.

Das aus einem Diagonalschnitt eines Prismas resultierende Polygon ist ein Parallelogramm. Frage zur Anzahl der DiagonalabschnitteN-Winkelprisma ist schwieriger als die Frage nach der Anzahl der Diagonalen. Es wird so viele Abschnitte geben, wie Diagonalen an der Basis vorhanden sind. Wir wissen, dass ein konvexes Prisma an seiner Basis konvexe Polygone hat, während ein konvexesN-gon der Diagonalen. Man kann also sagen, dass es halb so viele Diagonalabschnitte wie Diagonalen gibt.

Notiz: Bei der Konstruktion von Abschnitten eines Parallelepipeds in der Abbildung sollte die Tatsache berücksichtigt werden, dass, wenn die Schnittebene entlang einiger Segmente zwei gegenüberliegende Flächen schneidet, diese Segmente „durch die Eigenschaft des Parallelepipeds parallel sind, d.h. Gegenüberliegende Flächen eines Parallelepipeds sind parallel und gleich.

Wir geben Antworten auf häufig gestellte Fragen:

Welche Polygone erhält man im Schnitt eines Würfels durch eine Ebene?

„Dreieck, Viereck, Fünfeck, Sechseck“.

Kann ein ebener Würfelquerschnitt ein Siebeneck ergeben? Und das Achteck?

"kann nicht".

3) Es stellt sich die Frage: Was ist die größte Anzahl von Seiten eines Polygons, die man durch einen Schnitt eines Polyeders mit einer Ebene erhält?

Größte Zahl Seiten des Polyeders, die im Abschnitt des Polyeders durch die Ebene erhalten werden, sind gleich der Anzahl der Flächen des Polyeders .

Beispiel 3 Konstruieren Sie einen Abschnitt von Prisma A 1 B 1 C 1 D 1 ABCD durch eine Ebene, die durch drei Punkte M, N, K verläuft.

Betrachten Sie den Fall der Lage der Punkte M, N, K auf der Oberfläche eines Prismas (Abb. 5).

Betrachten Sie den Fall: In diesem Fall ist es offensichtlich, dass M1 = B1.

Gebäude:

Beispiel 4 Konstruieren Sie einen Abschnitt des Parallelepipeds ABCDA 1 B 1 C 1 D 1 eine Ebene, die durch die Punkte M, N, P verläuft (die Punkte sind in der Zeichnung angegeben (Abb. 6)).

Lösung:

Reis. 6

Die Punkte N und P liegen in der Schnittebene und in der Ebene der unteren Basis des Parallelepipeds. Konstruieren wir eine Linie, die durch diese Punkte verläuft. Diese Linie ist die Spur der Sekantenebene auf der Basisebene des Parallelepipeds.

Setzen wir die Linie fort, auf der die Seite AB des Parallelepipeds liegt. Die Geraden AB und NP schneiden sich in einem Punkt S. Dieser Punkt gehört zur Schnittebene.

Denn auch der Punkt M gehört zur Schnittebene und schneidet die Gerade AA 1 irgendwann x.

Die Punkte X und N liegen in derselben Ebene der Fläche AA 1 D 1 D, verbinde sie und erhalte die Leitung XN.

Da die Ebenen der Flächen des Parallelepipeds parallel sind, ist es möglich, eine gerade Linie durch den Punkt M in der Fläche A zu zeichnen 1 B 1 C 1 D 1 parallel zur Linie NP. Diese Linie schneidet Seite B 1 MIT 1 am Punkt Y.

Ebenso zeichnen wir die Linie YZ parallel zur Linie XN. Wir verbinden Z mit P und erhalten den gewünschten Abschnitt – MYZPNX.

Abschnitte der Pyramide durch Ebenen, die durch ihre Spitze verlaufen, sind Dreiecke. Diagonalabschnitte sind insbesondere Dreiecke. Dabei handelt es sich um Schnitte durch Ebenen, die durch zwei nicht benachbarte Seitenkanten der Pyramide verlaufen.

Beispiel 4 Konstruieren Sie einen Abschnitt der Pyramide ABCDeine Ebene, die durch die Punkte K geht,L, M.

Lösung:

Lassen Sie uns dasselbe Beispiel anders lösen. .

Nehmen wir an, dass für die Punkte KL, und М der AbschnittKLNM(Abb. 7). Bezeichnen Sie mitFder Schnittpunkt der Diagonalen des VierecksKLNM. Zeichnen wir eine gerade LinieD.F.und bezeichnen mitF 1 sein Schnittpunkt mit der Fläche ABC. PunktF 1 fällt mit dem Schnittpunkt der Geraden AM und SK zusammen (F 1 gehört gleichzeitig zu den Ebenen AMDUndDSC). PunktF 1 einfach zu bauen. Als nächstes bauen wir einen PunktFals SchnittpunktD.F. 1 UndLM. Als nächstes finden wir den PunktN.

Die betrachtete Methode wird aufgerufenInterne Designmethode . (Für unseren Fall wir redenüber zentrales Design. ViereckKISA ist die Projektion eines VierecksKMNLvon einem PunktD. In diesem Fall der Schnittpunkt der DiagonalenKMNL- PunktF- geht zum Schnittpunkt der Diagonalen des VierecksKISA - PunktF 1 .

Schnittfläche eines Polyeders.

Das Problem der Berechnung der Querschnittsfläche eines Polyeders wird meist in mehreren Schritten gelöst. Wenn das Problem besagt, dass der Schnitt erstellt wird (oder dass die Schnittebene gezeichnet wird usw.), dann wird im ersten Schritt der Lösung die Form der im Schnitt erhaltenen Figur ermittelt.

Dies muss erfolgen, um die geeignete Formel zur Berechnung der Querschnittsfläche auszuwählen. Nachdem die Form der im Abschnitt erhaltenen Figur geklärt und die Formel zur Berechnung der Fläche dieser Figur ausgewählt wurde, geht es direkt mit der Rechenarbeit weiter.

In manchen Fällen kann es einfacher sein, wenn wir, ohne die Form der im Abschnitt erhaltenen Figur herauszufinden, sofort mit der Berechnung ihrer Fläche nach der Formel fortfahren, die sich aus dem Satz ergibt.

Der Satz über die Fläche der orthogonalen Projektion eines Polygons: Die Fläche der orthogonalen Projektion eines Polygons auf eine Ebene ist gleich dem Produkt seiner Fläche und dem Kosinus des Winkels zwischen der Ebene des Polygons und der Projektionsebene: .

Eine gültige Formel zur Berechnung der Querschnittsfläche lautet: Dabei ist die Fläche der orthogonalen Projektion der im Schnitt erhaltenen Figur und der Winkel zwischen der Sekantenebene und der Ebene, auf die die Figur projiziert wird. Bei einer solchen Lösung ist es notwendig, eine orthogonale Projektion der im Schnitt erhaltenen Figur zu konstruieren und zu berechnen

Wenn die Bedingung des Problems besagt, dass der Abschnitt gebaut werden muss und die Fläche des erhaltenen Abschnitts ermittelt werden soll, dann ist es in der ersten Phase sinnvoll, den gegebenen Abschnitt zu bauen und dann natürlich die Form zu bestimmen die im Abschnitt erhaltene Zahl usw.

Wir stellen folgende Tatsache fest: Da Abschnitte aus konvexen Polyedern konstruiert werden, ist das Abschnittspolygon auch konvex, sodass seine Fläche durch Teilen in Dreiecke ermittelt werden kann, d. h. die Abschnittsfläche ist gleich der Summe der Flächen der Dreiecke, aus denen es besteht.

Aufgabe 1.

– richtig Dreieckige Pyramide mit einer Basisseite, die gleich und gleich einer Höhe ist. Konstruieren Sie einen Abschnitt der Pyramide durch eine Ebene, die durch die Punkte geht, wo sich der Mittelpunkt der Seite befindet, und ermitteln Sie deren Fläche (Abb. 8).

Lösung.

Der Querschnitt der Pyramide ist ein Dreieck. Lassen Sie uns seinen Bereich finden.

Da die Basis der Pyramide ein gleichseitiges Dreieck ist und der Punkt der Mittelpunkt der Seite ist, ist es die Höhe und dann .

Die Fläche eines Dreiecks lässt sich ermitteln:

Aufgabe 2.

Seitliche Rippe eines regelmäßigen Prismas ist gleich der Seite der Grundfläche. Konstruieren Sie Abschnitte eines Prismas durch Ebenen, die durch einen Punkt verlaufenA, senkrecht zur Linie Wenn Sie die Fläche des resultierenden Abschnitts des Prismas ermitteln.

Lösung.

Lassen Sie uns den angegebenen Abschnitt erstellen. Machen wir dies beispielsweise aus rein geometrischen Überlegungen wie folgt.

In einer Ebene, die durch eine bestimmte Linie und einen bestimmten Punkt verläuft, zeichnen wir eine Linie durch diesen Punkt senkrecht zur Linie (Abb. 9). Nutzen wir zu diesem Zweck die Tatsache, dass im Dreieck das heißt, sein Median ist auch die Höhe dieses Dreiecks. Also eine gerade Linie.

Durch den Punkt ziehen wir eine weitere Linie senkrecht zur Linie. Zeichnen wir es zum Beispiel in einer Ebene, die durch eine Gerade geht. Es ist klar, dass diese Linie eine Linie ist

Es werden also zwei Schnittlinien senkrecht zur Linie konstruiert. Diese Linien definieren eine Ebene, die durch einen Punkt senkrecht zur Linie verläuft, d. h. es ist eine Sekantenebene gegeben.

Aus dieser Ebene konstruieren wir einen Abschnitt des Prismas. Beachten Sie, dass die Linie parallel zur Ebene verläuft. Dann schneidet die durch die Linie verlaufende Ebene die Ebene entlang einer Linie parallel zur Linie, also der Linie. Zeichnen Sie eine gerade Linie durch den Punkt und verbinden Sie den resultierenden Punkt mit einem Punkt.

Viereck gegebener Abschnitt. Lassen Sie uns seine Fläche bestimmen.

Es ist klar, dass ein Viereck ein Rechteck ist, also seine Fläche

Reis. 9

KONSTRUKTION VON ABSCHNITT UND ABSCHNITT AUF ZEICHNUNGEN

Die Zeichnung des Teils entsteht durch sequentielles Hinzufügen der erforderlichen Vorsprünge, Schnitte und Abschnitte. Zunächst wird eine benutzerdefinierte Ansicht mit einem benutzerdefinierten Modell erstellt und die Modellausrichtung wird so eingestellt, dass sie am besten zur Hauptansicht passt. Darüber hinaus werden für diesen und die folgenden Typen die notwendigen Schnitte und Abschnitte erstellt.

Die Hauptansicht (Vorderansicht) ist so gewählt, dass sie eine möglichst vollständige Vorstellung von den Formen und Abmessungen des Teils vermittelt.

Abschnitte in Zeichnungen

Abhängig von der Lage der Schnittebene werden folgende Schnittarten unterschieden:

A) horizontal, wenn die Schnittebene parallel zur horizontalen Projektionsebene verläuft;

B) vertikal, wenn die Schnittebene senkrecht zur horizontalen Projektionsebene steht;

C) geneigt – die Schnittebene ist zu den Projektionsebenen geneigt.

Vertikale Abschnitte sind unterteilt in:

· frontal – die Schnittebene verläuft parallel zur frontalen Projektionsebene;

· Profil – Schnittebene ist parallel zur Profilprojektionsebene.
Abhängig von der Anzahl der Schnittebenen ergeben sich folgende Schnitte:

· einfach - mit einer Schnittebene (Abb. 107);

· komplex - mit zwei oder mehr Schnittebenen (Abb. 108)
Die Norm sieht folgende Arten komplexer Schnitte vor:

· gestuft, wenn die Sekantenebenen parallel sind (Abb. 108 a) und gestrichelte Linien - die Sekantenebenen schneiden sich (Abb. 108 b)

Abb.107 Einfacher Schnitt

A) b)

Abb.108 Komplexe Schnitte

Bezeichnung von Schnitten

Wenn in einem einfachen Schnitt die Sekantenebene mit der Symmetrieebene des Objekts zusammenfällt, wird der Schnitt nicht angezeigt (Abb. 107). In allen anderen Fällen werden die Abschnitte durch Großbuchstaben des russischen Alphabets gekennzeichnet, beginnend mit dem Buchstaben A, zum Beispiel A-A.

Die Position der Schnittebene in der Zeichnung wird durch die Schnittlinie angezeigt – eine verdickte offene Linie. Bei einem komplexen Schnitt werden auch Striche an den Wendepunkten der Schnittlinie ausgeführt. Pfeile, die die Blickrichtung anzeigen, sollten auf den Anfangs- und Endstrichen platziert werden, die Pfeile sollten einen Abstand von 2-3 mm von den äußeren Enden der Striche haben. Auf der Außenseite jedes Pfeils, der die Blickrichtung anzeigt, ist derselbe Großbuchstabe angebracht.

Die gleiche Schaltfläche wird zur Bezeichnung von Schnitten und Abschnitten im KOMPAS-System verwendet Schnittlinie auf der Legendenseite (Abb. 109).

Abb.109 Schaltfläche „Schnittlinie“.

Halbansicht mit Halbschnitt verbinden

Wenn die Ansicht und der Schnitt symmetrische Figuren sind (Abb. 110), können Sie die Hälfte der Ansicht und die Hälfte des Schnitts verbinden und sie durch eine strichpunktierte dünne Linie, die die Symmetrieachse darstellt, trennen. Ein Teil des Abschnitts wird normalerweise rechts von der Symmetrieachse platziert, die den Teil der Ansicht vom Teil des Abschnitts trennt, oder unterhalb der Symmetrieachse. Versteckte Konturlinien an den verbundenen Teilen der Ansicht und des Schnitts werden normalerweise nicht angezeigt. Wenn die axiale Linie, die die Ansicht und den Schnitt trennt, mit der Projektion einer Linie zusammenfällt, beispielsweise der Kante einer facettierten Figur, dann werden die Ansicht und der Schnitt durch eine durchgezogene Wellenlinie getrennt, die links von der Symmetrieachse gezeichnet wird Die Kante liegt auf der Innenfläche oder rechts, wenn die Kante außen ist.

Reis. 110 Teil einer Ansicht und eines Abschnitts verbinden

Baukürzungen

Wir werden die Konstruktion von Abschnitten im KOMPAS-System am Beispiel der Konstruktion einer Prismenzeichnung untersuchen, deren Aufgabe in Abb. 111 dargestellt ist.

Der Ziehungsablauf ist wie folgt:

1. Von angegebenen Abmessungen Lassen Sie uns ein solides Modell eines Prismas erstellen (Abb. 109 b). Speichern wir das Modell im Speicher des Computers in einer Datei mit dem Namen „Prism“.

Abb. 112 Linienfeld

3. So erstellen Sie einen Profilabschnitt (Abb. 113) zeichne eine Linie Abschnitt A-A in der Hauptansicht über die Schaltfläche Schnittlinie.

Abb.113 Aufbau eines Profilabschnitts

Die Blickrichtung und der Text der Bezeichnung können am Bedienfeld mit dem Befehl am unteren Bildschirmrand ausgewählt werden (Abb. 114). Die Konstruktion der Schnittlinie wird durch Klicken auf die Schaltfläche „Objekt erstellen“ abgeschlossen.

Abb.114 Bedienfeld für den Befehl zum Erstellen von Schnitten und Abschnitten

4. Wählen Sie im Bedienfeld „Assoziative Ansichten“ (Abb. 115) die Schaltfläche „Schnittlinie“ und geben Sie dann die Schnittlinie mit der auf dem Bildschirm angezeigten Überfüllung an. Wenn alles richtig gemacht ist (die Schnittlinie muss in der aktiven Ansicht gezeichnet werden), wird die Schnittlinie rot. Nach Angabe der Schnittlinie A-A erscheint auf dem Bildschirm ein Bildphantom in Form eines gesamten Rechtecks.

Abb. 115 Bedienfeld „Assoziative Ansichten“.

Mit Hilfe des Schalters „Schnitt/Schnitt“ in der Eigenschaftsleiste wird der Bildtyp „Schnitt“ (Abb. 116) und der Maßstab des angezeigten Schnitts ausgewählt.

Abb.116 Bedienfeld für den Befehl zum Erstellen von Schnitten und Abschnitten

Der Profilabschnitt wird automatisch im Projektionsanschluss und mit einer Standardnotation erstellt. Bei Bedarf kann die Projektionsverbindung über den Schalter ausgeschaltet werden Projektionsanschluss (Abb. 116). Um die Schraffurparameter festzulegen, die im erstellten Abschnitt (Abschnitt) verwendet werden, verwenden Sie die Steuerelemente auf der Registerkarte Schraffur.

Abb.117 Konstruktion eines horizontalen Abschnitts B-B und Abschnitt C-C

Wenn die gewählte Schnittebene bei der Schnittkonstruktion mit der Symmetrieebene des Teils übereinstimmt, ist ein solcher Schnitt laut Norm nicht angegeben. Wenn Sie jedoch einfach die Abschnittsbezeichnung löschen, wird aufgrund der Tatsache, dass die Ansicht und der Abschnitt im Speicher des Computers miteinander verbunden sind, der gesamte Abschnitt gelöscht. Um die Bezeichnung zu entfernen, müssen Sie daher zunächst die Verbindung zwischen der Ansicht und dem Abschnitt zerstören. Klicken Sie dazu mit der linken Maustaste, um den Abschnitt auszuwählen, und klicken Sie dann mit der rechten Maustaste, um das Kontextmenü zu öffnen, in dem der Eintrag „Ansicht zerstören“ ausgewählt wird (Abb. 97). Das Abschnittssymbol kann nun gelöscht werden.

5. Um einen horizontalen Schnitt zu konstruieren, zeichnen wir in der Vorderansicht eine B-B-Schnittlinie durch die untere Ebene des Lochs. Die Vorderansicht muss zunächst durch zwei Klicks mit der linken Maustaste aktuell gemacht werden. Anschließend wird ein horizontaler Abschnitt erstellt (Abb. 117).

6. Bei der Konstruktion eines Frontalschnitts sind ein Teil der Ansicht und ein Teil des Schnitts kompatibel, weil es sind symmetrische Figuren. Der äußere Rand des Prismas wird auf die Trennlinie zwischen Ansicht und Schnitt projiziert, also grenzen wir ab Ansicht und Schnitt einer durchgezogenen dünnen Wellenlinie, die rechts von der Symmetrieachse gezeichnet ist, weil äußere Rippe. Mit der Schaltfläche können Sie eine Wellenlinie zeichnen. Bezier-Kurve im Bedienfeld „Geometrie“, gezeichnet mit dem Linienstil „Für Schnitt“ (Abb. 118). Geben Sie nacheinander die Punkte an, durch die die Bezier-Kurve verlaufen soll. Um die Befehlsausführung abzuschließen, klicken Sie auf die Schaltfläche Objekt erstellen.

Abb.118 Auswahl eines Linienstils für einen Bruch

Schnitt

Ein Schnitt ist ein Bild eines Objekts, das durch mentales Zerlegen eines Objekts mit einer Ebene entsteht. Der Schnitt zeigt nur, was sich in der Schnittebene befindet.

Die Lage der Schnittebene, mit der der Schnitt gebildet wird, wird in der Zeichnung wie bei Schnitten durch die Schnittlinie angezeigt.

Abschnitte werden je nach Position in den Zeichnungen in erweiterte und überlagerte Abschnitte unterteilt. Die entfernten Abschnitte befinden sich meist im freien Feld der Zeichnung und werden durch die Hauptlinie umrandet. Die überlagerten Ausschnitte werden direkt auf das Bild des Objekts gelegt und mit dünnen Linien umrandet (Abb. 119).

Abb.119 Konstruktion von Abschnitten

Betrachten Sie die Reihenfolge der Konstruktion einer Zeichnung eines Prismas mit verlängerter Schräge Abschnitt B-B(Abb. 117).

1. Aktivieren Sie die Vorderansicht, indem Sie mit der linken Maustaste auf die Ansicht doppelklicken und mit der Schaltfläche eine Schnittlinie zeichnen Schnitt Linie . Wählen wir den Text der Inschrift В-В aus.

2. Geben Sie mit der Schaltfläche „Schnittlinie“ im Bedienfeld „Assoziative Ansichten“ (Abb. 115), die als Überfüllung erscheint, die Schnittlinie an Flugzeuge B-B. Wählen Sie mit dem Schalter „Schnitt/Schnitt“ in der Eigenschaftsleiste den Bildtyp „Schnitt“ (Abb. 116). Der Maßstab des angezeigten Ausschnitts wird im Fenster „Skalierung“ ausgewählt.

Der konstruierte Abschnitt befindet sich in einer Projektionsbeziehung, die seine Bewegung in der Zeichnung einschränkt. Die Projektionsbeziehung kann jedoch über die Schaltfläche deaktiviert werden Projektionsanschluss.

Zeichnen Sie auf der fertigen Zeichnung Mittellinien Geben Sie ggf. die Abmessungen ein.

Die Aufgaben zum Konstruieren von Abschnitten von Polyedern dauern bedeutender Ort als Schulgeometriekurs für das Gymnasium und bei Prüfungen auf verschiedenen Niveaus. Die Lösung dieser Art von Problemen trägt zur Aneignung der Axiome der Stereometrie, zur Systematisierung von Wissen und Fähigkeiten sowie zur Entwicklung bei räumliche Darstellung und konstruktive Fähigkeiten. Schwierigkeiten, die bei der Lösung von Problemen beim Bau von Abschnitten auftreten, sind allgemein bekannt.

Von dem frühe Kindheit wir stehen vor Einschnitten. Wir schneiden Brot, Wurst und andere Produkte, schneiden mit einem Messer einen Stock oder Bleistift. Die Sekantenebene ist in all diesen Fällen die Messerebene. Abschnitte (Stückabschnitte) sind unterschiedlich.

Der Abschnitt eines konvexen Polyeders ist ein konvexes Polygon, dessen Eckpunkte im allgemeinen Fall die Schnittpunkte der Schnittebene mit den Kanten des Polygons und die Seiten die Schnittlinien der Schnittebene mit sind die Gesichter.

Um eine Schnittlinie zweier Ebenen zu konstruieren, reicht es aus, zwei gemeinsame Punkte dieser Ebenen zu finden und eine Linie durch sie zu ziehen. Dem liegen folgende Aussagen zugrunde:

1. Wenn zwei Punkte einer Geraden zu einer Ebene gehören, dann gehört die gesamte Gerade zu dieser Ebene;

2. Wenn zwei verschiedene Ebenen einen gemeinsamen Punkt haben, dann schneiden sie sich entlang einer Geraden, die durch diesen Punkt verläuft.

Wie ich bereits sagte, kann die Konstruktion von Polyederabschnitten auf der Grundlage der Axiome der Stereometrie und der Sätze über die Parallelität von Linien und Ebenen erfolgen. Gleichzeitig gibt es bestimmte Methoden zur Konstruktion ebener Polyederabschnitte. Die folgenden drei Methoden sind am effektivsten:

Trace-Methode

Interne Designmethode

Kombinierte Methode.

Beim Studium der Geometrie und insbesondere derjenigen Abschnitte davon, in denen Bilder betrachtet werden geometrische Formen, Bilder von geometrischen Formen helfen bei der Verwendung von Computerpräsentationen. Mit Hilfe eines Computers werden viele Geometriestunden anschaulicher und dynamischer. Axiome, Theoreme, Beweise, Konstruktionsaufgaben, Abschnittskonstruktionsaufgaben können durch aufeinanderfolgende Konstruktionen auf dem Bildschirm begleitet werden. Computergenerierte Zeichnungen können gespeichert und in andere Dokumente eingefügt werden.

Ich möchte ein paar Folien zum Thema zeigen: „Konstruktion von Abschnitten in.“ geometrische Körper»

Um den Schnittpunkt einer Linie und einer Ebene zu konstruieren, suchen Sie eine Linie in der Ebene, die die gegebene Linie schneidet. Dann ist der gesuchte Punkt der Schnittpunkt der gefundenen Geraden mit der gegebenen. Sehen wir es uns auf den nächsten Folien an.

Aufgabe 1.

An den Kanten des Tetraeders DABC sind zwei Punkte M und N markiert; M GAD, N b DC. Wählen Sie den Schnittpunkt der Linie MN mit der Basisebene.

Lösung: um den Schnittpunkt der Geraden MN mit der Ebene zu finden

Basis werden wir AC und Segment MN weiterführen. Markieren wir den Schnittpunkt dieser Geraden durch X. Der Punkt X gehört zur Geraden MN und der Fläche AC, und AC liegt in der Basisebene, was bedeutet, dass der Punkt . Daher ist der Punkt X der Schnittpunkt der Linie MN mit der Basisebene.

Betrachten wir das zweite Problem. Machen wir es etwas komplizierter.

Aufgabe 2.

Gegeben sei ein Tetraeder DABC der Punkte M und N, wobei M € DA, N C (DBC). Finden Sie den Schnittpunkt der Linie MN mit der Ebene ABC.

Lösung: Der Schnittpunkt der Geraden MN mit der Ebene ABC muss in der Ebene, die die Gerade MN enthält, und in der Ebene der Grundfläche liegen. Wir setzen das Segment DN bis zum Schnittpunkt mit der Kante DC fort. Wir markieren den Schnittpunkt durch E. Wir setzen die Linien AE und MN bis zu ihrem Schnittpunkt fort. Beachten Sie X. Der Punkt X gehört zu MN, liegt also auf der Ebene, die die Gerade MN enthält, und X gehört zu AE, und AE liegt auf der Ebene ABC. Also liegt auch X in der Ebene ABC. Daher ist X der Schnittpunkt der Geraden MN und der Ebene ABC.

Machen wir die Aufgabe komplizierter. Betrachten Sie einen Schnitt geometrischer Figuren anhand von Ebenen, die durch drei gegebene Punkte verlaufen.

Aufgabe 3

Auf den Kanten AC, AD und DB des Tetraeders DABC sind die Punkte M, N und P markiert. Konstruieren Sie einen Abschnitt des Tetraeders durch die Ebene MNP.

Lösung: Konstruieren Sie eine Gerade, entlang der die Ebene MNP verläuft. Schneidet die Gesichtsebene ABC. Punkt M ist ein gemeinsamer Punkt dieser Ebenen. Um einen weiteren gemeinsamen Punkt aufzubauen, führen wir die Segmente AB und NP fort. Wir markieren den Schnittpunkt durch X, der der zweite gemeinsame Punkt der Ebenen MNP und ABC sein wird. Diese Ebenen schneiden sich also entlang der Geraden MX. MX schneidet die Kante BC an einem Punkt E. Da E auf MX liegt und MX eine Gerade ist, die zur Ebene MNP gehört, folgt daraus, dass PE zu MNP gehört. Der viereckige MNPE ist der erforderliche Abschnitt.

Aufgabe 4

Wir konstruieren einen Abschnitt eines geraden Prismas ABCA1B1C1 durch eine Ebene, die durch die Punkte P verläuft , Q,R, wobei R zu ( AA 1C 1C), R gehört IN 1C1,

Q gehört zu AB

Lösung: Alle drei Punkte P,Q,R liegen in verschiedenen Flächen, daher können wir noch keine Schnittlinie der Sekantenebene mit irgendeiner Fläche des Prismas konstruieren. Finden wir den Schnittpunkt von PR mit ABC. Finden wir die Projektionen der Punkte P und R auf die Basisebene PP1 senkrecht zu BC und RR1 senkrecht zu AC. Die Linie P1R1 schneidet die Linie PR im Punkt X. X ist der Schnittpunkt der Linie PR mit der Ebene ABC. Er liegt in der gewünschten Ebene K und in der Ebene der Basis, wie der Punkt Q. XQ ist eine Gerade, die K mit der Ebene der Basis schneidet. XQ schneidet AC im Punkt K. Daher ist KQ das Segment des Schnittpunkts der Ebene X mit der Fläche ABC. K und R liegen in der X-Ebene und in der Ebene der AA1C1C-Fläche. Zeichnen Sie eine Linie KR und markieren Sie den Schnittpunkt mit A1Q E. KE ist die Schnittlinie der Ebene X mit dieser Fläche. Finden Sie die Schnittlinie der X-Ebene mit der Ebene der Flächen BB1A1A. KE schneidet A1A im Punkt Y. Die Linie QY ist die Schnittlinie der Sekantenebene mit der Ebene AA1B1B. FPEKQ – gewünschter Abschnitt.

Aufgaben zum Konstruieren von Würfelabschnitten durch eine Ebene sind in der Regel einfacher als beispielsweise Aufgaben für Pyramidenabschnitte.

Wir können eine Linie durch zwei Punkte ziehen, wenn sie in derselben Ebene liegen. Beim Konstruieren von Würfelschnitten ist eine weitere Möglichkeit zum Konstruieren einer Spur einer Schnittebene möglich. Da die dritte Ebene zwei parallele Ebenen entlang paralleler gerader Linien schneidet, können wir eine gerade Linie zeichnen, wenn in einer der Flächen bereits eine gerade Linie erstellt wurde und es in der anderen einen Punkt gibt, durch den der Abschnitt verläuft dieser Punkt parallel zum angegebenen.

Überlegen Sie weiter konkrete Beispiele wie man durch eine Ebene Abschnitte eines Würfels konstruiert.

1) Konstruieren Sie einen Abschnitt des Würfels durch eine Ebene, die durch die Punkte A, C und M verläuft.

Probleme dieser Art sind die einfachsten aller Probleme zur Konstruktion von Würfelabschnitten. Da die Punkte A und C in derselben Ebene (ABC) liegen, können wir eine Linie durch sie ziehen. Seine Spur ist das Segment AC. Es ist unsichtbar, daher stellen wir AC mit einem Strich dar. Ebenso verbinden wir die Punkte M und C, die in derselben Ebene liegen (CDD1), und die Punkte A und M, die in derselben Ebene liegen (ADD1). Dreieck ACM ist der erforderliche Abschnitt.

2) Konstruieren Sie einen Abschnitt des Würfels durch eine Ebene, die durch die Punkte M, N, P verläuft.

Hier liegen nur die Punkte M und N in derselben Ebene (ADD1), also ziehen wir eine Gerade durch sie und erhalten die Spur MN (unsichtbar). Da die gegenüberliegenden Flächen des Würfels in parallelen Ebenen liegen, schneidet die Schnittebene die parallelen Ebenen (ADD1) und (BCC1) entlang paralleler Linien. Eine der Parallelstrecken haben wir bereits gebaut – das ist MN.

Durch den Punkt P ziehen wir eine Linie parallel zu MN. Es schneidet die Kante BB1 im Punkt S. PS ist die Spur der Sekantenebene in der Fläche (BCC1).

Wir zeichnen eine Gerade durch die Punkte M und S, die in derselben Ebene (ABB1) liegen. Habe die MS-Spur erhalten (sichtbar).

Die Ebenen (ABB1) und (CDD1) sind parallel. Es gibt bereits eine Linie MS in der Ebene (ABB1), also zeichnen wir durch den Punkt N in der Ebene (CDD1) eine Linie parallel zu MS. Diese Linie schneidet die Kante D1C1 im Punkt L. Ihre Spur ist NL (unsichtbar). Die Punkte P und L liegen in derselben Ebene (A1B1C1), also ziehen wir eine gerade Linie durch sie.

Das Fünfeck MNLPS ist der erforderliche Abschnitt.

3) Konstruieren Sie einen Abschnitt des Würfels durch eine Ebene, die durch die Punkte M, N, P verläuft.

Die Punkte M und N liegen in derselben Ebene (BCC1), sodass eine gerade Linie durch sie gezogen werden kann. Wir erhalten die Spur MN (sichtbar). Die Ebene (BCC1) ist parallel zur Ebene (ADD1), also ziehen wir durch den in (ADD1) liegenden Punkt P eine Linie parallel zu MN. Es schneidet die Kante AD im Punkt E. Wir haben die Spur PE (unsichtbar) erhalten.

Es gibt keine Punkte mehr, die in derselben Ebene liegen, oder eine Linie und ein Punkt in parallelen Ebenen. Daher muss eine der bereits bestehenden Linien fortgeführt werden, um einen zusätzlichen Punkt zu erhalten.

Wenn wir die Linie MN fortsetzen, müssen wir, da sie in der Ebene (BCC1) liegt, nach dem Schnittpunkt von MN mit einer der Linien dieser Ebene suchen. Es gibt bereits Schnittpunkte mit CC1 und B1C1 – das sind M und N. Es bleiben die Linien BC und BB1 übrig. Wir setzen BC und MN bis zum Schnittpunkt im Punkt K fort. Der Punkt K liegt auf der Linie BC, was bedeutet, dass er zur Ebene (ABC) gehört, sodass wir eine Linie durch ihn und den in dieser Ebene liegenden Punkt E ziehen können. Es schneidet die Kante CD im Punkt H. EH ist seine Spur (unsichtbar). Da H und N in derselben Ebene (CDD1) liegen, kann eine Gerade durch sie gezogen werden. Wir erhalten die Spur HN (unsichtbar).

Die Ebenen (ABC) und (A1B1C1) sind parallel. Einer davon enthält die Gerade EH, der andere den Punkt M. Wir können eine Gerade durch M parallel zu EH zeichnen. Wir erhalten die Spur MF (sichtbar). Wir zeichnen eine Gerade durch die Punkte M und F.

Das Sechseck MNHEPF ist der erforderliche Abschnitt.

Wenn wir die Linie MN bis zum Schnittpunkt mit einer anderen Linie in der Ebene (BCC1) mit BB1 fortsetzen würden, dann würden wir einen Punkt G erhalten, der zur Ebene (ABB1) gehört. Das bedeutet, dass man durch G und P eine Gerade zeichnen kann, deren Spur PF ist. Weiter ziehen wir gerade Linien durch Punkte, die in parallelen Ebenen liegen, und kommen zum gleichen Ergebnis.

Wenn man mit der Geraden PE arbeitet, erhält man den gleichen Querschnitt MNHEPF.

4) Konstruieren Sie einen Abschnitt des Würfels durch eine Ebene, die durch die Punkte M, N, P verläuft.

Hier können wir eine Gerade durch die Punkte M und N zeichnen, die in derselben Ebene liegen (A1B1C1). Ihr Fußabdruck ist MN (sichtbar). Es gibt keine Punkte mehr, die in derselben Ebene oder in parallelen Ebenen liegen.

Wir setzen die Linie MN fort. Sie liegt in der Ebene (A1B1C1), kann also nur eine der Geraden in dieser Ebene schneiden. Es gibt bereits Schnittpunkte mit A1D1 und C1D1 - N und M. Zwei weitere Linien dieser Ebene sind A1B1 und B1C1. Der Schnittpunkt von A1B1 und MN ist S. Da er auf der Geraden A1B1 liegt, gehört er zur Ebene (ABB1), was bedeutet, dass eine Gerade durch ihn und den Punkt P gezogen werden kann, der in derselben Ebene liegt. Die Linie PS schneidet die Kante AA1 im Punkt E. PE ist ihre Spur (sichtbar). Durch die Punkte N und E, die in derselben Ebene liegen (ADD1), ist es möglich, eine gerade Linie zu zeichnen, deren Spur NE (unsichtbar) ist. Es gibt eine Linie NE in der Ebene (ADD1) und einen Punkt P in der Ebene parallel dazu (BCC1). Durch den Punkt P können wir eine Linie PL parallel zu NE zeichnen. Sie schneidet die Kante CC1 im Punkt L. PL ist die Spur dieser Linie (sichtbar). Die Punkte M und L liegen in derselben Ebene (CDD1), was bedeutet, dass eine Gerade durch sie gezogen werden kann. Ihr Fußabdruck ist ML (unsichtbar). Das Fünfeck MLPEN ist der erforderliche Abschnitt.

Es war möglich, die Linie NM in beide Richtungen fortzusetzen und ihre Schnittpunkte nicht nur mit der Linie A1B1, sondern auch mit der Linie B1C1 zu suchen, die ebenfalls in der Ebene (A1B1C1) liegt. In diesem Fall zeichnen wir zwei Geraden gleichzeitig durch den Punkt P: eine in der Ebene (ABB1) durch die Punkte P und S und die zweite in der Ebene (BCC1) durch die Punkte P und R. Danach , es bleibt übrig, die in derselben Ebene liegenden Punkte zu verbinden: M c L, E - mit N.