casa › Motore › Costruzione di sezioni di poliedri. Lavoro di ricerca sul tema "Metodi per costruire sezioni di poliedri"

Costruzione di sezioni di poliedri. Lavoro di ricerca sul tema "Metodi per costruire sezioni di poliedri"

L'attività stessa di solito va così: "costruisci una vista naturale della figura della sezione". Naturalmente, abbiamo deciso di non lasciare da parte questa domanda e provare, se possibile, a spiegare come è costruita la sezione obliqua.

Per spiegare come si costruisce una sezione obliqua, farò alcuni esempi. Ovviamente inizierò con l'elementare, aumentando gradualmente la complessità degli esempi. Spero che dopo aver analizzato questi esempi di disegni in sezione, capirai come farlo e sarai in grado di completare da solo il tuo compito di apprendimento.

Considera un "mattone" con dimensioni di 40x60x80 mm da un piano inclinato arbitrario. Il piano di taglio lo taglia lungo i punti 1-2-3-4. Penso che qui sia tutto chiaro.

Passiamo alla costruzione di una forma naturale della figura in sezione.
1. Prima di tutto, disegniamo l'asse della sezione. L'asse dovrebbe essere disegnato parallelamente al piano di sezione - parallelo alla linea in cui il piano è proiettato nella vista principale - di solito è nella vista principale che l'attività è impostata per costruzione di una sezione obliqua(Più avanti menzionerò sempre la vista principale, tenendo presente che questo è quasi sempre il caso dei disegni didattici).
2. Sull'asse, mettiamo da parte la lunghezza della sezione. Nel mio disegno, è designato come L. La dimensione L è determinata nella vista principale ed è uguale alla distanza dal punto in cui la sezione entra nella parte al punto in cui esce.
3. Dai due punti risultanti sull'asse perpendicolare ad esso, mettiamo da parte le larghezze della sezione in questi punti. La larghezza della sezione nel punto di entrata nel pezzo e nel punto di uscita dal pezzo può essere determinata nella vista dall'alto. IN questo caso entrambi i segmenti 1-4 e 2-3 sono pari a 60 mm. Come puoi vedere dall'immagine sopra, i bordi della sezione sono diritti, quindi colleghiamo semplicemente i nostri due segmenti risultanti, ottenendo un rettangolo 1-2-3-4. Questa è la vista naturale della figura della sezione del nostro mattone con un piano inclinato.

Ora complichiamo i nostri dettagli. Mettiamo un mattone sulla base 120x80x20 mm e aggiungiamo rinforzi alla figura. Disegniamo un piano di taglio in modo che passi attraverso tutti e quattro gli elementi della figura (attraverso la base, il mattone e due rinforzi). Nell'immagine qui sotto puoi vedere tre viste e un'immagine realistica di questa parte.

Proviamo a costruire una visione naturale di questa sezione inclinata. Ricominciamo con l'asse di sezione: disegnatelo parallelamente al piano di sezione indicato nella vista principale. Su di esso mettiamo da parte la lunghezza della sezione uguale ad A-E. Il punto A è il punto di ingresso della sezione nella parte e, in un caso particolare, il punto di ingresso della sezione nella base. Il punto di uscita dalla base è il punto B. Segniamo il punto B sull'asse della sezione. Allo stesso modo, contrassegniamo i punti di entrata-uscita al bordo, al "mattone" e al secondo bordo. Dai punti A e B perpendicolari all'asse, mettiamo da parte segmenti pari alla larghezza della base (su ciascun lato dell'asse, 40, solo 80 mm). Collegare punti estremi- otteniamo un rettangolo, che è una vista naturale della sezione della base del pezzo.

Ora è il momento di costruire un pezzo di sezione, che è una sezione del bordo della parte. Dai punti B e C, mettiamo da parte perpendicolari di 5 mm in ciascuna direzione: otterremo segmenti di 10 mm. Collega i punti estremi e ottieni la sezione trasversale della nervatura.

Dai punti C e D mettiamo da parte segmenti perpendicolari pari alla larghezza del "mattone" - del tutto simile al primo esempio di questa lezione.

Tralasciate le perpendicolari dai punti D ed E pari alla larghezza del secondo spigolo e congiungendo i punti estremi, si ottiene una visione naturale della sua sezione.

Resta da cancellare i ponticelli tra i singoli elementi della sezione risultante e applicare il tratteggio. Dovresti ottenere qualcosa del genere:

Se, secondo una data sezione, dividiamo la figura, allora vedremo la seguente vista:

Spero che tu non sia intimidito dai noiosi paragrafi della descrizione dell'algoritmo. Se hai letto tutto quanto sopra e ancora non hai compreso appieno, come disegnare una sezione trasversale, Ti consiglio vivamente di prendere un pezzo di carta e una matita tra le mani e provare a ripetere tutti i passaggi dopo di me: questo ti aiuterà quasi al 100% a imparare il materiale.

Una volta ho promesso la continuazione di questo articolo. Infine, sono pronto a presentarti una costruzione passo-passo di una sezione obliqua di una parte, più vicina al livello dei compiti. Inoltre, la sezione obliqua è definita nella terza vista (la sezione obliqua è definita nella vista di sinistra)

O annota il nostro numero di telefono e parla di noi ai tuoi amici: probabilmente qualcuno sta cercando un modo per fare dei disegni

O crea una nota sulle nostre lezioni sulla tua pagina o sul tuo blog e qualcun altro sarà in grado di padroneggiare il disegno.

Sì, va tutto bene, ma vorrei vedere come si fa la stessa cosa su una parte più complessa, con smussi e foro conico, per esempio.

Grazie. Ma i rinforzi non sono tratteggiati sui tagli?
Esattamente. Sono loro che non si schiudono. Perchè loro sono regole generali facendo dei tagli. Tuttavia, di solito vengono tratteggiate quando si eseguono tagli nelle proiezioni assonometriche: isometria, dimetria, ecc. Quando si eseguono sezioni inclinate, viene ombreggiata anche l'area relativa all'irrigidimento.

Grazie, molto accessibile. Puoi dirmi se la sezione obliqua può essere eseguita nella vista dall'alto o nella vista da sinistra? In tal caso, mi piacerebbe vedere l'esempio più semplice. Per favore.

È possibile effettuare tali tagli. Ma sfortunatamente non ho un esempio a portata di mano in questo momento. E ce n'è un altro punto interessante: da un lato non c'è niente di nuovo lì, ma dall'altro, in pratica, è davvero più difficile disegnare tali sezioni. Per qualche ragione, tutto inizia a confondersi nella testa e la maggior parte degli studenti ha difficoltà. Ma non mollare!

Sì, va tutto bene, ma vorrei vedere come si fa la stessa cosa, ma con i buchi (passanti e non passanti), altrimenti non si trasformano mai in un'ellisse nella mia testa

aiutatemi con un problema complesso

È un peccato che tu abbia scritto qui. Scrivevamo per posta - forse avremmo tempo per discutere di tutto.

Spiega bene. Cosa succede se uno dei lati della parte è semicircolare? Inoltre, ci sono dei buchi nella parte.

Ilya, usa la lezione dalla sezione sulla geometria descrittiva "Sezione di un cilindro da un piano inclinato". Con esso puoi capire cosa fare con i fori (sono anche cilindri infatti) e con un lato semicircolare.

Ringrazio l'autore per l'articolo!Breve e comprensibile.Circa 20 anni fa io stesso rosicchiavo il granito della scienza, ora aiuto mio figlio. Ho dimenticato molto, ma il tuo articolo ha restituito una comprensione fondamentale dell'argomento. Andrò con la sezione inclinata del cilindro da affrontare)

Aggiungi il tuo commento.

Assiomi della planimetria:

In vari libri di testo, le proprietà delle linee e dei piani possono essere presentate in modi diversi, sotto forma di un assioma, una sua conseguenza, un teorema, un lemma, ecc. Considera il libro di testo Pogorelov A.V.

La retta divide il piano in due semipiani.

Da qualsiasi semiretta a un dato semipiano, si può deporre un angolo con un dato misura di grado, inferiore a 180 0 , e uno solo.

Qualunque sia il triangolo, esiste un triangolo uguale in una data posizione rispetto alla data semiretta.

Per un punto non giacente su una retta data si può tracciare al massimo una retta nel piano parallelo alla retta data.

Assiomi della stereometria:

Qualunque sia il piano, ci sono punti che appartengono a questo piano, punti che non appartengono a questo piano e punti che non gli appartengono.

Se due piani diversi hanno un punto in comune, allora si intersecano lungo una retta passante per questo punto.

Se due linee diverse hanno un punto in comune, è possibile tracciare un piano attraverso di esse e, inoltre, solo uno.

Qualunque sia la linea, ci sono punti che appartengono a questa linea e punti che non le appartengono.

Attraverso due punti qualsiasi puoi tracciare una linea e solo una.

Dei tre punti su una linea, uno e solo uno si trova tra gli altri due.

Ogni segmento ha una certa lunghezza maggiore di zero. La lunghezza di un segmento è uguale alla somma delle lunghezze delle parti in cui è diviso per uno qualsiasi dei suoi punti.

Una retta appartenente ad un piano divide questo piano in due semipiani.

Ogni angolo ha una certa misura di grado maggiore di zero. L'angolo piatto è 180 0 . La misura in gradi di un angolo è uguale alla somma dei gradi misura degli angoli in cui è diviso da qualsiasi raggio passante tra i suoi lati.

Su qualsiasi semiretta dal suo punto di partenza, puoi rimandare un segmento di una data lunghezza, e solo uno.

Da una semiretta sul piano che la contiene, un angolo con una data misura in gradi inferiore a 180 può essere tracciato in un dato semipiano 0 , e uno solo.

Qualunque sia il triangolo, c'è un triangolo uguale nel piano dato in una data posizione rispetto alla data semiretta in quel piano.

In un piano, per un punto dato non giacente su una retta data, si può tracciare al massimo una retta parallela alla retta data.

sezione trasversale

Nello spazio due figure, nel nostro caso un piano e un poliedro possono avere la seguente disposizione reciproca: non si intersecano, si intersecano in un punto, si intersecano in linea retta e il piano interseca il poliedro lungo il suo interno (Fig. 1) , e allo stesso tempo formare le seguenti figure:

a) una figura vuota (non intersecare)

b) punto

c) tagliare

d) poligono

Se c'è un poligono all'intersezione di un poliedro e un piano, allora questo poligonosi chiama sezione di un poliedro con un piano .

Fig. 1

Definizione. sezione trasversale un corpo spaziale (ad esempio un poliedro) è una figura ottenuta all'intersezione di un corpo con un piano.

piano di taglio poliedro Chiamiamo qualsiasi piano, su entrambi i lati del quale ci sono punti di un dato poliedro.

Considereremo solo il caso in cui il piano interseca il poliedro lungo il suo interno. In questo caso, l'intersezione di questo piano con ciascuna faccia del poliedro sarà un certo segmento.

Se i piani si intersecano in una linea retta, viene chiamata la linea rettada uno di questi piani all'altro.

Nel caso generale, il piano secante di un poliedro interseca il piano di ciascuna delle sue facce (così come qualsiasi altro piano secante di questo poliedro). Inoltre interseca ciascuna delle linee su cui giacciono i bordi del poliedro.

Viene chiamata la linea lungo la quale il piano secante interseca il piano di qualsiasi faccia del poliedroseguendo il piano di taglio sul piano di questa faccia, e si chiama il punto in cui il piano secante interseca la linea contenente qualsiasi bordo del poliedroseguendo il piano di taglio SUquesta linea retta. Questo punto è anche la traccia di una retta sul piano di taglio. Se il piano di taglio interseca direttamente la faccia del poliedro, allora possiamo parlare della traccia del piano di taglio sulla faccia, e, analogamente, ditraccia di un piano di taglio su un bordo di un poliedro, cioè la traccia di un bordo su un piano di taglio.

Poiché una retta è univocamente determinata da due punti, per trovare la traccia di un piano secante su qualunque altro piano e, in particolare, sul piano di qualunque faccia di un poliedro, basta costruire due punti comuni dei piani

Per costruire una traccia di un piano secante, così come per costruire una sezione di un poliedro da questo piano, è necessario specificare non solo il poliedro, ma anche il piano secante. E la costruzione del piano di sezione avviene in base all'assegnazione di questo piano. I modi principali per definire un piano, e in particolare un piano secante, sono i seguenti:

tre punti non giacenti su una linea retta;

una linea retta e un punto che non giace su di essa;

due linee parallele;

due linee che si intersecano;

un punto e due linee che si intersecano;

Esistono altri modi per definire il piano di taglio.

Pertanto, tutti i metodi per costruire sezioni di poliedri possono essere suddivisi in metodi.

Metodi per la costruzione di sezioni di poliedri

Il metodo delle sezioni di poliedri in stereometria viene utilizzato nei problemi di costruzione. Si basa sulla capacità di costruire una sezione di un poliedro e determinare il tipo di sezione.

Esistono tre metodi principali per costruire sezioni di poliedri:

Metodo assiomatico:

metodo della traccia.

Metodo combinato.

metodo delle coordinate.

Nota che il metodo delle tracce e il metodo delle sezioni ausiliarie sono varietàMetodo assiomatico per la costruzione di sezioni.

Possiamo anche distinguere i seguenti metodi per costruire sezioni di poliedri:

costruzione di una sezione di un poliedro da un piano passante per un dato punto parallelo ad un dato piano;

costruzione di una sezione passante per una data retta parallela ad un'altra data retta;

costruzione di una sezione passante per un dato punto parallela a due date rette oblique;

costruzione di una sezione di un poliedro per un piano passante per una data retta perpendicolare ad un dato piano;

costruzione di una sezione di un poliedro per un piano passante per un dato punto perpendicolare ad una data retta.

Le azioni principali che costituiscono i metodi per costruire sezioni sono trovare il punto di intersezione di una retta con un piano, costruire una linea di intersezione di due piani, costruire una retta parallela a un piano perpendicolare al piano. Per costruire una linea retta di intersezione di due piani, di solito si trovano due dei suoi punti e si traccia una linea retta attraverso di essi. Per costruire il punto di intersezione di una retta e di un piano, trova una retta nel piano che interseca quella data. Quindi il punto desiderato si ottiene all'intersezione della linea trovata con quella data.

Considera separatamente elencato da noimetodi per costruire sezioni di poliedri:

metodo della traccia.

metodo della traccia si basa (opera) sugli assiomi della stereometria, l'essenza del metodo è costruire una linea ausiliaria, che è l'immagine della linea di intersezione del piano di taglio con il piano di qualsiasi faccia della figura. È più conveniente costruire un'immagine della linea di intersezione del piano di taglio con il piano della base inferiore. Questa lineadetta traccia principale del piano di taglio . Utilizzando la traccia, è facile costruire immagini dei punti del piano di taglio situati sui bordi laterali o sulle facce della figura. Collegando coerentemente le immagini di questi punti, otteniamo l'immagine della sezione desiderata.

Nota che quando si costruisce la traccia principale del piano secante, si usa la seguente affermazione.

Se i punti appartengono al piano secante e non giacciono su una retta, e la loro proiezione (centrale o parallela) sul piano scelto come principale sono, rispettivamente, i punti quindi i punti di intersezione delle linee corrispondenti, cioè i punti e giacciono sulla stessa linea (Fig. 1, a, b).

fig.1.a fig.1.b

Questa linea è la traccia principale del piano di taglio. Poiché i punti giacciono sulla traccia principale, basta trovare due di questi tre punti per costruirla.

Metodo delle sezioni ausiliarie.

Questo metodo di costruzione di sezioni di poliedri è sufficientemente universale. Nei casi in cui la traccia (o le tracce) desiderata del piano di taglio è esterna al disegno, questo metodo presenta anche alcuni vantaggi. Allo stesso tempo, va tenuto presente che le costruzioni eseguite con questo metodo risultano spesso "affollate". Tuttavia, in alcuni casi il metodo delle sezioni ausiliarie risulta essere il più razionale.

Metodo combinato

L'essenza del metodo combinato per costruire sezioni di poliedri è l'applicazione di teoremi sul parallelismo di linee e piani nello spazio in combinazione con il metodo assiomatico.

Metodo delle coordinate per la costruzione di sezioni.

L'essenza del metodo delle coordinate è calcolare le coordinate dei punti di intersezione dei bordi o un poliedro con un piano secante, che è dato dall'equazione del piano. L'equazione del piano di sezione viene calcolata in base alle condizioni del problema.

Nota che questo metodo di costruzione di una sezione di un poliedro è accettabile per un computer, poiché è associato a una grande quantità di calcoli e quindi è consigliabile implementare questo metodo utilizzando un computer.

Il nostro compito principale sarà costruire una sezione di un poliedro con un piano, ad es. nella costruzione dell'intersezione di questi due insiemi.

Costruzione di sezioni di poliedri

Notiamo anzitutto che la sezione di un poliedro convesso è un poligono piano convesso, i cui vertici nel caso generale sono i punti di intersezione del piano secante con i bordi del poliedro, ed i lati con le sue facce.

Esempi di creazione di sezioni:

Esistono molti modi diversi per definire una sezione. Il più comune di questi è il metodo di specificare un piano di taglio da tre punti che non giacciono su una linea retta.

Esempio 1 Per scatola ABCDA 1 B 1 C 1 D 1 . Costruire una sezione passante per i punti M, N, L.

Soluzione:

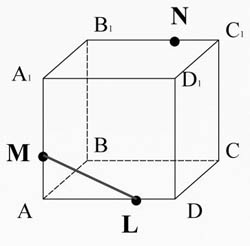
Collega i punti M e L che giacciono nel piano AA 1 D 1 D.

Intersecare la linea ML (appartenente alla sezione) con lo spigolo A 1 D 1 1 D 1 D. Prendi il punto X 1 .

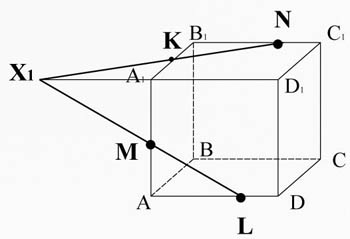
Il punto X1 giace sul bordo A 1 D 1 , e quindi i piani A 1 B 1 C 1 D 1 , collegalo con un punto N giacente sullo stesso piano.

X 1 N interseca il bordo A 1 B 1 al punto k.

Collega i punti K e M che giacciono sullo stesso piano AA 1 B 1 B.

Trova la linea di intersezione del piano di sezione con il piano DD 1 C 1 C:

Intersecare la linea ML (appartenente alla sezione) con lo spigolo DD 1 , giacciono sullo stesso piano AA 1 D 1 D, trova il punto X 2 .

Intersechiamo la linea KN (appartenente alla sezione) con lo spigolo D 1 C 1 , giacciono sullo stesso piano A 1 B 1 C 1 D 1 , otteniamo il punto X3;

I punti X2 e X3 giacciono nel piano DD 1 C 1 C. Disegna una linea X 2 X 3 , che interseca il bordo C 1 C nel punto T e il bordo DC nel punto P. E colleghiamo i punti L e P, che giacciono nel piano ABCD.

Pertanto, il problema è considerato risolto se vengono trovati tutti i segmenti lungo i quali il piano interseca le facce del poliedro, cosa che abbiamo fatto. MKNTPL - sezione desiderata.

Nota. Lo stesso compito per la costruzione di una sezione può essere risolto utilizzando la proprietà dei piani paralleli.

Da quanto sopra, possiamo comporre un algoritmo (regola) per risolvere problemi di questo tipo.

Regole per la costruzione di sezioni di poliedri:

Esempio 2 Dl, M

Risolviamo con il metodo assiomatico:

Disegna un piano ausiliarioDKM, che interseca gli spigoli AB e BC nei punti E eF(il corso della soluzione è in Fig. 2.). Costruiamo una "traccia" del CM del piano di sezione su questo piano ausiliario, troviamo il punto di intersezione di CM ed EF- punto P. Punto P, così comel, giace nel piano ABC, ed è possibile tracciare una retta lungo la quale il piano di sezione interseca il piano ABC ("traccia" della sezione nel piano ABC).

Esempio 3 Sugli spigoli AB e AD della piramide MABCD, fissiamo i punti P e Q, rispettivamente, i punti medi di questi spigoli, e sullo spigolo MC, fissiamo il punto R. Costruiamo una sezione della piramide per un piano passante per i punti P, Q e R.

La soluzione sarà effettuata con un metodo combinato:

1). È chiaro che la traccia principale del piano PQR è la linea PQ.

2). Trova il punto K in cui il piano MAC interseca la linea PQ. I punti K e R appartengono sia al piano PQR che al piano MAC. Pertanto, tracciando la linea retta KR, otteniamo la linea di intersezione di questi piani.

3). Troviamo il punto N=AC BD, tracciamo la retta MN e troviamo il punto F=KR MN.

4). Il punto F è punto comune piani PQR e MDB, cioè questi piani si intersecano lungo una retta passante per il punto F. Allo stesso tempo, poiché PQ è la linea mediana del triangolo ABD, allora PQ è parallela a BD, cioè anche la linea PQ è parallela al piano MDB. Allora il piano PQR passante per la retta PQ interseca il piano MDB lungo la retta parallela alla retta PQ, cioè parallela alla retta BD. Quindi nel piano MDB per il punto F tracciamo una retta parallela alla retta BD.

5). Ulteriori costruzioni sono chiare dalla figura. Di conseguenza, otteniamo il poligono PQD"RB" - la sezione richiesta

Considera le sezioni del prisma per semplicità, cioè per comodità del pensiero logico, si considerino le sezioni del cubo (Fig. 3.a):

Riso. 3.a

Le sezioni del prisma per piani paralleli ai bordi laterali sono parallelogrammi. In particolare, le sezioni diagonali sono parallelogrammi (Fig. 4).

def. sezione diagonale un prisma è una sezione di un piano passante per due spigoli laterali che non appartengono alla stessa faccia.

Il poligono risultante da una sezione diagonale di un prisma è un parallelogramma. Domanda sul numero di sezioni diagonaliN-il prisma angolare è più difficile della questione del numero di diagonali. Ci saranno tante sezioni quante sono le diagonali alla base. Sappiamo che un prisma convesso ha alla base poligoni convessi, mentre uno convessoN-gon di diagonali. E quindi possiamo dire che ci sono la metà delle sezioni diagonali quante sono le diagonali.

Nota: Quando si costruiscono sezioni di un parallelepipedo nella figura, si dovrebbe tener conto del fatto che se il piano di taglio interseca due facce opposte lungo alcuni segmenti, allora questi segmenti sono paralleli “per la proprietà del parallelepipedo, cioè Le facce opposte di un parallelepipedo sono parallele e uguali.

Forniamo risposte alle domande più frequenti:

Quali poligoni si ottengono nella sezione di un cubo da un piano?

"triangolo, quadrilatero, pentagono, esagono".

Può una sezione trasversale piana di un cubo produrre un ettagono? E l'ottagono?

"non può".

3) Sorge la domanda, qual è il maggior numero di lati di un poligono ottenuto da una sezione di un poliedro con un piano?

Numero più grande lati del poligono ottenuti nella sezione del poliedro dal piano è uguale al numero di facce del poliedro .

Esempio 3 Costruisci una sezione del prisma A 1 B 1 C 1 D 1 ABCD da un piano passante per tre punti M, N, K.

Si consideri il caso della localizzazione dei punti M, N, K sulla superficie di un prisma (Fig. 5).

Consideriamo il caso: In questo caso è ovvio che M1 = B1.

Edificio:

Esempio 4 Costruisci una sezione del parallelepipedo ABCDA 1 B 1 C 1 D 1 un piano passante per i punti M, N, P (i punti sono indicati nel disegno (Fig. 6)).

Soluzione:

Riso. 6

I punti N e P giacciono nel piano della sezione e nel piano della base inferiore del parallelepipedo. Costruiamo una retta passante per questi punti. Questa retta è la traccia del piano secante sul piano di base del parallelepipedo.

Continuiamo la linea su cui giace il lato AB del parallelepipedo. Le rette AB e NP si intersecano in un punto S. Questo punto appartiene al piano di sezione.

Poiché anche il punto M appartiene al piano di sezione e interseca la retta AA 1 ad un certo punto x.

I punti X e N giacciono sullo stesso piano della faccia AA 1 D 1 D, collegali e ottieni la linea XN.

Poiché i piani delle facce del parallelepipedo sono paralleli, è possibile tracciare una retta per il punto M nella faccia A 1 B 1 C 1 D 1 parallela alla retta NP. Questa linea intersecherà il lato B 1 CON 1 al punto Y.

Allo stesso modo, tracciamo la linea YZ, parallela alla linea XN. Colleghiamo Z con P e otteniamo la sezione desiderata - MYZPNX.

Le sezioni della piramide per piani che passano attraverso la sua sommità sono triangoli. In particolare, le sezioni diagonali sono triangoli. Si tratta di sezioni per piani passanti per due spigoli laterali non adiacenti della piramide.

Esempio 4 Costruisci una sezione della piramide ABCDun piano passante per i punti K,l, M.

Soluzione:

Risolviamo lo stesso esempio in modo diverso. .

Supponiamo che per i punti K,l, e Ì la sezioneKLMN(figura 7). Denotare conFil punto di intersezione delle diagonali del quadrilateroKLMN. Disegniamo una linea rettaDFe denotare conF 1 il suo punto di intersezione con la faccia ABC. PuntoF 1 coincide con il punto di intersezione delle rette AM e SK (F 1 appartiene contemporaneamente ai piani AMDEDSC). puntoF 1 facile da costruire. Quindi costruiamo un puntoFcome punto di intersezioneDF 1 EL.M. Poi troviamo il puntoN.

Il metodo considerato è chiamatometodo di progettazione interna . (Per il nostro caso noi stiamo parlando sul design centrale. quadrilateroKISA è la proiezione di un quadrilateroKMNLda un puntoD. In questo caso, il punto di intersezione delle diagonaliKMNL- puntoF- va al punto di intersezione delle diagonali del quadrilateroKISA - puntoF 1 .

Area sezionale di un poliedro.

Il problema del calcolo dell'area della sezione trasversale di un poliedro viene solitamente risolto in più fasi. Se il problema dice che la sezione è costruita (o che il piano di taglio è disegnato, ecc.), allora nella prima fase della soluzione si scopre la forma della figura ottenuta nella sezione.

Questo deve essere fatto per selezionare la formula appropriata per il calcolo dell'area della sezione trasversale. Dopo aver chiarito la forma della figura ottenuta nella sezione e scelto la formula per calcolare l'area di questa figura, si procede direttamente al lavoro computazionale.

In alcuni casi può risultare più semplice se, senza conoscere la forma della figura ottenuta nella sezione, si proceda subito a calcolarne l'area utilizzando la formula che segue dal teorema.

Il teorema sull'area della proiezione ortogonale di un poligono: l'area della proiezione ortogonale di un poligono su un piano è uguale al prodotto della sua area e al coseno dell'angolo tra il piano del poligono e il piano di proiezione: .

Una formula valida per il calcolo dell'area della sezione trasversale è: dove è l'area della proiezione ortogonale della figura ottenuta nella sezione, ed è l'angolo tra il piano secante e il piano su cui è proiettata la figura. Con tale soluzione è necessario costruire una proiezione ortogonale della figura ottenuta nella sezione e calcolare

Se la condizione del problema dice che la sezione deve essere costruita e deve essere trovata l'area della sezione ottenuta, allora nella prima fase è ragionevole costruire la sezione data e quindi, naturalmente, determinare la forma di la cifra ottenuta nella sezione, ecc.

Notiamo il seguente fatto: poiché si costruiscono sezioni di poliedri convessi, anche il poligono di sezione sarà convesso, quindi la sua area può essere trovata dividendolo in triangoli, cioè l'area della sezione è uguale alla somma delle aree del triangoli da cui è composto.

Compito 1.

– corretto piramide triangolare con un lato di base uguale e uguale ad un'altezza Costruisci una sezione della piramide da un piano passante per i punti, dove è il punto medio del lato, e trova la sua area (Fig. 8).

Soluzione.

La sezione trasversale della piramide è un triangolo. Troviamo la sua area.

Poiché la base della piramide è un triangolo equilatero e il punto è il punto medio del lato, allora è l'altezza e poi, .

L'area di un triangolo può essere trovata:

Compito 2.

Costola laterale di un prisma regolare è uguale al lato della base. Costruisci sezioni di un prisma per piani passanti per un puntoUN, perpendicolare alla linea Se trovi l'area della sezione risultante del prisma.

Soluzione.

Costruiamo la sezione data. Facciamolo da considerazioni puramente geometriche, per esempio, come segue.

In un piano passante per una data linea e un dato punto, tracciamo una linea attraverso questo punto perpendicolare alla linea (Fig. 9). Usiamo a questo scopo il fatto che nel triangolo cioè, la sua mediana è anche l'altezza di questo triangolo. Quindi, una linea retta.

Attraverso il punto tracciamo un'altra linea perpendicolare alla linea. Disegniamolo, ad esempio, in un piano passante per una retta. È chiaro che questa linea è una linea

Quindi, vengono costruite due linee intersecanti, perpendicolari alla linea. Queste linee definiscono un piano passante per un punto perpendicolare alla linea, cioè viene dato un piano secante.

Costruiamo una sezione del prisma da questo piano. Si noti che poiché la linea è parallela al piano. Quindi il piano che passa per la linea interseca il piano lungo una linea parallela alla linea, cioè la linea. Disegna una linea retta attraverso il punto e collega il punto risultante con un punto.

Sezione quadrilatera data. Determiniamo la sua area.

È chiaro che un quadrilatero è un rettangolo, cioè la sua area

riso. 9

COSTRUZIONE DI SEZIONI E SEZIONI SU DISEGNO

Il disegno della parte è formato aggiungendo in sequenza le sporgenze, i tagli e le sezioni necessarie. Inizialmente, viene creata una vista personalizzata con un modello specificato dall'utente e l'orientamento del modello è impostato per adattarsi al meglio alla vista principale. Inoltre, vengono creati i tagli e le sezioni necessarie per questo e per i seguenti tipi.

La vista principale (vista frontale) è selezionata in modo tale da dare l'idea più completa delle forme e delle dimensioni della parte.

Sezioni nei disegni

A seconda della posizione del piano di taglio si distinguono le seguenti tipologie di taglio:

A) orizzontale, se il piano di taglio è parallelo al piano di proiezione orizzontale;

B) verticale, se il piano di taglio è perpendicolare al piano di proiezione orizzontale;

C) inclinato - il piano di taglio è inclinato rispetto ai piani di proiezione.

Le sezioni verticali sono suddivise in:

· frontale: il piano di taglio è parallelo al piano di proiezione frontale;

· profilo - il piano di taglio è parallelo al piano di proiezione del profilo.
A seconda del numero di piani di taglio, i tagli sono:

· semplice - con un piano di taglio (Fig. 107);

· complesso - con due o più piani di taglio (Fig. 108)
Lo standard prevede i seguenti tipi di tagli complessi:

· a gradini, quando i piani secanti sono paralleli (Fig. 108 a) e le linee tratteggiate - i piani secanti si intersecano (Fig. 108 b)

Fig.107 Taglio semplice

A)b)

Fig.108 Tagli complessi

Designazione dei tagli

Nel caso in cui in una sezione semplice il piano secante coincida con il piano di simmetria dell'oggetto, la sezione non è indicata (Fig. 107). In tutti gli altri casi, le sezioni sono indicate da lettere maiuscole dell'alfabeto russo, che iniziano con la lettera A, ad esempio A-A.

La posizione del piano di taglio nel disegno è indicata dalla linea di sezione - una linea aperta ispessita. Con un taglio complesso si eseguono tratti anche alle inflessioni della linea di sezione. Le frecce che indicano la direzione della vista devono essere posizionate sui tratti iniziale e finale, le frecce devono trovarsi a una distanza di 2-3 mm dalle estremità esterne dei tratti. All'esterno di ciascuna freccia che indica la direzione della vista, è applicata la stessa lettera maiuscola.

Lo stesso pulsante viene utilizzato per designare tagli e sezioni nel sistema KOMPAS Linea di sezione situata nella pagina Legenda (fig.109).

Fig.109 Pulsante linea di sezione

Collegamento di mezza vista a mezza sezione

Se la vista e la sezione sono figure simmetriche (Fig. 110), è possibile collegare metà della vista e metà della sezione, separandole con una linea sottile tratteggiata, che è l'asse di simmetria. Parte della sezione è solitamente posizionata a destra dell'asse di simmetria che separa la parte della vista dalla parte della sezione, oppure al di sotto dell'asse di simmetria. Le curve di livello nascoste sulle parti collegate della vista e della sezione di solito non vengono visualizzate. Se la linea assiale che separa la vista e la sezione coincide con la proiezione di una linea, ad esempio il bordo di una figura sfaccettata, allora la vista e la sezione sono separate da una linea continua ondulata tracciata a sinistra dell'asse di simmetria se il bordo si trova sulla superficie interna, oa destra se il bordo è esterno.

Riso. 110 Collegamento di una parte di una vista e di una sezione

Tagli edilizi

Studieremo la costruzione di sezioni nel sistema KOMPAS usando l'esempio della costruzione di un disegno di un prisma, il cui compito è mostrato in Fig. 111.

La sequenza del disegno è la seguente:

1. Di date dimensioni costruiamo un modello solido di prisma (Fig. 109 b). Salviamo il modello nella memoria del computer in un file chiamato "Prisma".

Fig.112 Pannello Linee

3. Per costruire una sezione del profilo (Fig. 113) disegna una linea sezione A-A nella vista principale utilizzando il pulsante Linea di taglio.

Fig.113 Costruzione di una sezione di profilato

La direzione della vista e il testo della designazione possono essere selezionati sul pannello di controllo con il comando nella parte inferiore dello schermo (Fig. 114). La costruzione della linea di sezione viene completata premendo il pulsante Crea oggetto.

Fig.114 Pannello di controllo per il comando di costruzione di tagli e sezioni

4. Nel pannello Viste associative (Fig. 115), selezionare il pulsante Linea di taglio, quindi specificare la linea di taglio con il sormonto che appare sullo schermo. Se tutto è stato eseguito correttamente (la linea di taglio deve essere tracciata nella vista attiva), la linea di taglio diventerà rossa. Dopo aver specificato la linea di taglio A-A, sullo schermo apparirà un'immagine fantasma sotto forma di un rettangolo complessivo.

Fig.115 Pannello viste associative

Con l'aiuto dell'interruttore Taglio/sezione nella barra delle proprietà, viene selezionato il tipo di immagine - Taglio (Fig. 116) e la scala del taglio visualizzato.

Fig.116 Pannello di controllo per il comando di costruzione di tagli e sezioni

La sezione del profilo verrà costruita automaticamente nella connessione di proiezione e con una notazione standard. Se necessario, la connessione di proiezione può essere disattivata dall'interruttore Attacco sporgente (Fig. 116). Per impostare i parametri di tratteggio che verranno utilizzati nella sezione (sezione) creata, utilizzare i controlli nella scheda Tratteggio.

Fig.117 Costruzione di un tratto orizzontale B-B e di un tratto C-C

Se il piano di taglio selezionato durante la costruzione del taglio coincide con il piano di simmetria della parte, in conformità con lo standard tale taglio non è indicato. Ma se cancelli semplicemente la designazione della sezione, poiché la vista e la sezione nella memoria del computer sono interconnesse, l'intera sezione verrà cancellata. Pertanto, per rimuovere la designazione, è necessario prima distruggere la connessione tra la vista e la sezione. Per fare ciò, fare clic con il pulsante sinistro del mouse per selezionare la sezione, quindi fare clic con il pulsante destro del mouse per aprire il menu contestuale, dal quale è selezionata la voce Distruggi vista (Fig. 97). Ora è possibile eliminare il simbolo della sezione.

5. Per costruire una sezione orizzontale, tracciamo una linea di sezione B-B attraverso il piano inferiore del foro nella vista frontale. La vista frontale deve prima essere resa attuale con due clic del tasto sinistro del mouse. Quindi viene costruita una sezione orizzontale (Fig. 117).

6. Quando si costruisce una sezione frontale, una parte della vista e una parte della sezione sono compatibili, perché sono figure simmetriche. Il bordo esterno del prisma è proiettato sulla linea che separa la vista e il taglio, quindi lo delimitiamo vista e sezione di una solida linea ondulata sottile tracciata a destra dell'asse di simmetria, perché costola esterna. Il pulsante viene utilizzato per disegnare una linea ondulata. Curva di Bezier situata nel pannello Geometria disegnata con lo stile Per linea di ritaglio (Fig. 118). Specificare in sequenza i punti attraverso i quali deve passare la curva di Bezier. Per terminare l'esecuzione del comando, fare clic sul pulsante Crea oggetto.

Fig.118 Selezione di uno stile di linea per un'interruzione

Sezionando

Una sezione è un'immagine di un oggetto ottenuta sezionando mentalmente un oggetto con un piano. La sezione mostra solo ciò che si trova nel piano di taglio.

La posizione del piano di taglio, con cui viene formato il profilato, è indicata nel disegno dalla linea di taglio, esattamente come per i profilati.

Le sezioni, a seconda della loro posizione nei disegni, sono suddivise in estese e sovrapposte. Le sezioni rimosse si trovano più spesso sul campo libero del disegno e sono delineate dalla linea principale. Le sezioni sovrapposte sono poste direttamente sull'immagine dell'oggetto e delineate con linee sottili (Fig. 119).

Fig.119 Costruzione di sezioni

Considera la sequenza di costruzione di un disegno di un prisma con un obliquo esteso sezione B-B(figura 117).

1. Attivare la vista frontale facendo doppio clic con il pulsante sinistro del mouse sulla vista e tracciare una linea di sezione utilizzando il pulsante linea di taglio . Selezioniamo il testo dell'iscrizione В-В.

2. Utilizzando il pulsante Taglia linea situato nel pannello Viste associative (Fig. 115), che appare come una trappola, indicare la linea secante aerei B-B. Utilizzando l'interruttore Taglia/sezione sulla barra delle proprietà, selezionare il tipo di immagine - Sezione (Fig. 116), la scala della sezione visualizzata viene selezionata dalla finestra Scala.

La sezione costruita si trova in una relazione di proiezione, che ne limita il movimento nel disegno, ma la relazione di proiezione può essere disattivata utilizzando il pulsante connessione di proiezione.

Sul disegno finito, disegna linee centrali, se necessario, inserire le dimensioni.

I compiti per la costruzione di sezioni di poliedri prendono luogo significativo come corso di geometria scolastica per le scuole superiori, e agli esami di vari livelli. La soluzione di questo tipo di problemi contribuisce all'assimilazione degli assiomi della stereometria, alla sistematizzazione delle conoscenze e delle abilità, allo sviluppo rappresentazione spaziale e abilità costruttive. Sono ben note le difficoltà che si presentano nel risolvere problemi sulla costruzione di profilati.

Dal prima infanzia siamo di fronte a tagli. Tagliamo pane, salsiccia e altri prodotti, tagliamo un bastoncino o una matita con un coltello. Il piano secante in tutti questi casi è il piano del coltello. Le sezioni (sezioni di pezzi) sono diverse.

La sezione di un poliedro convesso è un poligono convesso, i cui vertici, nel caso generale, sono i punti di intersezione del piano di taglio con i bordi del poligono, ei lati sono le linee di intersezione del piano di taglio con le facce.

Per costruire una linea di intersezione di due piani, è sufficiente trovare due punti comuni di questi piani e tracciare una linea attraverso di essi. Questo si basa sulle seguenti affermazioni:

1. se due punti di una retta appartengono a un piano, allora tutta la retta appartiene a questo piano;

2. se due piani diversi hanno un punto in comune, allora si intersecano lungo una retta passante per questo punto.

Come ho già detto, la costruzione di sezioni di poliedri può essere effettuata sulla base degli assiomi della stereometria e dei teoremi sul parallelismo di rette e piani. Allo stesso tempo, esistono alcuni metodi per costruire sezioni piane di poliedri. I seguenti tre metodi sono i più efficaci:

metodo della traccia

Metodo di progettazione interna

Metodo combinato.

Nello studio della geometria e, in particolare, di quelle sezioni di essa in cui si considerano le immagini forme geometriche, le immagini di forme geometriche aiutano l'uso delle presentazioni al computer. Con l'aiuto di un computer, molte lezioni di geometria diventano più visive e dinamiche. Assiomi, teoremi, dimostrazioni, compiti per la costruzione, compiti per la costruzione di sezioni possono essere accompagnati da costruzioni successive sullo schermo del monitor. I disegni generati dal computer possono essere salvati e incollati in altri documenti.

Voglio mostrare alcune diapositive sull'argomento: "Costruzione di sezioni in corpi geometrici»

Per costruire il punto di intersezione di una retta e di un piano, trova una retta nel piano che interseca la retta data. Quindi il punto desiderato è il punto di intersezione della linea trovata con quella data. Vediamolo nelle prossime slide.

Compito 1.

Due punti M e N sono segnati sui bordi del tetraedro DABC; M GAD, N b DC. Scegli il punto di intersezione della linea MN con il piano della base.

Soluzione: per trovare il punto di intersezione della retta MN con il piano

base continueremo AC e segmento MN. Segnamo il punto di intersezione di queste linee attraverso X. Il punto X appartiene alla linea MN e alla faccia AC, e AC giace nel piano della base, il che significa che anche il punto X giace nel piano della base . Il punto X è quindi il punto di intersezione della retta MN con il piano della base.

Consideriamo il secondo problema. Complichiamolo un po'.

Compito 2.

Dato un tetraedro DABC di punti M e N, dove M € DA, N C (DBC). Trova il punto di intersezione della retta MN con il piano ABC .

Soluzione: Il punto di intersezione della retta MN con il piano ABC deve trovarsi nel piano che contiene la retta MN e nel piano della base. Continuiamo il segmento DN fino al punto di intersezione con il bordo DC. Contrassegniamo il punto di intersezione attraverso E. Continuiamo la linea AE e MN fino al punto della loro intersezione. Nota X. Il punto X appartiene a MN, quindi giace sul piano che contiene la retta MN e X appartiene ad AE, e AE giace sul piano ABC. Quindi anche X giace nel piano ABC. Quindi X è il punto di intersezione della retta MN e del piano ABC.

Complichiamo il compito. Consideriamo una sezione di figure geometriche per piani passanti per tre punti dati.

Compito 3

Sugli spigoli AC, AD e DB del tetraedro DABC sono segnati i punti M, N e P. Costruire una sezione del tetraedro mediante il piano MNP.

Soluzione: costruire una retta lungo la quale il piano MNP. Interseca il piano della faccia ABC. Il punto M è un punto comune di questi piani. Per costruire un altro punto comune, continuiamo il segmento AB e NP. Contrassegniamo il punto di intersezione attraverso X, che sarà il secondo punto comune del piano MNP e ABC. Quindi questi piani si intersecano lungo la retta MX. MX interseca lo spigolo BC in un punto E. Poiché E giace su MX e MX è una retta appartenente al piano MNP, ne consegue che PE appartiene a MNP. Il quadrilatero MNPE è la sezione richiesta.

Compito 4

Costruiamo una sezione di un prisma rettilineo ABCA1B1C1 da un piano passante per i punti P , Q,R, dove R appartiene a ( aa 1C 1C), R appartiene IN 1C1,

Q appartiene ad AB

Soluzione: Tutti e tre punti P,Q,R giacciono in facce diverse, quindi non possiamo ancora costruire una linea di intersezione del piano secante con qualsiasi faccia del prisma. Troviamo il punto di intersezione di PR con ABC. Troviamo le proiezioni dei punti P e R sul piano di base PP1 perpendicolare a BC e RR1 perpendicolare ad AC. La retta P1R1 interseca la retta PR nel punto X. X è il punto di intersezione della retta PR con il piano ABC. Giace nel piano desiderato K e nel piano della base, come il punto Q. XQ è una linea retta che interseca K con il piano della base. XQ interseca AC nel punto K. Pertanto, KQ è il segmento dell'intersezione del piano X con la faccia ABC. K e R giacciono nel piano X e nel piano della faccia AA1C1C. Disegna una linea KR e segna il punto di intersezione con A1Q E. KE è la linea di intersezione del piano X con questa faccia. Trova la linea di intersezione del piano X con il piano delle facce BB1A1A. KE interseca A1A nel punto Y. La retta QY è la retta di intersezione del piano secante con il piano AA1B1B. FPEKQ - sezione desiderata.

I compiti per costruire sezioni di un cubo da un piano, di regola, sono più semplici rispetto, ad esempio, ai compiti per sezioni di una piramide.

Possiamo tracciare una retta passante per due punti se giacciono sullo stesso piano. Quando si costruiscono sezioni di un cubo, è possibile un'altra opzione per costruire una traccia di un piano di taglio. Poiché il terzo piano interseca due piani paralleli lungo linee rette parallele, allora se una linea retta è già stata costruita in una delle facce e nell'altra c'è un punto attraverso il quale passa la sezione, allora possiamo tracciare una linea retta attraverso questo punto parallelo a quello dato.

Considera su esempi concreti come costruire sezioni di un cubo da un piano.

1) Costruisci una sezione del cubo da un piano passante per i punti A, C e M.

I problemi di questo tipo sono i più semplici di tutti i problemi per la costruzione di sezioni di un cubo. Poiché i punti A e C giacciono sullo stesso piano (ABC), possiamo tracciare una linea attraverso di essi. La sua traccia è il segmento AC. È invisibile, quindi rappresentiamo AC con un tratto. Allo stesso modo, colleghiamo i punti M e C, che giacciono sullo stesso piano (CDD1), ei punti A e M, che giacciono sullo stesso piano (ADD1). Triangle ACM è la sezione richiesta.

2) Costruire una sezione del cubo mediante un piano passante per i punti M, N, P.

Qui, solo i punti M e N giacciono sullo stesso piano (ADD1), quindi tracciamo una linea retta attraverso di essi e otteniamo la traccia MN (invisibile). Poiché le facce opposte del cubo giacciono su piani paralleli, il piano di taglio interseca i piani paralleli (ADD1) e (BCC1) lungo linee parallele. Abbiamo già costruito una delle linee parallele: questa è MN.

Attraverso il punto P tracciamo una linea parallela a MN. Interseca il bordo BB1 nel punto S. PS è la traccia del piano secante nella faccia (BCC1).

Tracciamo una linea retta attraverso i punti M e S, che giacciono sullo stesso piano (ABB1). Ho la traccia MS (visibile).

I piani (ABB1) e (CDD1) sono paralleli. Esiste già una linea MS nel piano (ABB1), quindi attraverso il punto N nel piano (CDD1) tracciamo una linea parallela a MS. Questa linea interseca il bordo D1C1 nel punto L. La sua traccia è NL (invisibile). I punti P e L giacciono sullo stesso piano (A1B1C1), quindi tracciamo una linea retta attraverso di essi.

Il pentagono MNLPS è la sezione richiesta.

3) Costruire una sezione del cubo mediante un piano passante per i punti M, N, P.

I punti M e N giacciono sullo stesso piano (BCC1), quindi è possibile tracciare una linea retta attraverso di essi. Otteniamo la traccia MN (visibile). Il piano (BCC1) è parallelo al piano (ADD1), quindi attraverso il punto P che giace in (ADD1) tracciamo una linea parallela a MN. Interseca il bordo AD nel punto E. Abbiamo ottenuto la traccia PE (invisibile).

Non ci sono più punti che giacciono sullo stesso piano, o una retta e un punto su piani paralleli. Pertanto, una delle linee già esistenti deve essere proseguita per ottenere un punto aggiuntivo.

Se continuiamo la linea MN, allora, poiché si trova nel piano (BCC1), dobbiamo cercare il punto di intersezione di MN con una delle linee di questo piano. Esistono già punti di intersezione con CC1 e B1C1: questi sono M e N. Le linee BC e BB1 rimangono. Continuiamo BC e MN fino all'intersezione nel punto K. Il punto K si trova sulla linea BC, il che significa che appartiene al piano (ABC), quindi possiamo tracciare una linea attraverso di essa e il punto E che giace su questo piano. Interseca il bordo CD nel punto H. EH è la sua traccia (invisibile). Poiché H e N giacciono sullo stesso piano (CDD1), è possibile tracciare una linea retta attraverso di essi. Otteniamo la traccia HN (invisibile).

I piani (ABC) e (A1B1C1) sono paralleli. Uno di essi contiene la linea EH, l'altro contiene il punto M. Possiamo tracciare una linea attraverso M parallela a EH. Otteniamo la traccia MF (visibile). Tracciamo una linea retta attraverso i punti M e F.

Hexagon MNHEPF è la sezione richiesta.

Se continuassimo la linea MN fino all'intersezione con un'altra linea nel piano (BCC1), con BB1, allora otterremmo un punto G appartenente al piano (ABB1). Ciò significa che attraverso G e P è possibile tracciare una linea la cui traccia è PF. Inoltre, tracciamo linee rette attraverso punti che giacciono su piani paralleli, e arriviamo allo stesso risultato.

Lavorando con la linea retta PE si ottiene la stessa sezione trasversale MNHEPF.

4) Costruire una sezione del cubo per un piano passante per i punti M, N, P.

Qui possiamo tracciare una retta passante per i punti M e N che giacciono sullo stesso piano (A1B1C1). La sua impronta è MN (visibile). Non ci sono più punti che giacciono sullo stesso piano o su piani paralleli.

Continuiamo la linea MN. Si trova nel piano (A1B1C1), quindi può intersecarsi solo con una delle linee in questo piano. Esistono già punti di intersezione con A1D1 e C1D1 - N e M. Altre due linee di questo piano sono A1B1 e B1C1. Il punto di intersezione di A1B1 e MN è S. Poiché si trova sulla linea A1B1, appartiene al piano (ABB1), il che significa che è possibile tracciare una linea attraverso di esso e il punto P, che giace sullo stesso piano. La linea PS interseca lo spigolo AA1 nel punto E. PE ne è la traccia (visibile). Attraverso i punti N ed E, giacenti sullo stesso piano (ADD1), è possibile tracciare una retta, la cui traccia è NE (invisibile). C'è una retta NE nel piano (ADD1), e un punto P nel piano ad essa parallelo (BCC1) Per il punto P possiamo tracciare una retta PL parallela a NE. Interseca lo spigolo CC1 nel punto L. PL è la traccia di questa linea (visibile). I punti M e L giacciono sullo stesso piano (CDD1), il che significa che è possibile tracciare una linea retta attraverso di essi. La sua impronta è ML (invisibile). Il pentagono MLPEN è la sezione richiesta.

Era possibile continuare la linea NM in entrambe le direzioni e cercare i suoi punti di intersezione non solo con la linea A1B1, ma anche con la linea B1C1, anch'essa situata nel piano (A1B1C1). In questo caso, tracciamo due rette attraverso il punto P contemporaneamente: una nel piano (ABB1) attraverso i punti P e S, e la seconda nel piano (BCC1), attraverso i punti P e R. Dopodiché , resta da collegare i punti che giacciono sullo stesso piano: M c L, E - con N.