lar › Motor › Construção de secções de poliedros. Trabalho de investigação subordinado ao tema "Métodos de construção de secções de poliedros"

Construção de secções de poliedros. Trabalho de investigação subordinado ao tema "Métodos de construção de secções de poliedros"

A tarefa em si geralmente é assim: "criar uma visão natural da figura da seção". Claro, decidimos não deixar essa questão de lado e tentar, se possível, explicar como a seção oblíqua é construída.

Para explicar como uma seção oblíqua é construída, darei alguns exemplos. Claro, vou começar com o elementar, aumentando gradativamente a complexidade dos exemplos. Espero que, depois de analisar esses exemplos de desenhos de seção, você entenda como isso é feito e seja capaz de concluir sua tarefa de aprendizado sozinho.

Considere um "tijolo" com dimensões de 40x60x80 mm por um plano inclinado arbitrário. O plano de corte corta ao longo dos pontos 1-2-3-4. Acho que está tudo claro aqui.

Passemos à construção de uma forma natural da figura seccional.
1. Em primeiro lugar, vamos desenhar o eixo da seção. O eixo deve ser traçado paralelo ao plano de corte - paralelo à linha na qual o plano é projetado na vista principal - geralmente é na vista principal que a tarefa é definida para construção de uma seção oblíqua(A seguir, sempre mencionarei a vista principal, lembrando que quase sempre é assim nos desenhos de treinamento).
2. No eixo, reservamos o comprimento da seção. No meu desenho, é designado como L. O tamanho L é determinado na vista principal e é igual à distância do ponto onde o corte entra na peça até o ponto onde sai.
3. Dos dois pontos resultantes no eixo perpendicular a ele, separamos as larguras de seção nesses pontos. A largura da seção no ponto de entrada na peça e no ponto de saída da peça pode ser determinada na vista superior. EM este caso ambos os segmentos 1-4 e 2-3 são iguais a 60 mm. Como você pode ver na figura acima, as bordas da seção são retas, então simplesmente conectamos nossos dois segmentos resultantes, obtendo um retângulo 1-2-3-4. Isto é - a visão natural da figura da seção do nosso tijolo com um plano inclinado.

Agora vamos complicar nosso detalhe. Vamos colocar um tijolo na base de 120x80x20 mm e adicionar reforços à figura. Vamos desenhar um plano de corte para que ele passe por todos os quatro elementos da figura (através da base, tijolo e dois reforços). Na foto abaixo você pode ver três vistas e uma imagem realista desta parte.

Vamos tentar construir uma visão natural desta seção inclinada. Vamos começar novamente com o eixo da seção: desenhe-o paralelo ao plano da seção indicado na vista principal. Nele reservamos o comprimento da seção igual a A-E. O ponto A é o ponto de entrada da seção na peça e, em um caso particular, o ponto de entrada da seção na base. O ponto de saída da base é o ponto B. Vamos marcar o ponto B no eixo da seção. Da mesma forma, marcamos os pontos de entrada-saída para a borda, para o "tijolo" e para a segunda borda. Dos pontos A e B perpendiculares ao eixo, separamos segmentos iguais à largura da base (em cada lado do eixo, 40, apenas 80 mm). Conectar pontos extremos- obtemos um retângulo, que é uma visão natural da seção da base da peça.

Agora é hora de construir um pedaço de seção, que é uma seção da aresta da peça. Dos pontos B e C, separamos perpendiculares de 5 mm em cada direção - obteremos segmentos de 10 mm. Conecte os pontos extremos e obtenha a seção transversal da nervura.

Dos pontos C e D, separamos segmentos perpendiculares iguais à largura do "tijolo" - completamente semelhante ao primeiro exemplo desta lição.

Tendo separado as perpendiculares dos pontos D e E iguais à largura da segunda aresta e conectando os pontos extremos, obtemos uma visão natural de sua seção.

Resta apagar os jumpers entre os elementos individuais da seção resultante e aplicar a hachura. Você deve obter algo como isto:

Se, de acordo com uma determinada seção, dividirmos a figura, veremos a seguinte visualização:

Espero que você não se intimide com os parágrafos tediosos da descrição do algoritmo. Se você leu tudo acima e ainda não entendeu completamente, como desenhar uma seção transversal, Aconselho fortemente que você pegue um pedaço de papel e um lápis nas mãos e tente repetir todos os passos depois de mim - isso vai te ajudar quase 100% a aprender o material.

Uma vez prometi a continuação deste artigo. Por fim, estou pronto para apresentar a você uma construção passo a passo de uma seção oblíqua de uma peça, mais próxima do nível de dever de casa. Além disso, a seção oblíqua é definida na terceira vista (a seção oblíqua é definida na vista esquerda)

ou anote nosso número de telefone e conte a seus amigos sobre nós - provavelmente alguém está procurando uma maneira de fazer desenhos

ou crie uma nota sobre nossas aulas em sua página ou blog - e outra pessoa poderá dominar o desenho.

Sim, está tudo bem, mas gostaria de ver como se faz a mesma coisa em uma peça mais complexa, com chanfros e furo em forma de cone, por exemplo.

Obrigado. Mas os reforços não estão eclodidos nos cortes?
Exatamente. São eles que não eclodem. Porque eles são regras gerais fazendo cortes. No entanto, eles geralmente são hachurados ao fazer cortes em projeções axonométricas - isometria, dimetria, etc. Ao executar seções inclinadas, a área relacionada ao reforço também é sombreada.

Obrigado, muito acessível. Você pode me dizer se a seção oblíqua pode ser feita na vista superior ou na vista esquerda? Em caso afirmativo, gostaria de ver o exemplo mais simples. Por favor.

É possível fazer tais cortes. Mas infelizmente não tenho um exemplo em mãos agora. E tem outro ponto interessante: por um lado, não há nada de novo aí, mas por outro lado, na prática, é realmente mais difícil desenhar essas seções. Por algum motivo, tudo começa a ficar confuso na cabeça e a maioria dos alunos tem dificuldades. Mas não desista!

Sim, está tudo bem, mas gostaria de ver como se faz a mesma coisa, mas com furos (transversais e não transversais), senão nunca vira uma elipse na minha cabeça

me ajude com um problema complexo

É uma pena que você escreveu aqui. Escreveríamos pelo correio - talvez tivéssemos tempo para discutir tudo.

Você explica bem. E se um dos lados da peça for semicircular? Além disso, existem furos na peça.

Ilya, use a lição da seção de geometria descritiva "Seção de um cilindro por um plano inclinado". Com ele, você pode descobrir o que fazer com furos (também são cilindros na verdade) e com um lado semicircular.

Agradeço ao autor pelo artigo! Breve e compreensível. Há cerca de 20 anos eu mesmo roía o granito da ciência, agora ajudo meu filho. Esqueci muito, mas seu artigo retornou uma compreensão fundamental do assunto. Vou lidar com a seção inclinada do cilindro)

Adicione seu comentário.

Axiomas da planimetria:

Em vários livros didáticos, as propriedades de retas e planos podem ser apresentadas de diferentes maneiras, na forma de um axioma, uma consequência dele, um teorema, um lema, etc. Considere o livro Pogorelov A.V.

A reta divide o plano em dois semiplanos.

De qualquer meia-linha a um dado meio-plano, pode-se traçar um ângulo com um dado medida de grau, menos de 180 0 , e apenas um.

Qualquer que seja o triângulo, existe um triângulo igual em um determinado local em relação à meia-linha dada.

Através de um ponto não pertencente a uma reta dada, no máximo uma reta pode ser traçada no plano paralelo à reta dada.

Axiomas da estereometria:

Seja qual for o plano, há pontos que pertencem a este plano, e pontos que não pertencem a este plano, e pontos que não pertencem a ele.

Se dois planos diferentes têm um ponto comum, eles se interceptam ao longo de uma linha reta que passa por esse ponto.

Se duas linhas diferentes têm um ponto comum, um plano pode ser traçado através delas e, além disso, apenas um.

Qualquer que seja a reta, há pontos que pertencem a esta reta e pontos que não pertencem a ela.

Através de quaisquer dois pontos você pode traçar uma linha, e apenas uma.

Dos três pontos em uma linha, um e apenas um fica entre os outros dois.

Cada segmento tem um certo comprimento maior que zero. O comprimento de um segmento é igual à soma dos comprimentos das partes em que é dividido por qualquer um de seus pontos.

Uma reta pertencente a um plano divide este plano em dois semiplanos.

Cada ângulo tem uma certa medida de grau maior que zero. O ângulo reto é 180 0 . A medida em graus de um ângulo é igual à soma das medidas em graus dos ângulos nos quais ele é dividido por qualquer raio que passe entre seus lados.

Em qualquer meia linha a partir de seu ponto de partida, você pode adiar um segmento de um determinado comprimento e apenas um.

A partir de uma meia linha no plano que a contém, um ângulo com uma determinada medida de grau menor que 180 pode ser plotado em um determinado meio plano 0 , e apenas um.

Seja qual for o triângulo, há um triângulo igual no plano dado em um determinado local em relação à meia-linha dada nesse plano.

Em um plano, através de um ponto dado não pertencente a uma reta dada, no máximo uma reta paralela à reta dada pode ser traçada.

corte transversal

No espaço, duas figuras, para o nosso caso, um plano e um poliedro podem ter o seguinte arranjo mútuo: não se cruzam, se cruzam em um ponto, se cruzam em linha reta e o plano intercepta o poliedro em seu interior (Fig. 1) , e ao mesmo tempo formam as seguintes figuras:

a) uma figura vazia (não se cruzam)

b) ponto

c) cortar

d) polígono

Se houver um polígono na interseção de um poliedro e um plano, então este polígonoé chamada de seção de um poliedro com um plano .

Figura 1

Definição. corte transversal um corpo espacial (por exemplo, um poliedro) é uma figura obtida na interseção de um corpo com um plano.

plano de corte poliedro Vamos chamar qualquer plano, em ambos os lados dos quais existem pontos de um determinado poliedro.

Consideraremos apenas o caso em que o plano intercepta o poliedro ao longo de seu interior. Nesse caso, a interseção desse plano com cada face do poliedro será um determinado segmento.

Se os planos se cruzam em uma linha reta, então a linha reta é chamadade um desses planos para outro.

No caso geral, o plano secante de um poliedro intercepta o plano de cada uma de suas faces (assim como qualquer outro plano secante desse poliedro). Ele também intercepta cada uma das linhas nas quais estão as arestas do poliedro.

A linha ao longo da qual o plano secante intercepta o plano de qualquer face do poliedro é chamadaseguindo o plano de corte no plano desta face, e o ponto no qual o plano secante intercepta a linha que contém qualquer aresta do poliedro é chamadoseguindo o plano de corte sobreesta linha reta. Este ponto também é o traço de uma linha reta no plano de corte. Se o plano de corte interceptar diretamente a face do poliedro, podemos falar sobre o traço do plano de corte na face e, da mesma forma, sobretraçado de um plano de corte em uma aresta de um poliedro, ou seja, o traço de uma aresta em um plano de corte.

Como uma reta é determinada unicamente por dois pontos, para encontrar o traço de um plano secante em qualquer outro plano e, em particular, no plano de qualquer face de um poliedro, basta construir dois pontos comuns dos planos

Para construir um traço de um plano secante, bem como para construir uma seção de um poliedro por este plano, não só o poliedro, mas também o plano secante deve ser especificado. E a construção do plano de seção ocorre dependendo da atribuição desse plano. As principais formas de definir um plano, e em particular um plano secante, são as seguintes:

três pontos que não estão em uma linha reta;

uma linha reta e um ponto que não está sobre ela;

duas linhas paralelas;

duas linhas que se cruzam;

um ponto e duas linhas que se cruzam;

Existem outras maneiras de definir o plano de corte.

Portanto, todos os métodos para construir seções de poliedros podem ser divididos em métodos.

Métodos para construir seções de poliedros

O método das seções de poliedros em estereometria é utilizado em problemas de construção. Baseia-se na capacidade de construir uma seção de um poliedro e determinar o tipo de seção.

Existem três métodos principais para a construção de seções de poliedros:

Método axiomático:

método de rastreamento.

Método combinado.

método coordenado.

Observação que o método dos traços e o método das seções auxiliares são variedadesMétodo axiomático de construção de secções.

Também podemos distinguir os seguintes métodos para construir seções de poliedros:

construção de uma secção de um poliedro por um plano que passa por um determinado ponto paralelo a um determinado plano;

construção de uma seção passando por uma determinada linha paralela a outra linha dada;

construção de uma seção passando por um ponto dado paralelo a duas retas enviesadas dadas;

construção de uma seção de um poliedro por um plano que passa por uma reta dada perpendicular a um plano dado;

construção de uma seção de um poliedro por um plano que passa por um ponto dado perpendicular a uma reta dada.

As principais ações que compõem os métodos de construção de seções são encontrar o ponto de interseção de uma reta com um plano, construir uma reta de interseção de dois planos, construir uma reta paralela a um plano perpendicular ao plano. Para construir uma linha reta de interseção de dois planos, geralmente são encontrados dois de seus pontos e uma linha reta é traçada através deles. Para construir o ponto de interseção de uma reta e um plano, encontre uma reta no plano que intercepte o dado. Então o ponto desejado é obtido na interseção da linha encontrada com a dada.

Considere listado separadamente por nósmétodos para construir seções de poliedros:

método de rastreamento.

método de rastreamento é baseado (operado) nos axiomas da estereometria, a essência do método é construir uma linha auxiliar, que é a imagem da linha de interseção do plano de corte com o plano de qualquer face da figura. É mais conveniente construir uma imagem da linha de interseção do plano de corte com o plano da base inferior. Está linhachamado de traço principal do plano de corte . Com o traço, é fácil construir imagens dos pontos do plano de corte localizados nas arestas laterais ou faces da figura. Conectando consistentemente as imagens desses pontos, obtemos a imagem da seção desejada.

Observação que ao construir o traço principal do plano secante, a seguinte declaração é usada.

Se os pontos pertencem ao plano secante e não pertencem a uma única linha reta, e sua projeção (central ou paralela) no plano escolhido como principal são, respectivamente, os pontos então os pontos de interseção das linhas correspondentes, ou seja, os pontos e estão na mesma linha (Fig. 1, a, b).

fig.1.a fig.1.b

Esta linha é o traço principal do plano de corte. Como os pontos estão no traço principal, basta encontrar dois desses três pontos para construí-lo.

Método das seções auxiliares.

Este método de construção de seções de poliedros é suficientemente universal. Nos casos em que o traço (ou traços) desejado do plano de corte está fora do desenho, esse método ainda apresenta algumas vantagens. Ao mesmo tempo, deve-se ter em mente que as construções realizadas com esse método costumam ser “lotadas”. No entanto, em alguns casos, o método das seções auxiliares acaba sendo o mais racional.

Método combinado

A essência do método combinado para a construção de seções de poliedros é a aplicação de teoremas sobre o paralelismo de linhas e planos no espaço em combinação com o método axiomático.

Método de coordenadas para a construção de seções.

A essência do método de coordenadas é calcular as coordenadas dos pontos de interseção das arestas ou um poliedro com um plano secante, que é dado pela equação do plano. A equação do plano de seção é calculada com base nas condições do problema.

Observação que este método de construção de uma seção de um poliedro é aceitável para um computador, pois está associado a uma grande quantidade de cálculos e, portanto, é aconselhável implementar esse método usando um computador.

Nossa principal tarefa será construir uma seção de um poliedro com um plano, ou seja, na construção da interseção desses dois conjuntos.

Construção de seções de poliedros

Antes de tudo, notamos que a seção de um poliedro convexo é um polígono plano convexo, cujos vértices no caso geral são os pontos de interseção do plano secante com as arestas do poliedro e os lados com suas faces.

Exemplos de criação de seção:

Há muitas maneiras diferentes de definir uma seção. O mais comum deles é o método de especificar um plano de corte por três pontos que não estão em uma linha reta.

Exemplo 1 Para a caixa ABCDA 1 B 1 C 1 D 1 . Construa uma seção passando pelos pontos M, N, L.

Solução:

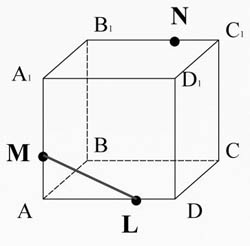
Conecte os pontos M e L no plano AA 1 D 1 D.

Intersectar a linha ML (pertencente à seção) com a aresta A 1 D 1 1 D 1 D. Obtenha o ponto X 1 .

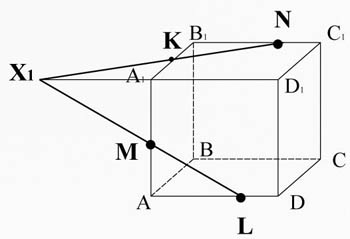
O ponto X1 está na aresta A 1 D 1 , e, portanto, os planos A 1 B 1 C 1 D 1 , conecte-o com um ponto N situado no mesmo plano.

x 1 N intercepta a aresta A 1 B 1 no ponto K.

Conecte os pontos K e M no mesmo plano AA 1 B 1 b.

Encontre a linha de interseção do plano de seção com o plano DD 1 C 1 C:

Interseção da linha ML (pertencente à seção) com a aresta DD 1 , eles estão no mesmo plano AA 1 D 1 D, pegue o ponto X 2 .

Intersectemos a linha KN (pertencente à seção) com a aresta D 1 C 1 , eles estão no mesmo plano A 1 B 1 C 1 D 1 , obtemos o ponto X3;

Os pontos X2 e X3 estão no plano DD 1 C 1 C. Desenhe uma linha X 2 x 3 , que intercepta a aresta C 1 C no ponto T, e a aresta DC no ponto P. E vamos conectar os pontos L e P, que estão no plano ABCD.

Assim, o problema é considerado resolvido se forem encontrados todos os segmentos ao longo dos quais o plano intercepta as faces do poliedro, o que fizemos. MKNTPL - seção desejada.

Observação. A mesma tarefa para a construção de uma seção pode ser resolvida usando a propriedade dos planos paralelos.

A partir do exposto, podemos compor um algoritmo (regra) para resolver problemas desse tipo.

Regras para a construção de seções de poliedros:

Exemplo 2 Deu, M

Resolvemos pelo método axiomático:

Desenhe um plano auxiliarDKM, que intercepta as arestas AB e BC nos pontos E eF(o curso da solução está na Fig. 2.). Vamos construir um "traço" do CM do plano de seção neste plano auxiliar, encontre o ponto de interseção do CM e EF- ponto P. Ponto P, bem comoeu, encontra-se no plano ABC, e é possível traçar uma linha reta ao longo da qual o plano de seção intercepta o plano ABC ("traço" da seção no plano ABC).

Exemplo 3 Nas arestas AB e AD da pirâmide MABCD, definimos os pontos P e Q, respectivamente, os pontos médios dessas arestas, e na aresta MC, definimos o ponto R. Vamos construir uma seção da pirâmide por um plano que passa pelos pontos P, Q e R.

A solução será realizada por um método combinado:

1). É claro que o traço principal do plano PQR é a linha PQ.

2). Encontre o ponto K no qual o plano MAC intercepta a linha PQ. Os pontos K e R pertencem tanto ao plano PQR quanto ao plano MAC. Portanto, traçando a reta KR, obtemos a linha de interseção desses planos.

3). Vamos encontrar o ponto N=AC BD, traçar a linha MN e encontrar o ponto F=KR MN.

4). O ponto F é ponto comum planos PQR e MDB, ou seja, esses planos se cruzam ao longo de uma linha reta que passa pelo ponto F. Ao mesmo tempo, como PQ é a linha média do triângulo ABD, então PQ é paralelo a BD, ou seja, a linha PQ também é paralelo ao plano MDB. Então o plano PQR passando pela linha PQ intercepta o plano MDB ao longo da linha paralela à linha PQ, ou seja, paralela à linha BD. Portanto, no plano MDB passando pelo ponto F traçamos uma reta paralela à reta BD.

5). Outras construções são claras a partir da figura. Como resultado, obtemos o polígono PQD"RB" - a seção necessária

Considere as seções do prisma para simplificar, ou seja, a conveniência do pensamento lógico, considere as seções do cubo (Fig. 3.a):

Arroz. 3.a

As seções do prisma por planos paralelos às arestas laterais são paralelogramos. Em particular, as seções diagonais são paralelogramos (Fig. 4).

Def. seção diagonal um prisma é uma seção por um plano que passa por duas arestas laterais que não pertencem à mesma face.

O polígono resultante de uma seção diagonal de um prisma é um paralelogramo. Questão sobre o número de seções diagonaisnO prisma angular é mais difícil do que a questão do número de diagonais. Haverá tantas seções quantas forem as diagonais na base. Sabemos que um prisma convexo tem polígonos convexos em suas bases, enquanto um prisma convexon-gon de diagonais. E assim podemos dizer que há metade das seções diagonais do número de diagonais.

Observação: Ao construir seções de um paralelepípedo na figura, deve-se levar em consideração o fato de que, se o plano de corte intercepta duas faces opostas ao longo de alguns segmentos, esses segmentos são paralelos “pela propriedade do paralelepípedo, ou seja, As faces opostas de um paralelepípedo são paralelas e iguais.

Nós fornecemos respostas para perguntas frequentes:

Que polígonos são obtidos na seção de um cubo por um plano?

"triângulo, quadrilátero, pentágono, hexágono".

Uma seção transversal plana de um cubo pode produzir um heptágono? E o octógono?

"não pode".

3) Surge a pergunta, qual é o maior número de lados de um polígono obtido por uma seção de um poliedro com um plano?

Maior número lados do polígono obtido na seção do poliedro pelo plano é igual ao número de faces do poliedro .

Exemplo 3 Construa uma seção do prisma A 1 B 1 C 1 D 1 ABCD por um plano que passa por três pontos M, N, K.

Considere o caso da localização dos pontos M, N, K na superfície de um prisma (Fig. 5).

Considere o caso: Neste caso é óbvio que M1 = B1.

Prédio:

Exemplo 4 Construa uma seção do paralelepípedo ABCDA 1 B 1 C 1 D 1 um plano passando pelos pontos M, N, P (os pontos são indicados no desenho (Fig. 6)).

Solução:

Arroz. 6

Os pontos N e P estão no plano da seção e no plano da base inferior do paralelepípedo. Vamos construir uma reta passando por esses pontos. Esta linha é o traço do plano secante no plano da base do paralelepípedo.

Continuemos a linha sobre a qual está o lado AB do paralelepípedo. As retas AB e NP se interceptam em algum ponto S. Este ponto pertence ao plano de corte.

Como o ponto M também pertence ao plano de seção e intercepta a linha AA 1 em algum ponto x.

Os pontos X e N estão no mesmo plano da face AA 1 D 1 D, conecte-os e pegue a linha XN.

Como os planos das faces do paralelepípedo são paralelos, é possível traçar uma reta passando pelo ponto M na face A 1 B 1 C 1 D 1 paralelo à linha NP. Esta linha cruzará o lado B 1 COM 1 no ponto Y.

Da mesma forma, desenhamos a linha YZ, paralela à linha XN. Conectamos Z com P e obtemos a seção desejada - MYZPNX.

As seções da pirâmide por planos que passam pelo topo são triângulos. Em particular, seções diagonais são triângulos. Estas são seções por planos que passam por duas arestas laterais não adjacentes da pirâmide.

Exemplo 4 Construa uma seção da pirâmide ABCDum plano passando pelos pontos K,eu, M.

Solução:

Vamos resolver o mesmo exemplo de forma diferente. .

Suponhamos que para os pontos K,eu, e Ü a seçãoKLNM(Fig. 7). denotar porFo ponto de interseção das diagonais do quadriláteroKLNM. Vamos desenhar uma linha retaD.F.e denotar porF 1 seu ponto de interseção com a face ABC. PontoF 1 coincide com o ponto de interseção das linhas AM e SK (F 1 pertence simultaneamente aos planos AMDEDSC). ApontarF 1 fácil de construir. Em seguida, construímos um pontoFcomo ponto de interseçãoD.F. 1 ELM. Em seguida, encontramos o pontoN.

O método considerado é chamadométodo de design interno . (para o nosso caso nós estamos falando sobre desenho central. quadriláterokISA é a projeção de um quadriláteroKMNLde um pontoD. Neste caso, o ponto de intersecção das diagonaisKMNL- pontoF- vai até o ponto de interseção das diagonais do quadriláterokISA - pontoF 1 .

Área da seção de um poliedro.

O problema de calcular a área da seção transversal de um poliedro geralmente é resolvido em várias etapas. Se o problema diz que a seção é construída (ou que o plano de corte é desenhado, etc.), na primeira etapa da solução, a forma da figura obtida na seção é encontrada.

Isso deve ser feito para selecionar a fórmula apropriada para calcular a área da seção transversal. Depois que a forma da figura obtida na seção é esclarecida e a fórmula para calcular a área dessa figura é escolhida, eles seguem diretamente para o trabalho computacional.

Em alguns casos, pode ser mais fácil se, sem descobrir a forma da figura obtida na seção, passarmos imediatamente ao cálculo de sua área usando a fórmula que segue do teorema.

O teorema sobre a área da projeção ortogonal de um polígono: a área da projeção ortogonal de um polígono sobre um plano é igual ao produto de sua área pelo cosseno do ângulo entre o plano do polígono e o plano de projeção: .

Uma fórmula válida para calcular a área da seção transversal é: onde é a área da projeção ortogonal da figura obtida na seção e é o ângulo entre o plano secante e o plano no qual a figura é projetada. Com tal solução, é necessário construir uma projeção ortogonal da figura obtida na seção e calcular

Se a condição do problema diz que a seção precisa ser construída e a área da seção obtida deve ser encontrada, no primeiro estágio é razoável construir a seção em questão e, naturalmente, determinar a forma de a figura obtida na seção, etc.

Observamos o seguinte fato: como se constroem seções de poliedros convexos, o polígono da seção também será convexo, portanto sua área pode ser encontrada dividindo-o em triângulos, ou seja, a área da seção é igual à soma das áreas dos triângulos de que é composto.

Tarefa 1.

– correto pirâmide triangular com um lado da base igual e igual a uma altura Construa uma seção da pirâmide por um plano passando pelos pontos, onde é o ponto médio do lado, e encontre sua área (Fig. 8).

Solução.

A seção transversal da pirâmide é um triângulo. Vamos encontrar sua área.

Como a base da pirâmide é um triângulo equilátero e o ponto é o ponto médio do lado, então é a altura e então, .

A área de um triângulo pode ser encontrada:

Tarefa 2.

costela lateral de um prisma regular é igual ao lado da base. Construir seções de um prisma por planos que passam por um pontoA, perpendicular à linha Se você encontrar a área da seção resultante do prisma.

Solução.

Vamos construir a seção dada. Façamos isso a partir de considerações puramente geométricas, por exemplo, como segue.

Em um plano que passa por uma determinada linha e um determinado ponto, traçamos uma linha perpendicular à linha (Fig. 9) passando por esse ponto. Usemos para isso o fato de que no triângulo ou seja, sua mediana também é a altura desse triângulo. Assim, uma linha reta.

Através do ponto, desenhamos outra linha perpendicular à linha. Vamos desenhá-lo, por exemplo, em um plano passando por uma linha reta. É claro que esta linha é uma linha

Assim, duas linhas que se cruzam, perpendiculares à linha, são construídas. Essas retas definem um plano que passa por um ponto perpendicular à reta, ou seja, é dado um plano secante.

Construímos uma seção do prisma por este plano. Observe que, como a reta é paralela ao plano. Então o plano que passa pela linha intercepta o plano ao longo de uma linha paralela à linha, ou seja, a linha. Desenhe uma linha reta através do ponto e conecte o ponto resultante com um ponto.

Quadrilátero dada secção. Vamos determinar sua área.

É claro que um quadrilátero é um retângulo, ou seja, sua área

arroz. 9

CONSTRUÇÃO DE SEÇÕES E SEÇÕES EM DESENHOS

O desenho da peça é formado adicionando sequencialmente as projeções, cortes e cortes necessários. Inicialmente, uma visualização personalizada é criada com um modelo especificado pelo usuário e a orientação do modelo é definida para melhor se adequar à visualização principal. Além disso, os cortes e seções necessários são criados para este e os seguintes tipos.

A vista principal (vista frontal) é selecionada de forma a dar a ideia mais completa das formas e dimensões da peça.

Seções em desenhos

Dependendo da posição do plano de corte, distinguem-se os seguintes tipos de cortes:

A) horizontal, se o plano de corte for paralelo ao plano de projeção horizontal;

B) vertical, se o plano de corte for perpendicular ao plano de projeção horizontal;

C) inclinado - o plano de corte é inclinado aos planos de projeção.

As seções verticais são divididas em:

· frontal - o plano de corte é paralelo ao plano de projeção frontal;

· perfil - o plano de corte é paralelo ao plano de projeção do perfil.
Dependendo do número de planos de corte, os cortes são:

· simples - com um plano de corte (Fig. 107);

· complexo - com dois ou mais planos de corte (Fig. 108)
A norma prevê os seguintes tipos de cortes complexos:

· escalonado, quando os planos secantes são paralelos (Fig. 108 a) e linhas quebradas - os planos secantes se cruzam (Fig. 108 b)

Fig.107 Corte simples

A) b)

Fig.108 Cortes complexos

Designação de cortes

No caso em que em uma seção simples o plano secante coincide com o plano de simetria do objeto, a seção não é indicada (Fig. 107). Em todos os outros casos, as seções são indicadas por letras maiúsculas do alfabeto russo, começando com a letra A, por exemplo, A-A.

A posição do plano de corte no desenho é indicada pela linha de corte - uma linha aberta espessada. Com um corte complexo, os golpes também são executados nas inflexões da linha de corte. As setas que indicam a direção da visão devem ser colocadas nos traços iniciais e finais, as setas devem estar a uma distância de 2-3 mm das extremidades externas dos traços. Do lado de fora de cada seta que indica a direção da visão, a mesma letra maiúscula é aplicada.

O mesmo botão é usado para designar cortes e seções no sistema KOMPAS Linha de corte localizada na página Legenda (fig.109).

Fig.109 Botão de linha de seção

Conectando meia vista a meia seção

Se a vista e a seção são figuras simétricas (Fig. 110), você pode conectar metade da vista e metade da seção, separando-as com uma linha fina tracejada, que é o eixo de simetria. Parte da seção geralmente é colocada à direita do eixo de simetria que separa a parte da vista da parte da seção ou abaixo do eixo de simetria. As linhas de contorno ocultas nas partes conectadas da vista e da seção geralmente não são mostradas. Se a linha axial que separa a vista e o corte coincide com a projeção de alguma linha, por exemplo, a aresta de uma figura facetada, então a vista e o corte são separados por uma linha ondulada sólida desenhada à esquerda do eixo de simetria se a borda está na superfície interna, ou à direita se a borda for externa.

Arroz. 110 Conectando parte de uma vista e uma seção

Cortes de construção

Estudaremos a construção de seções no sistema KOMPAS usando o exemplo de construção de um desenho de prisma, cuja tarefa é mostrada na Fig. 111.

A sequência do desenho é a seguinte:

1. Por dimensões dadas vamos construir um modelo sólido de um prisma (Fig. 109 b). Vamos salvar o modelo na memória do computador em um arquivo chamado "Prisma".

Fig.112 Painel de linhas

3. Para construir uma seção de perfil (Fig. 113) Desenhe uma linha seção A-A na vista principal usando o botão Linha de corte.

Fig.113 Construção de uma seção de perfil

A direção de visão e o texto da designação podem ser selecionados no painel de controle com o comando na parte inferior da tela (Fig. 114). A construção da linha de corte é concluída pressionando o botão Criar objeto.

Fig.114 Painel de controle para o comando de construção de cortes e seções

4. No painel Vistas associativas (Fig. 115), selecione o botão Linha de corte e especifique a linha de corte com a armadilha que aparece na tela. Se tudo for feito corretamente (a linha de corte deve ser desenhada na vista ativa), a linha de corte ficará vermelha. Depois de especificar a linha de corte A-A, um fantasma de imagem aparecerá na tela na forma de um retângulo geral.

Fig.115 Painel de vistas associativas

Com a ajuda da opção Corte/seção na barra de propriedades, o tipo de imagem é selecionado - Corte (Fig. 116) e a escala do corte exibido.

Fig.116 Painel de controle para o comando de construção de cortes e seções

A seção de perfil será construída automaticamente na conexão de projeção e com uma notação padrão. Se necessário, a conexão de projeção pode ser desligada pelo interruptor Conexão de projeção (Fig. 116). Para definir os parâmetros de hachura que serão utilizados na seção criada (seção), utilize os controles da aba Hachura.

Fig.117 Construção de uma seção horizontal B-B e seção C-C

Se o plano de corte selecionado ao construir o corte coincidir com o plano de simetria da peça, então, de acordo com o padrão, tal corte não é indicado. Mas se você simplesmente apagar a designação da seção, devido ao fato de que a exibição e a seção na memória do computador estão interconectadas, toda a seção será apagada. Portanto, para remover a designação, você deve primeiro destruir a conexão entre a vista e a seção. Para fazer isso, clique com o botão esquerdo do mouse para selecionar a seção e, a seguir, clique com o botão direito do mouse para abrir o menu de contexto, no qual o item de exibição Destroy é selecionado (Fig. 97). O símbolo da seção agora pode ser excluído.

5. Para construir uma seção horizontal, vamos desenhar uma linha de seção B-B através do plano inferior do furo na vista frontal. A vista frontal deve primeiro ser atualizada por dois cliques do botão esquerdo do mouse. Em seguida, uma seção horizontal é construída (Fig. 117).

6. Ao construir um corte frontal, uma parte da vista e uma parte do corte são compatíveis, pois são figuras simétricas. A borda externa do prisma é projetada na linha que separa a vista e o corte, então delimitamos vista e corte de uma linha ondulada fina sólida desenhada à direita do eixo de simetria, porque costela externa. O botão é usado para desenhar uma linha ondulada. Curva Bezier localizada no painel Geometry desenhada com o estilo For clipping line (Fig. 118). Especifique sequencialmente os pontos pelos quais a curva de Bezier deve passar. Para finalizar a execução do comando, clique no botão Criar objeto.

Fig.118 Selecionando um estilo de linha para uma quebra

Seccionando

Uma seção é uma imagem de um objeto que é obtida pela dissecação mental de um objeto com um plano. A seção mostra apenas o que está localizado no plano de corte.

A posição do plano de corte, com o qual a seção é formada, é indicada no desenho pela linha da seção, assim como nas seções.

As seções, dependendo de sua localização nos desenhos, são divididas em estendidas e sobrepostas. As seções removidas geralmente estão localizadas no campo livre do desenho e são contornadas pela linha principal. As seções sobrepostas são colocadas diretamente na imagem do objeto e contornadas com linhas finas (Fig. 119).

Fig.119 Construção de seções

Considere a sequência de construção de um desenho de um prisma com um oblíquo estendido seção B-B(Fig. 117).

1. Ative a vista frontal clicando duas vezes com o botão esquerdo do mouse na vista e desenhe uma linha de corte usando o botão Linha de corte . Vamos selecionar o texto da inscrição В-В.

2. Usando o botão Cut line localizado no painel Associative Views (Fig. 115), que aparece como uma armadilha, indique a linha secante planos B-B. Usando a opção Corte/seção na barra de propriedades, selecione o tipo de imagem - Seção (Fig. 116), a escala da seção exibida é selecionada na janela Escala.

A seção construída está localizada em uma relação de projeção, o que limita seu movimento no desenho, mas a relação de projeção pode ser desativada usando o botão conexão de projeção.

No desenho finalizado, desenhe linhas centrais, se necessário, insira as dimensões.

As tarefas para a construção de seções de poliedros levam lugar significativo como um curso de geometria escolar para o ensino médio e em exames em vários níveis. A resolução deste tipo de problemas contribui para a assimilação dos axiomas da estereometria, a sistematização de conhecimentos e competências, o desenvolvimento representação espacial e habilidades construtivas. As dificuldades que surgem na resolução de problemas na construção de seções são bem conhecidas.

De primeira infância enfrentamos cortes. Cortamos pão, linguiça e outros produtos, cortamos um palito ou lápis com uma faca. O plano secante em todos esses casos é o plano da faca. As seções (seções de peças) são diferentes.

A seção de um poliedro convexo é um polígono convexo, cujos vértices, no caso geral, são os pontos de interseção do plano de corte com as arestas do polígono, e os lados são as linhas de interseção do plano de corte com As caras.

Para construir uma linha de interseção de dois planos, basta encontrar dois pontos comuns desses planos e traçar uma linha através deles. Isso se baseia nas seguintes afirmações:

1. se dois pontos de uma reta pertencem a um plano, então toda a reta pertence a este plano;

2. se dois planos diferentes têm um ponto comum, eles se interceptam ao longo de uma linha reta que passa por esse ponto.

Como já disse, a construção de seções de poliedros pode ser realizada com base nos axiomas da estereometria e teoremas sobre o paralelismo de retas e planos. Ao mesmo tempo, existem certos métodos para construir seções planas de poliedros. Os três métodos a seguir são os mais eficazes:

método de rastreamento

Método de design interno

Método combinado.

No estudo da geometria e, em particular, nas seções dela onde as imagens são consideradas formas geométricas, imagens de formas geométricas auxiliam o uso de apresentações de computador. Com a ajuda de um computador, muitas aulas de geometria se tornam mais visuais e dinâmicas. Axiomas, teoremas, provas, tarefas de construção, tarefas de construção de seções podem ser acompanhadas por sucessivas construções na tela do monitor. Desenhos gerados por computador podem ser salvos e colados em outros documentos.

Quero mostrar alguns slides sobre o tema: "Construção de seções em corpos geométricos»

Para construir o ponto de interseção de uma reta e um plano, encontre uma reta no plano que intercepte a reta dada. Então o ponto desejado é o ponto de interseção da linha encontrada com a dada. Vamos ver nos próximos slides.

Tarefa 1.

Dois pontos M e N são marcados nas bordas do tetraedro DABC; M GAD, N b DC. Escolha o ponto de interseção da linha MN com o plano da base.

Solução: para encontrar o ponto de intersecção da linha MN com o plano

base continuaremos AC e segmento MN. Marquemos o ponto de interseção dessas linhas por X. O ponto X pertence à linha MN e à face AC, e AC está no plano da base, o que significa que o ponto X também está no plano da base . Portanto, o ponto X é o ponto de intersecção da linha MN com o plano da base.

Vamos considerar o segundo problema. Vamos complicar um pouco.

Tarefa 2.

Dado um tetraedro DABC de pontos M e N, onde M € DA, N C (DBC). Encontre o ponto de intersecção da linha MN com o plano ABC.

Solução: O ponto de interseção da linha MN com o plano ABC deve estar no plano que contém a linha MN e no plano da base. Continuamos o segmento DN até o ponto de interseção com a aresta DC. Marcamos o ponto de interseção por E. Continuamos a linha AE e MN até o ponto de interseção. Observe X. O ponto X pertence a MN, portanto está no plano que contém a reta MN e X pertence a AE, e AE está no plano ABC. Então X também está no plano ABC. Portanto, X é o ponto de interseção da linha MN e do plano ABC.

Vamos complicar a tarefa. Considere uma seção de figuras geométricas por planos que passam por três pontos dados.

Tarefa 3

Nas arestas AC, AD e DB do tetraedro DABC marcam-se os pontos M, N e P. Construir uma secção do tetraedro pelo plano MNP.

Solução: construa uma linha reta ao longo da qual o plano MNP. Intersecta o plano da face ABC. O ponto M é um ponto comum desses planos. Para construir outro ponto comum, continuamos o segmento AB e NP. Marcamos o ponto de interseção por X, que será o segundo ponto comum do plano MNP e ABC. Portanto, esses planos se cruzam ao longo da linha reta MX. MX intercepta a aresta BC em algum ponto E. Como E está sobre MX e MX é uma reta pertencente ao plano MNP, segue-se que PE pertence a MNP. O quadrilátero MNPE é a seção necessária.

Tarefa 4

Construímos uma seção de um prisma reto ABCA1B1C1 por um plano que passa pelos pontos P , Q,R, onde R pertence a ( AA 1C 1C), R pertence EM 1C1,

Q pertence a AB

Solução: Todos três pontos P,Q,R estão em faces diferentes, então ainda não podemos construir uma linha de interseção do plano secante com qualquer face do prisma. Vamos encontrar o ponto de interseção de PR com ABC. Vamos encontrar as projeções dos pontos P e R no plano de base PP1 perpendicular a BC e RR1 perpendicular a AC. A linha P1R1 intercepta a linha PR no ponto X. X é o ponto de interseção da linha PR com o plano ABC. Encontra-se no plano desejado K e no plano da base, como o ponto Q. XQ é uma linha reta que intercepta K com o plano da base. XQ intercepta AC no ponto K. Portanto, KQ é o segmento da interseção do plano X com a face ABC. K e R estão no plano X e no plano da face AA1C1C. Trace uma linha KR e marque o ponto de interseção com A1Q E. KE é a linha de interseção do plano X com esta face. Encontre a linha de interseção do plano X com o plano das faces BB1A1A. KE cruza com A1A no ponto Y. A linha QY é a linha de interseção do plano secante com o plano AA1B1B. FPEKQ - seção desejada.

As tarefas para construir seções de um cubo por um plano, via de regra, são mais simples do que, por exemplo, tarefas para seções de uma pirâmide.

Podemos traçar uma reta passando por dois pontos se eles estiverem no mesmo plano. Ao construir seções de um cubo, é possível mais uma opção para construir um traço de um plano de corte. Como o terceiro plano intercepta dois planos paralelos ao longo de linhas retas paralelas, se uma linha reta já foi construída em uma das faces e há um ponto na outra através do qual a seção passa, podemos traçar uma linha reta através este ponto paralelo ao dado.

Considere em exemplos concretos como construir seções de um cubo por um plano.

1) Construa uma seção do cubo por um plano passando pelos pontos A, C e M.

Problemas desse tipo são os mais simples de todos os problemas para a construção de seções de um cubo. Como os pontos A e C estão no mesmo plano (ABC), podemos traçar uma linha passando por eles. Seu traço é o segmento AC. É invisível, então representamos AC com um golpe. Da mesma forma, conectamos os pontos M e C, que estão no mesmo plano (CDD1), e os pontos A e M, que estão no mesmo plano (ADD1). Triângulo ACM é a seção necessária.

2) Construa uma seção do cubo por um plano passando pelos pontos M, N, P.

Aqui, apenas os pontos M e N estão no mesmo plano (ADD1), então traçamos uma linha reta através deles e obtemos o traço MN (invisível). Como as faces opostas do cubo estão em planos paralelos, o plano de corte intercepta os planos paralelos (ADD1) e (BCC1) ao longo de linhas paralelas. Já construímos uma das linhas paralelas - esta é a MN.

Através do ponto P traçamos uma linha paralela a MN. Ele intercepta a aresta BB1 no ponto S. PS é o traço do plano secante na face (BCC1).

Traçamos uma linha reta através dos pontos M e S, que estão no mesmo plano (ABB1). Obteve o rastreamento MS (visível).

Os planos (ABB1) e (CDD1) são paralelos. Já existe uma linha MS no plano (ABB1), então através do ponto N no plano (CDD1) desenhamos uma linha paralela a MS. Esta linha intercepta a aresta D1C1 no ponto L. Seu traço é NL (invisível). Os pontos P e L estão no mesmo plano (A1B1C1), então traçamos uma linha reta através deles.

O pentágono MNLPS é a seção necessária.

3) Construa uma seção do cubo por um plano passando pelos pontos M, N, P.

Os pontos M e N estão no mesmo plano (BCC1), então uma linha reta pode ser traçada através deles. Obtemos o traço MN (visível). O plano (BCC1) é paralelo ao plano (ADD1), então através do ponto P situado em (ADD1) traçamos uma linha paralela a MN. Ele intercepta a aresta AD no ponto E. Obtemos o traço PE (invisível).

Não há mais pontos no mesmo plano, nem uma reta e um ponto em planos paralelos. Portanto, uma das linhas já existentes deve ser continuada para obter um ponto adicional.

Se continuarmos a linha MN, então, como ela está no plano (BCC1), precisamos procurar o ponto de interseção de MN com uma das linhas desse plano. Já existem pontos de interseção com CC1 e B1C1 - estes são M e N. As linhas BC e BB1 permanecem. Continuamos BC e MN até a interseção no ponto K. O ponto K está na linha BC, o que significa que pertence ao plano (ABC), então podemos traçar uma linha através dele e o ponto E que está neste plano. Ele intercepta a aresta CD no ponto H. EH é seu traço (invisível). Como H e N estão no mesmo plano (CDD1), uma linha reta pode ser traçada através deles. Obtemos o traço HN (invisível).

Os planos (ABC) e (A1B1C1) são paralelos. Um deles contém a linha EH, o outro contém o ponto M. Podemos traçar uma linha passando por M paralela a EH. Obtemos o traço MF (visível). Traçamos uma reta passando pelos pontos M e F.

O hexágono MNHEPF é a seção necessária.

Se continuássemos a linha MN até a interseção com outra linha no plano (BCC1), com BB1, teríamos um ponto G pertencente ao plano (ABB1). Isso significa que através de G e P é possível traçar uma reta cujo traço é PF. Além disso, desenhamos linhas retas através de pontos situados em planos paralelos e chegamos ao mesmo resultado.

Trabalhar com linha reta PE dá a mesma seção transversal MNHEPF.

4) Construa uma seção do cubo por um plano passando pelo ponto M, N, P.

Aqui podemos traçar uma linha reta passando pelos pontos M e N no mesmo plano (A1B1C1). Sua pegada é MN (visível). Não há mais pontos no mesmo plano ou em planos paralelos.

Continuamos a linha MN. Encontra-se no plano (A1B1C1), pelo que só pode intersectar com uma das rectas deste plano. Já existem pontos de interseção com A1D1 e C1D1 - N e M. Mais duas linhas deste plano são A1B1 e B1C1. O ponto de interseção de A1B1 e MN é S. Como está na linha A1B1, pertence ao plano (ABB1), o que significa que uma linha pode ser traçada através dele e do ponto P, que está no mesmo plano. A linha PS intercepta a aresta AA1 no ponto E. PE é seu traço (visível). Através dos pontos N e E, situados no mesmo plano (ADD1), é possível traçar uma linha reta, cujo traço é NE (invisível). Há uma linha NE no plano (ADD1), e um ponto P no plano paralelo a ele (BCC1) Através do ponto P podemos traçar uma linha PL paralela a NE. Ela intercepta a aresta CC1 no ponto L. PL é o traço desta linha (visível). Os pontos M e L estão no mesmo plano (CDD1), o que significa que uma linha reta pode ser traçada através deles. A pegada dela é ML (invisível). O pentágono MLPEN é a seção necessária.

Foi possível continuar a linha NM em ambas as direções e procurar seus pontos de interseção não apenas com a linha A1B1, mas também com a linha B1C1, que também está no plano (A1B1C1). Nesse caso, traçamos duas retas passando pelo ponto P de uma só vez: uma no plano (ABB1) passando pelos pontos P e S, e a segunda no plano (BCC1), passando pelos pontos P e R. Depois disso , resta conectar os pontos situados no mesmo plano: M c L, E - com N.