घर › विद्युत उपकरण › भिन्नों का गुणन नियम और उदाहरण। विभिन्न भाजकों के साथ सरल और मिश्रित अंशों का गुणन

भिन्नों का गुणन नियम और उदाहरण। विभिन्न भाजकों के साथ सरल और मिश्रित अंशों का गुणन

इन रेक को पहले ही बायपास कर दें! 🙂

गुणन और अंशों का विभाजन।

ध्यान!
अतिरिक्त हैं
विशेष धारा 555 में सामग्री।
उन लोगों के लिए जो मजबूत हैं "बहुत नहीं। »
और उन लोगों के लिए जो "बहुत समान" हैं। "")

यह संक्रिया योग-घटाव से कहीं अधिक अच्छी है! क्योंकि यह आसान है। मैं आपको याद दिलाता हूं: एक अंश को एक अंश से गुणा करने के लिए, आपको अंशों को गुणा करना होगा (यह परिणाम का अंश होगा) और भाजक (यह भाजक होगा)। वह है:

सब कुछ अत्यंत सरल है. और कृपया एक सामान्य भाजक की तलाश न करें! यहां इसकी जरूरत नहीं...

एक अंश को एक अंश से विभाजित करने के लिए, आपको फ्लिप करने की आवश्यकता है दूसरा(यह महत्वपूर्ण है!) भिन्न करें और उन्हें गुणा करें, अर्थात:

यदि पूर्णांकों और भिन्नों के साथ गुणा या भाग पकड़ा जाता है, तो कोई बात नहीं। जोड़ की तरह, हम भाजक में एक इकाई के साथ एक पूरी संख्या से एक अंश बनाते हैं - और जाओ! उदाहरण के लिए:

हाई स्कूल में, आपको अक्सर तीन-कहानी (या यहां तक कि चार-कहानी!) के अंशों से निपटना पड़ता है। उदाहरण के लिए:

इस अंश को सभ्य रूप में कैसे लाया जाए? हाँ, बहुत आसान! दो बिंदुओं के माध्यम से विभाजन का प्रयोग करें:

लेकिन विभाजन आदेश के बारे में मत भूलना! गुणन के विपरीत, यह यहाँ बहुत महत्वपूर्ण है! निस्संदेह, हम 4:2 या 2:4 में भ्रमित नहीं होंगे। लेकिन तीन मंजिला अंश में गलती करना आसान है। कृपया ध्यान दें, उदाहरण के लिए:

पहले मामले में (बाईं ओर अभिव्यक्ति):

दूसरे में (दाईं ओर अभिव्यक्ति):

फर्क महसूस करो? 4 और 1/9!

विभाजन का क्रम क्या है? या कोष्ठक, या (यहाँ के रूप में) क्षैतिज डैश की लंबाई। एक आंख विकसित करें। और अगर कोई कोष्ठक या डैश नहीं हैं, जैसे:

फिर विभाजित-गुणा करें क्रम में, बाएं से दाएं!

और एक और बहुत ही सरल और महत्वपूर्ण ट्रिक। डिग्री वाले कार्यों में, यह आपके काम आएगा! आइए इकाई को किसी भिन्न से विभाजित करें, उदाहरण के लिए, 13/15 से:

शॉट पलट गया! और यह हमेशा होता है। 1 को किसी भी भिन्न से विभाजित करने पर परिणाम वही भिन्न होता है, केवल उलटा होता है।

अंशों के साथ यही सभी क्रियाएं हैं। बात काफी सरल है, लेकिन पर्याप्त से अधिक त्रुटियाँ देता है। टिप्पणी प्रायोगिक उपकरण, और वे (त्रुटियाँ) कम होंगी!

1. भिन्नात्मक भावों के साथ काम करते समय सबसे महत्वपूर्ण बात सटीकता और सावधानी है! ये सामान्य शब्द नहीं हैं, शुभ कामनाएँ नहीं हैं! यह एक सख्त जरूरत है! परीक्षा की सभी गणनाएँ एकाग्रता और स्पष्टता के साथ एक पूर्ण कार्य के रूप में करें। अपने सिर में गणना करते समय गड़बड़ करने की तुलना में ड्राफ्ट में दो अतिरिक्त पंक्तियां लिखना बेहतर होता है।

2. उदाहरणों में अलग - अलग प्रकारभिन्न - साधारण भिन्नों पर जाएँ।

3. हम सभी भिन्नों को अंत तक कम करते हैं।

4. हम दो बिंदुओं के माध्यम से विभाजन का उपयोग करके बहु-स्तरीय भिन्नात्मक भावों को सामान्य लोगों तक कम करते हैं (हम विभाजन के क्रम का पालन करते हैं!)।

यहां वे कार्य हैं जिन्हें आपको पूरा करने की आवश्यकता है। सभी कार्यों के बाद उत्तर दिए जाते हैं। इस विषय की सामग्री और व्यावहारिक सलाह का उपयोग करें। अनुमान लगाएं कि आप कितने उदाहरणों को सही ढंग से हल कर सकते हैं। पहली बार! बिना कैलकुलेटर के! और सही निष्कर्ष निकालें।

सही उत्तर याद रखें दूसरे (विशेष रूप से तीसरे) समय से प्राप्त - गिनती नहीं है!ऐसा कठोर जीवन है।

इसलिए, परीक्षा मोड में हल करें ! वैसे यह परीक्षा की तैयारी है। हम एक उदाहरण हल करते हैं, हम जांचते हैं, हम निम्नलिखित को हल करते हैं। हमने सब कुछ तय कर लिया - हमने पहली से आखिरी तक फिर से जाँच की। लेकिन केवल तबउत्तरों को देखो।

अपने से मेल खाने वाले उत्तरों की तलाश में। मैंने जानबूझकर उन्हें गड़बड़ी में लिखा, प्रलोभन से दूर, बोलने के लिए। यहाँ वे हैं, उत्तर, अर्धविराम द्वारा अलग किए गए।

0; 17/22; 3/4; 2/5; 1; 25.

और अब हम निष्कर्ष निकालते हैं। अगर सब कुछ काम कर गया - आपके लिए खुश! अंशों के साथ प्रारंभिक गणना आपकी समस्या नहीं है! आप अधिक गंभीर कार्य कर सकते हैं। अगर नहीं।

तो आपको दो में से एक समस्या है। या दोनों एक साथ।) ज्ञान की कमी और (या) असावधानी। लेकिन। यह व्याख्या करने योग्य समस्या।

विशेष खंड 555 "अंश" में इन सभी (और न केवल!) उदाहरणों का विश्लेषण किया गया है। क्या, क्यों और कैसे की विस्तृत व्याख्या के साथ। ऐसा विश्लेषण ज्ञान और कौशल की कमी के साथ बहुत मदद करता है!

हाँ, और दूसरी समस्या पर वहाँ कुछ है।) काफी व्यावहारिक सलाह, अधिक चौकस कैसे बनें. हां हां! सलाह जो लागू हो सकती है प्रत्येक.

ज्ञान और सावधानी के अलावा, सफलता के लिए एक निश्चित स्वचालितता की आवश्यकता होती है। इसे कहाँ से प्राप्त करें? मुझे एक भारी आह सुनाई देती है... हाँ, केवल व्यवहार में, और कहीं नहीं।

आप प्रशिक्षण के लिए साइट 321start.ru पर जा सकते हैं। वहां, "कोशिश करें" विकल्प में, सभी के उपयोग के लिए 10 उदाहरण हैं। तत्काल सत्यापन के साथ। पंजीकृत उपयोगकर्ताओं के लिए - 34 उदाहरण सरल से गंभीर तक। यह केवल अंशों के लिए है।

अगर आपको यह साइट पसंद है।

वैसे, मेरे पास आपके लिए कुछ और दिलचस्प साइटें हैं।)

यहां आप उदाहरणों को हल करने का अभ्यास कर सकते हैं और अपने स्तर का पता लगा सकते हैं। तत्काल सत्यापन के साथ परीक्षण। रुचि के साथ जानें!

और यहां आप कार्यों और डेरिवेटिव से परिचित हो सकते हैं।

नियम 1

एक अंश को एक प्राकृतिक संख्या से गुणा करने के लिए, आपको इसके अंश को इस संख्या से गुणा करना होगा, और भाजक को अपरिवर्तित छोड़ देना चाहिए।

नियम 2

किसी भिन्न को भिन्न से गुणा करने के लिए:

1. अंशों का गुणनफल और इन भिन्नों के हरों का गुणनफल ज्ञात कीजिए

2. पहले गुणनफल को अंश के रूप में और दूसरे गुणनफल को हर के रूप में लिखें।

नियम 3

मिश्रित संख्याओं को गुणा करने के लिए, आपको उन्हें अनुचित भिन्नों के रूप में लिखना होगा, और फिर भिन्नों को गुणा करने के नियम का उपयोग करना होगा।

नियम 4

एक अंश को दूसरे से विभाजित करने के लिए, आपको लाभांश को भाजक के व्युत्क्रम से गुणा करना होगा।

उदाहरण 1

गणना

उदाहरण 2

गणना

उदाहरण 3

गणना

उदाहरण 4

गणना

अंक शास्त्र। अन्य सामग्री

एक संख्या को एक तर्कसंगत शक्ति तक बढ़ाना। (

एक प्राकृतिक शक्ति के लिए एक संख्या बढ़ाना। (

बीजगणितीय असमानताओं को हल करने के लिए सामान्यीकृत अंतराल विधि (लेखक कोल्चानोव ए.वी.)

बीजगणितीय असमानताओं को हल करने में कारकों के प्रतिस्थापन की विधि (लेखक कोल्चानोव ए.वी.)

विभाज्यता के लक्षण (लुंगु अलीना)

'साधारण भिन्नों का गुणन और विभाजन' विषय पर स्वयं का परीक्षण करें

अंशों का गुणन

हम साधारण भिन्नों के गुणन पर कई संभावित तरीकों से विचार करेंगे।

एक भिन्न को एक भिन्न से गुणा करना

यह सबसे सरल मामला है, जिसमें आपको निम्नलिखित का उपयोग करने की आवश्यकता है अंश गुणन नियम.

को एक अंश को एक अंश से गुणा करें, ज़रूरी:

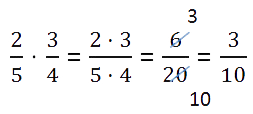
पहले भिन्न के अंश को दूसरे भिन्न के अंश से गुणा करें और उनके गुणनफल को नए भिन्न के अंश में लिखें;

पहले भिन्न के हर को दूसरे भिन्न के हर से गुणा करें और उनके गुणनफल को नए भिन्न के हर में लिखें;

अंशों और हरों को गुणा करने से पहले, जाँच लें कि क्या भिन्नों को घटाया जा सकता है। गणनाओं में अंशों को कम करने से आपकी गणनाओं में काफी सुविधा होगी।

एक अंश को एक प्राकृतिक संख्या से गुणा करना

अंश करना एक प्राकृतिक संख्या से गुणा करेंआपको भिन्न के अंश को इस संख्या से गुणा करने की आवश्यकता है, और भिन्न के हर को अपरिवर्तित रहने दें।

यदि गुणन का परिणाम एक अनुचित अंश है, तो इसे मिश्रित संख्या में बदलना न भूलें, अर्थात पूरे भाग का चयन करें।

मिश्रित संख्याओं का गुणन

मिश्रित संख्याओं को गुणा करने के लिए, आपको पहले उन्हें अनुचित भिन्नों में बदलना होगा और फिर साधारण भिन्नों को गुणा करने के नियम के अनुसार गुणा करना होगा।

एक अंश को एक प्राकृतिक संख्या से गुणा करने का दूसरा तरीका

कभी-कभी गणनाओं में एक साधारण अंश को एक संख्या से गुणा करने की एक अलग विधि का उपयोग करना अधिक सुविधाजनक होता है।

एक अंश को एक प्राकृतिक संख्या से गुणा करने के लिए, आपको अंश के हर को इस संख्या से विभाजित करने की आवश्यकता है, और अंश को समान रहने दें।

जैसा कि उदाहरण से देखा जा सकता है, नियम के इस संस्करण का उपयोग करना अधिक सुविधाजनक है यदि अंश का भाजक शेष के बिना एक प्राकृतिक संख्या से विभाज्य है।

एक अंश का एक संख्या से विभाजन

किसी भिन्न को किसी संख्या से विभाजित करने का सबसे तेज़ तरीका क्या है? आइए सिद्धांत का विश्लेषण करें, एक निष्कर्ष निकालें और उदाहरणों का उपयोग करके देखें कि एक नए छोटे नियम के अनुसार किसी संख्या द्वारा अंश का विभाजन कैसे किया जा सकता है।

आमतौर पर, एक संख्या द्वारा एक अंश का विभाजन अंशों के विभाजन के नियम के अनुसार किया जाता है। पहली संख्या (अंश) को दूसरे के व्युत्क्रम से गुणा किया जाता है। चूंकि दूसरी संख्या एक पूर्णांक है, इसका व्युत्क्रम एक अंश है, जिसका अंश एक के बराबर है, और भाजक है दिया गया नंबर. योजनाबद्ध रूप से, एक अंश को एक प्राकृतिक संख्या से विभाजित करना इस तरह दिखता है:

इससे हम निष्कर्ष निकालते हैं:

किसी भिन्न को किसी संख्या से विभाजित करने के लिए, हर को उस संख्या से गुणा करें और अंश को वही रहने दें। नियम को और भी संक्षेप में तैयार किया जा सकता है:

जब आप किसी भिन्न को किसी संख्या से विभाजित करते हैं, तो वह संख्या हर में चली जाती है।

अंश को संख्या से विभाजित करें:

एक अंश को एक संख्या से विभाजित करने के लिए, हम अंश को अपरिवर्तित फिर से लिखते हैं, और हर को इस संख्या से गुणा करते हैं। हम 6 और 3 को 3 से घटाते हैं।

किसी भिन्न को किसी संख्या से विभाजित करते समय, हम अंश को फिर से लिखते हैं और भाजक को उस संख्या से गुणा करते हैं। हम 16 और 24 को 8 से घटाते हैं।

किसी भिन्न को किसी संख्या से भाग देने पर वह संख्या हर में चली जाती है, इसलिए हम अंश को वही छोड़ देते हैं, और भाजक को भाजक से गुणा कर देते हैं। हम 21 और 35 को 7 से घटाते हैं।

गुणन और अंशों का विभाजन

पिछली बार हमने भिन्नों को जोड़ना और घटाना सीखा था (पाठ "भिन्नों को जोड़ना और घटाना" देखें)। उन क्रियाओं में सबसे कठिन क्षण भिन्नों को एक आम भाजक में लाना था।

अब गुणा और भाग से निपटने का समय आ गया है। अच्छी खबर यह है कि ये ऑपरेशन जोड़ और घटाव से भी आसान हैं। आरंभ करने के लिए, विचार करें सबसे सरल मामला, जब एक विशिष्ट पूर्णांक भाग के बिना दो सकारात्मक अंश होते हैं।

दो भिन्नों का गुणा करने के लिए, आपको उनके अंशों और हरों को अलग-अलग गुणा करना होगा। पहली संख्या नए अंश का अंश होगी, और दूसरी संख्या भाजक होगी।

दो अंशों को विभाजित करने के लिए, आपको पहले अंश को "उल्टे" दूसरे से गुणा करना होगा।

परिभाषा से यह इस प्रकार है कि अंशों का विभाजन गुणा करने के लिए घटाया जाता है। किसी भिन्न को फ़्लिप करने के लिए, केवल अंश और हर की अदला-बदली करें। इसलिए, पूरे पाठ में हम मुख्य रूप से गुणन पर विचार करेंगे।

गुणन के परिणामस्वरूप, एक घटा हुआ अंश उत्पन्न हो सकता है (और अक्सर उत्पन्न होता है) - बेशक, इसे कम किया जाना चाहिए। यदि, सभी कटौती के बाद, अंश गलत निकला, तो इसमें पूरे भाग को प्रतिष्ठित किया जाना चाहिए। लेकिन गुणा के साथ वास्तव में क्या नहीं होगा एक आम भाजक में कमी: कोई क्रॉसवाइड तरीके नहीं, अधिकतम कारक और कम से कम सामान्य गुणक।

काम। व्यंजक का मान ज्ञात कीजिए:

परिभाषा के अनुसार हमारे पास है:

एक पूर्णांक भाग और नकारात्मक अंशों के साथ अंशों का गुणन

यदि अंशों में एक पूर्णांक भाग है, तो उन्हें अनुचित में परिवर्तित किया जाना चाहिए - और उसके बाद ही ऊपर उल्लिखित योजनाओं के अनुसार गुणा किया जाना चाहिए।

यदि किसी भिन्न के अंश में, हर में या उसके सामने ऋण हो, तो उसे निम्नलिखित नियमों के अनुसार गुणन की सीमा से बाहर या पूरी तरह से हटाया जा सकता है:

प्लस बार माइनस माइनस देता है;
दो नकारात्मक एक सकारात्मक बनाते हैं।

अब तक, इन नियमों का सामना केवल नकारात्मक अंशों को जोड़ने और घटाने के दौरान ही किया जाता था, जब पूरे भाग से छुटकारा पाने की आवश्यकता होती थी। एक उत्पाद के लिए, उन्हें एक साथ कई मिन्यूज़ "बर्न" करने के लिए सामान्यीकृत किया जा सकता है:

जब तक वे पूरी तरह से गायब नहीं हो जाते, तब तक हम जोड़े में माइनस को पार करते हैं। एक चरम मामले में, एक ऋण जीवित रह सकता है - वह जो एक मैच नहीं मिला;
यदि कोई माइनस नहीं बचा है, तो ऑपरेशन पूरा हो गया है - आप गुणा करना शुरू कर सकते हैं। यदि अंतिम माइनस को पार नहीं किया गया है, क्योंकि उसे एक जोड़ी नहीं मिली, हम इसे गुणन की सीमा से बाहर कर देते हैं। आपको एक नकारात्मक अंश मिलता है।

हम सभी अंशों को अनुचित में अनुवादित करते हैं, और फिर हम गुणन की सीमा से बाहर के ऋणों को निकालते हैं। जो बचा है उसे गुणा किया जाता है सामान्य नियम. हम पाते हैं:

मैं आपको एक बार फिर से याद दिला दूं कि हाइलाइट किए गए पूर्णांक भाग वाले अंश से पहले आने वाला माइनस विशेष रूप से पूरे अंश को संदर्भित करता है, न कि केवल इसके पूर्णांक भाग को (यह पिछले दो उदाहरणों पर लागू होता है)।

नकारात्मक संख्याओं पर भी ध्यान दें: जब गुणा किया जाता है, तो वे कोष्ठक में संलग्न होते हैं। ऐसा इसलिए किया जाता है ताकि माइनस को गुणन चिह्नों से अलग किया जा सके और पूरे अंकन को अधिक सटीक बनाया जा सके।

मक्खी पर अंशों को कम करना

गुणन एक बहुत ही श्रमसाध्य ऑपरेशन है। यहां संख्याएं काफी बड़ी हैं, और कार्य को आसान बनाने के लिए, आप अंश को और भी कम करने का प्रयास कर सकते हैं गुणन से पहले. वास्तव में, संक्षेप में, अंशों के अंश और भाजक सामान्य कारक हैं, और इसलिए, उन्हें भिन्न की मूल संपत्ति का उपयोग करके कम किया जा सकता है। उदाहरणों पर एक नज़र डालें:

सभी उदाहरणों में, जो संख्याएँ घटाई गई हैं और जो बची हैं उन्हें लाल रंग से चिह्नित किया गया है।

कृपया ध्यान दें: पहले मामले में, गुणक पूरी तरह से कम हो गए थे। इकाइयाँ अपने स्थान पर बनी रहीं, जिन्हें सामान्यतया छोड़ा जा सकता है। दूसरे उदाहरण में पूर्ण कमीहासिल करना संभव नहीं था, लेकिन गणना की कुल राशि अभी भी कम हो गई थी।

हालाँकि, किसी भी स्थिति में भिन्नों को जोड़ते और घटाते समय इस तकनीक का उपयोग न करें! हां, कभी-कभी समान संख्याएं होती हैं जिन्हें आप केवल कम करना चाहते हैं। यहाँ, देखें:

आप ऐसा नहीं कर सकते!

त्रुटि इस तथ्य के कारण होती है कि अंश जोड़ते समय, योग भिन्न के अंश में दिखाई देता है, न कि संख्याओं के गुणनफल में। इसलिए, इस संपत्ति के बाद से, एक अंश की मुख्य संपत्ति को लागू करना असंभव है हम बात कर रहे हैंयह संख्याओं को गुणा करने के बारे में है।

अंशों को कम करने का कोई अन्य कारण नहीं है, इसलिए पिछली समस्या का सही समाधान इस तरह दिखता है:

जैसा कि आप देख सकते हैं, सही उत्तर इतना सुंदर नहीं निकला। सामान्य तौर पर, सावधान रहें।

अंशों का विभाजन।

एक अंश का एक प्राकृतिक संख्या से विभाजन।

एक अंश को एक प्राकृतिक संख्या से विभाजित करने के उदाहरण

एक अंश द्वारा एक प्राकृतिक संख्या का विभाजन।

एक प्राकृतिक संख्या को एक अंश से विभाजित करने के उदाहरण

साधारण अंशों का विभाजन।

साधारण अंशों के विभाजन के उदाहरण

मिश्रित संख्याओं का विभाजन।

मिश्रित भिन्नों को अनुचित में परिवर्तित करें;
पहले अंश को दूसरे के व्युत्क्रम से गुणा करें;
परिणामी अंश को कम करें;
यदि आपको एक अनुचित अंश मिलता है, तो अनुचित अंश को मिश्रित में परिवर्तित करें।

मिश्रित संख्याओं को विभाजित करने के उदाहरण

1 1 2: 2 2 3 = 1 2 + 1 2: 2 3 + 2 3 = 3 2: 8 3 = 3 2 3 8 = 3 3 2 8 = 9 16

2 1 7: 3 5 = 2 7 + 1 7: 3 5 = 15 7: 3 5 = 15 7 5 3 = 15 5 7 3 = 5 5 7 = 25 7 = 7 3 + 4 7 = 3 4 7

किसी भी अश्लील टिप्पणी को हटा दिया जाएगा और उनके लेखकों को ब्लैकलिस्ट कर दिया जाएगा!

ऑनलाइनएमस्कूल में आपका स्वागत है.
मेरा नाम दोवज़िक मिखाइल विक्टरोविच है। मैं इस साइट का मालिक और लेखक हूं, मैंने पूरी लिखी है सैद्धांतिक सामग्री, साथ ही ऑनलाइन अभ्यास और कैलकुलेटर जिनका उपयोग आप गणित का अध्ययन करने के लिए कर सकते हैं।

अंश। गुणन और अंशों का विभाजन।

एक भिन्न को एक भिन्न से गुणा करना।

साधारण अंशों को गुणा करने के लिए, अंश को अंश से गुणा करना आवश्यक है (हमें गुणनफल का अंश प्राप्त होता है) और भाजक को भाजक से (हमें गुणनफल का भाजक मिलता है)।

अंश गुणन सूत्र:

अंशों और हरों के गुणन के साथ आगे बढ़ने से पहले, अंश को कम करने की संभावना की जांच करना आवश्यक है। यदि आप अंश को कम करने का प्रबंधन करते हैं, तो आपके लिए गणना करना जारी रखना आसान होगा।

टिप्पणी! एक सामान्य भाजक की तलाश करने की कोई आवश्यकता नहीं है !!

एक साधारण अंश का एक अंश से विभाजन।

एक साधारण भिन्न का एक भिन्न से विभाजन इस प्रकार होता है: दूसरे भिन्न को पलट दें (अर्थात् अंश और हर को स्थानों में बदल दें) और उसके बाद भिन्नों का गुणा किया जाता है।

साधारण अंशों को विभाजित करने का सूत्र:

एक अंश को एक प्राकृतिक संख्या से गुणा करना।

टिप्पणी!एक अंश को एक प्राकृतिक संख्या से गुणा करते समय, अंश के अंश को हमारी प्राकृतिक संख्या से गुणा किया जाता है, और भिन्न का हर समान रहता है। यदि उत्पाद का परिणाम एक अनुचित अंश है, तो गलत अंश को मिश्रित अंश में बदलकर पूरे भाग का चयन करना सुनिश्चित करें।

एक प्राकृतिक संख्या को शामिल करने वाले अंशों का विभाजन।

यह उतना डरावना नहीं है जितना लगता है। जोड़ के मामले में, हम एक पूर्णांक को हर में एक इकाई के साथ एक भिन्न में परिवर्तित करते हैं। उदाहरण के लिए:

मिश्रित अंशों का गुणन।

भिन्नों को गुणा करने के नियम (मिश्रित):

मिश्रित भिन्नों को अनुचित में परिवर्तित करें;
अंशों के अंश और हर को गुणा करें;
हम अंश को कम करते हैं;
यदि हमें एक अनुचित अंश मिलता है, तो हम अनुचित अंश को मिश्रित अंश में बदल देते हैं।

टिप्पणी!एक मिश्रित अंश को दूसरे मिश्रित अंश से गुणा करने के लिए, आपको पहले उन्हें अनुचित अंशों के रूप में लाना होगा, और फिर साधारण अंशों को गुणा करने के नियम के अनुसार गुणा करना होगा।

एक अंश को एक प्राकृतिक संख्या से गुणा करने का दूसरा तरीका।

किसी साधारण अंश को किसी संख्या से गुणा करने की दूसरी विधि का उपयोग करना अधिक सुविधाजनक है।

टिप्पणी!एक अंश को एक प्राकृतिक संख्या से गुणा करने के लिए, अंश के भाजक को इस संख्या से विभाजित करना आवश्यक है, और अंश को अपरिवर्तित छोड़ दें।

उपरोक्त उदाहरण से, यह स्पष्ट है कि यह विकल्प उपयोग करने के लिए अधिक सुविधाजनक है जब किसी भिन्न के हर को बिना शेषफल के एक प्राकृतिक संख्या से विभाजित किया जाता है।

बहुस्तरीय अंश।

हाई स्कूल में, तीन मंजिला (या अधिक) अंश अक्सर पाए जाते हैं। उदाहरण:

इस तरह के एक अंश को उसके सामान्य रूप में लाने के लिए, 2 बिंदुओं के विभाजन का उपयोग किया जाता है:

टिप्पणी!भिन्नों को विभाजित करते समय, विभाजन का क्रम बहुत महत्वपूर्ण होता है। सावधान रहें, यहां भ्रमित होना आसान है।

टिप्पणी, उदाहरण के लिए:

एक को किसी भिन्न से विभाजित करने पर, परिणाम वही भिन्न होगा, केवल उल्टा:

भिन्नों को गुणा करने और विभाजित करने के लिए व्यावहारिक सुझाव:

1. भिन्नात्मक भावों के साथ काम करने में सबसे महत्वपूर्ण बात सटीकता और सावधानी है। सभी गणनाओं को सावधानीपूर्वक और सटीक, एकाग्र और स्पष्ट रूप से करें। अपने सिर में गणनाओं में भ्रमित होने की तुलना में एक मसौदे में कुछ अतिरिक्त पंक्तियाँ लिखना बेहतर है।

2. विभिन्न प्रकार के भिन्नों वाले कार्यों में, साधारण भिन्नों के प्रकार पर जाएँ।

3. हम सभी अंशों को तब तक कम करते हैं जब तक कि कम करना संभव न हो।

4. हम 2 बिंदुओं के माध्यम से विभाजन का उपयोग करते हुए बहु-स्तरीय भिन्नात्मक भावों को सामान्य में लाते हैं।

के तहत और अप करने के लिए नहीं- गीत "स्प्रिंग टैंगो" (समय आता है - दक्षिण से पक्षी आते हैं) - संगीत। Valery Milyaev मैंने गलत सुना, मैंने गलत समझा, मैं पकड़ में नहीं आया, इस अर्थ में कि मैंने अनुमान नहीं लगाया, मैंने सभी क्रियाओं को अलग से नहीं लिखा, मुझे उपसर्ग के बारे में पता नहीं था-। ऐसा होता है, […]
पृष्ठ नहीं मिला तीसरी अंतिम रीडिंग में, विशेष प्रशासनिक क्षेत्रों (SAR) के निर्माण के लिए प्रदान करने वाले सरकारी दस्तावेजों के एक पैकेज को अपनाया गया था। यूरोपीय संघ से बाहर निकलने के कारण, यूके को यूरोपीय वैट क्षेत्र में शामिल नहीं किया जाएगा और […]
संयुक्त जांच समिति गिरावट में दिखाई देगी
एल्गोरिथम पेटेंट एल्गोरिथम पेटेंट कैसा दिखता है एल्गोरिथम पेटेंट कैसे तैयार किया जा रहा है तकनीकी विवरणविशेष रूप से पेटेंट कराने के प्रयोजनों के लिए संकेतों और/या डेटा को संग्रहीत करने, संसाधित करने और प्रसारित करने के तरीकों में आमतौर पर कोई विशेष कठिनाई नहीं होती है, और […]
पेंशन पर नए मसौदे के बारे में जानना महत्वपूर्ण है 12 दिसंबर, 1993 रूसी संघ का गठन (30 दिसंबर, 2008 को रूसी संघ के संविधान में संशोधन पर रूसी संघ के कानूनों द्वारा किए गए संशोधनों के अधीन एन 6- FKZ, दिनांक 30 दिसंबर, 2008 N 7-FKZ, […]
एक महिला के लिए सेवानिवृत्ति के बारे में डिटिज दिन के एक पुरुष नायक के लिए शांत हैं - दिन के एक महिला नायक के लिए कोरस में - सेवानिवृत्त महिलाओं के लिए समर्पण हास्य है पेंशनभोगियों के लिए प्रतियोगिताएं दिलचस्प होंगी प्रिय मित्रों! एक पल का ध्यान! सनसनी! केवल […]

औसत के दौरान और उच्च विद्यालयछात्र "अंश" विषय से गुजरे। हालाँकि, यह अवधारणा सीखने की प्रक्रिया में दी गई तुलना में बहुत व्यापक है। आज, एक अंश की अवधारणा का अक्सर सामना किया जाता है, और हर कोई किसी भी अभिव्यक्ति की गणना नहीं कर सकता है, उदाहरण के लिए, अंशों को गुणा करना।

अंश क्या है?

ऐसा ऐतिहासिक रूप से हुआ कि मापने की आवश्यकता के कारण भिन्नात्मक संख्याएँ दिखाई दीं। जैसा कि अभ्यास से पता चलता है, एक खंड की लंबाई, एक आयताकार आयत का आयतन निर्धारित करने के लिए अक्सर उदाहरण होते हैं।

प्रारंभ में, छात्रों को शेयर के रूप में इस तरह की अवधारणा से परिचित कराया जाता है। उदाहरण के लिए, यदि आप एक तरबूज को 8 भागों में बांटते हैं, तो प्रत्येक को तरबूज का आठवां हिस्सा मिलेगा। आठ के इस एक हिस्से को शेयर कहा जाता है।

किसी भी मूल्य के ½ के बराबर शेयर को आधा कहा जाता है; ⅓ - तीसरा; ¼ - एक चौथाई। 5/8, 4/5, 2/4 जैसी प्रविष्टियाँ सामान्य भिन्न कहलाती हैं। एक साधारण भिन्न को एक अंश और एक भाजक में विभाजित किया जाता है। उनके बीच एक भिन्नात्मक रेखा, या भिन्नात्मक रेखा है। एक भिन्नात्मक दंड को क्षैतिज या तिरछी रेखा के रूप में खींचा जा सकता है। में इस मामले मेंयह विभाजन चिह्न के लिए खड़ा है।

भाजक दर्शाता है कि मूल्य कितने बराबर शेयरों में बांटा गया है; और अंश यह है कि कितने बराबर शेयर लिए गए हैं। भिन्नात्मक पट्टी के ऊपर अंश लिखा होता है, उसके नीचे भाजक।

साधारण भिन्नों को एक निर्देशांक किरण पर दिखाना सबसे सुविधाजनक होता है। यदि एक खंड को 4 बराबर भागों में बांटा गया है, तो प्रत्येक हिस्से को नामित करें लैटिन पत्र, तो परिणामस्वरूप आप एक उत्कृष्ट प्राप्त कर सकते हैं दृश्य सामग्री. तो, बिंदु A संपूर्ण इकाई खंड के 1/4 के बराबर एक हिस्सा दिखाता है, और बिंदु B इस खंड के 2/8 को चिह्नित करता है।

अंशों की किस्में

अंश सामान्य, दशमलव और मिश्रित संख्याएँ हैं। इसके अलावा, अंशों को उचित और अनुचित में विभाजित किया जा सकता है। यह वर्गीकरण साधारण भिन्नों के लिए अधिक उपयुक्त है।

एक उचित भिन्न वह संख्या है जिसका अंश भाजक से छोटा होता है। तदनुसार, एक अनुचित अंश एक संख्या है जिसका अंश भाजक से अधिक है। दूसरे प्रकार को आमतौर पर मिश्रित संख्या के रूप में लिखा जाता है। इस तरह की अभिव्यक्ति में एक पूर्णांक भाग और एक भिन्नात्मक भाग होता है। उदाहरण के लिए, 1½। 1 - पूर्णांक भाग, ½ - भिन्नात्मक। हालाँकि, यदि आपको अभिव्यक्ति के साथ कुछ जोड़तोड़ करने की आवश्यकता है (भिन्नों को विभाजित करना या गुणा करना, उन्हें कम करना या परिवर्तित करना), तो मिश्रित संख्या को एक अनुचित अंश में बदल दिया जाता है।

एक सही आंशिक अभिव्यक्ति हमेशा एक से कम होती है, और एक गलत एक हमेशा 1 से अधिक या उसके बराबर होती है।

इस अभिव्यक्ति के लिए, वे एक रिकॉर्ड को समझते हैं जिसमें किसी भी संख्या का प्रतिनिधित्व किया जाता है, जिसके भिन्नात्मक अभिव्यक्ति के भाजक को कई शून्यों के साथ एक के माध्यम से व्यक्त किया जा सकता है। यदि अंश सही है, तो दशमलव अंकन में पूर्णांक भाग शून्य होगा।

दशमलव लिखने के लिए, आपको पहले पूर्णांक भाग लिखना होगा, इसे अल्पविराम से भिन्नात्मक से अलग करना होगा, और फिर भिन्नात्मक व्यंजक लिखना होगा। यह याद रखना चाहिए कि अल्पविराम के बाद अंश में उतने ही संख्यात्मक वर्ण होने चाहिए जितने हर में शून्य होते हैं।

उदाहरण. दशमलव अंकन में अंश 7 21/1000 का प्रतिनिधित्व करें।

गलत भिन्न को मिश्रित संख्या में बदलने के लिए एल्गोरिथम और इसके विपरीत

समस्या के उत्तर में अनुचित अंश लिखना गलत है, इसलिए इसे मिश्रित संख्या में बदलना चाहिए:

अंश को मौजूदा भाजक से विभाजित करें;
वी विशिष्ट उदाहरणअधूरा भागफल - संपूर्ण;
और शेष भिन्नात्मक भाग का अंश है, जिसमें भाजक अपरिवर्तित रहता है।

उदाहरण. अनुचित अंश को मिश्रित संख्या में बदलें: 47/5।

समाधान. 47: 5. अधूरा भागफल 9 है, शेष = 2. इसलिए, 47/5 = 9 2/5।

कभी-कभी आपको एक मिश्रित संख्या को अनुचित अंश के रूप में प्रस्तुत करने की आवश्यकता होती है। फिर आपको निम्नलिखित एल्गोरिदम का उपयोग करने की आवश्यकता है:

पूर्णांक भाग को भिन्नात्मक अभिव्यक्ति के भाजक से गुणा किया जाता है;
परिणामी उत्पाद अंश में जोड़ा जाता है;
परिणाम अंश में लिखा जाता है, भाजक अपरिवर्तित रहता है।

उदाहरण. संख्या को मिश्रित रूप में एक अनुचित अंश के रूप में व्यक्त करें: 9 8 / 10।

समाधान. 9 x 10 + 8 = 90 + 8 = 98 अंश है।

उत्तर: 98 / 10.

साधारण अंशों का गुणन

आप साधारण भिन्नों पर विभिन्न बीजगणितीय संक्रियाएँ कर सकते हैं। दो संख्याओं को गुणा करने के लिए, आपको अंश को अंश से और हर को हर से गुणा करना होगा। इसके अलावा, अंशों का गुणन विभिन्न भाजकसमान भाजक वाली भिन्नात्मक संख्याओं के गुणनफल से भिन्न नहीं होता है।

ऐसा होता है कि परिणाम खोजने के बाद, आपको अंश को कम करने की आवश्यकता होती है। जितना संभव हो परिणामी अभिव्यक्ति को सरल बनाना अत्यावश्यक है। बेशक, यह नहीं कहा जा सकता है कि उत्तर में एक अनुचित अंश एक गलती है, लेकिन इसे सही उत्तर कहना भी मुश्किल है।

उदाहरण. दो साधारण भिन्नों का गुणनफल ज्ञात कीजिए: ½ और 20/18।

जैसा कि उदाहरण से देखा जा सकता है, उत्पाद खोजने के बाद, एक कम करने योग्य भिन्नात्मक संकेतन प्राप्त होता है। इस मामले में अंश और भाजक दोनों 4 से विभाज्य हैं, और परिणाम 5/9 का उत्तर है।

दशमलव अंशों का गुणन

दशमलव भिन्नों का गुणनफल अपने सिद्धांत में साधारण भिन्नों के गुणनफल से काफी भिन्न होता है। तो, अंशों को गुणा करना इस प्रकार है:

दो दशमलव अंशों को एक दूसरे के नीचे लिखा जाना चाहिए ताकि सबसे दाहिने अंक एक दूसरे के नीचे हों;
आपको अल्पविराम के बावजूद, प्राकृतिक संख्याओं के रूप में, लिखित संख्याओं को गुणा करने की आवश्यकता है;
प्रत्येक संख्या में अल्पविराम के बाद अंकों की संख्या गिनें;
गुणन के बाद प्राप्त परिणाम में, आपको दशमलव बिंदु के बाद दोनों कारकों में योग में निहित कई डिजिटल वर्णों को दाईं ओर गिनने की आवश्यकता है, और एक अलग चिन्ह लगाएं;
यदि गुणनफल में कम अंक हैं, तो इस संख्या को कवर करने के लिए उनके सामने इतने शून्य लिखे जाने चाहिए, एक अल्पविराम लगाएं और शून्य के बराबर एक पूर्णांक भाग निर्दिष्ट करें।

उदाहरण. दो दशमलवों के उत्पाद की गणना करें: 2.25 और 3.6।

समाधान.

मिश्रित अंशों का गुणन

दो मिश्रित अंशों के उत्पाद की गणना करने के लिए, आपको भिन्नों को गुणा करने के नियम का उपयोग करने की आवश्यकता है:

मिश्रित संख्याओं को अनुचित भिन्नों में परिवर्तित करें;
अंशों का गुणनफल ज्ञात कीजिए;
भाजक का गुणनफल ज्ञात कीजिए;
परिणाम लिखो;
जितना हो सके अभिव्यक्ति को सरल बनाएं।

उदाहरण. 4½ और 6 2/5 का गुणनफल ज्ञात कीजिए।

एक संख्या को एक अंश से गुणा करना (एक संख्या से भिन्न)

दो भिन्नों, मिश्रित संख्याओं का गुणनफल ज्ञात करने के अलावा, ऐसे कार्य भी हैं जिनमें आपको एक भिन्न से गुणा करने की आवश्यकता होती है।

तो, एक दशमलव अंश और एक प्राकृतिक संख्या का गुणनफल ज्ञात करने के लिए, आपको चाहिए:

अंश के नीचे संख्या लिखिए ताकि सबसे दाहिने अंक एक के ऊपर एक हों;
अल्पविराम के बावजूद काम खोजें;
प्राप्त परिणाम में, अंश में दशमलव बिंदु के बाद वर्णों की संख्या को दाईं ओर गिनते हुए, अल्पविराम का उपयोग करके पूर्णांक भाग को भिन्नात्मक भाग से अलग करें।

गुणा करने के लिए सामान्य अंशएक संख्या से, आपको अंश और प्राकृतिक कारक का गुणनफल ज्ञात करना चाहिए। अगर उत्तर कम करने योग्य अंश है, तो इसे परिवर्तित किया जाना चाहिए।

उदाहरण. 5/8 और 12 के गुणनफल की गणना करें।

समाधान. 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.

उत्तर: 7 1 / 2.

जैसा कि आप पिछले उदाहरण से देख सकते हैं, परिणामी परिणाम को कम करना और गलत आंशिक अभिव्यक्ति को मिश्रित संख्या में बदलना आवश्यक था।

साथ ही, भिन्नों का गुणनफल किसी संख्या के गुणनफल को मिश्रित रूप और एक प्राकृतिक गुणनखंड में ज्ञात करने पर भी लागू होता है। इन दो संख्याओं को गुणा करने के लिए, आपको मिश्रित कारक के पूर्णांक भाग को संख्या से गुणा करना चाहिए, अंश को समान मान से गुणा करना चाहिए, और भाजक को अपरिवर्तित छोड़ देना चाहिए। यदि आवश्यक हो, तो आपको यथासंभव परिणाम को सरल बनाने की आवश्यकता है।

उदाहरण. 9 5/6 और 9 का गुणनफल ज्ञात कीजिए।

समाधान. 9 5/6 x 9 \u003d 9 x 9 + (5 x 9) / 6 \u003d 81 + 45/6 \u003d 81 + 7 3/6 \u003d 88 1/2।

उत्तर: 88 1 / 2.

10, 100, 1000 या 0.1 कारकों से गुणा; 0.01; 0.001

निम्नलिखित नियम पिछले पैराग्राफ से अनुसरण करता है। एक दशमलव अंश को 10, 100, 1000, 10000, आदि से गुणा करने के लिए, आपको अल्पविराम को दाईं ओर ले जाने की आवश्यकता है क्योंकि गुणक में एक के बाद शून्य हैं।

उदाहरण 1. 0.065 और 1000 का गुणनफल ज्ञात कीजिए।

समाधान. 0.065 x 1000 = 0065 = 65।

उत्तर: 65.

उदाहरण 2. 3.9 और 1000 का गुणनफल ज्ञात कीजिए।

समाधान. 3.9 x 1000 = 3.900 x 1000 = 3900।

उत्तर: 3900.

यदि आपको एक प्राकृतिक संख्या और 0.1 गुणा करने की आवश्यकता है; 0.01; 0.001; 0.0001, आदि, आपको परिणामी उत्पाद में अल्पविराम को बाईं ओर ले जाना चाहिए क्योंकि एक से पहले शून्य हैं। यदि आवश्यक हो, तो एक प्राकृतिक संख्या के सामने पर्याप्त संख्या में शून्य लिखे जाते हैं।

उदाहरण 1. 56 और 0.01 का गुणनफल ज्ञात कीजिए।

समाधान. 56 x 0.01 = 0056 = 0.56।

उत्तर: 0,56.

उदाहरण 2. 4 और 0.001 का गुणनफल ज्ञात कीजिए।

समाधान. 4 x 0.001 = 0004 = 0.004।

उत्तर: 0,004.

इसलिए, विभिन्न भिन्नों का गुणनफल ज्ञात करने में कठिनाई नहीं आनी चाहिए, सिवाय शायद परिणाम की गणना के; इस मामले में, आप कैलकुलेटर के बिना बस नहीं कर सकते।

पाठ सामग्री

समान भाजक वाले भिन्नों को जोड़ना

भिन्नों को जोड़ना दो प्रकार का होता है:

समान भाजक वाले भिन्नों को जोड़ना
विभिन्न भाजक के साथ भिन्नों को जोड़ना

आइए समान हर वाले भिन्नों को जोड़ना शुरू करें। यहाँ सब कुछ सरल है। समान भाजक वाले भिन्नों को जोड़ने के लिए, आपको उनके अंशों को जोड़ना होगा, और भाजक को अपरिवर्तित रहने देना होगा। उदाहरण के लिए, चलिए भिन्नों और को जोड़ते हैं। हम अंशों को जोड़ते हैं और भाजक को अपरिवर्तित छोड़ देते हैं:

इस उदाहरण को आसानी से समझा जा सकता है अगर हम एक ऐसे पिज़्ज़ा के बारे में सोचें जो चार भागों में बंटा हो। यदि आप पिज़्ज़ा में पिज़्ज़ा जोड़ते हैं, तो आपको पिज़्ज़ा मिलता है:

उदाहरण 2भिन्न जोड़ें और।

उत्तर एक अनुचित अंश है। यदि कार्य का अंत आता है, तो अनुचित अंशों से छुटकारा पाने की प्रथा है। अनुचित अंश से छुटकारा पाने के लिए, आपको इसमें पूरे भाग का चयन करना होगा। हमारे मामले में, पूर्णांक भाग आसानी से आवंटित किया जाता है - दो को दो से विभाजित करना एक के बराबर है:

इस उदाहरण को आसानी से समझा जा सकता है अगर हम दो हिस्सों में बंटे पिज्जा के बारे में सोचें। अगर आप पिज़्ज़ा में और पिज़्ज़ा जोड़ते हैं, तो आपको एक पूरा पिज़्ज़ा मिलता है:

उदाहरण 3. भिन्न जोड़ें और।

दोबारा, अंशों को जोड़ें, और भाजक को अपरिवर्तित छोड़ दें:

इस उदाहरण को आसानी से समझा जा सकता है अगर हम एक ऐसे पिज़्ज़ा के बारे में सोचें जो तीन हिस्सों में बंटा हो। अगर आप पिज़्ज़ा में और पिज़्ज़ा जोड़ते हैं, तो आपको पिज़्ज़ा मिलता है:

उदाहरण 4एक व्यंजक का मान ज्ञात कीजिए

यह उदाहरण पिछले वाले की तरह ही हल किया गया है। अंशों को जोड़ा जाना चाहिए और भाजक को अपरिवर्तित छोड़ दिया जाना चाहिए:

आइए चित्र का उपयोग करके हमारे समाधान को चित्रित करने का प्रयास करें। अगर आप पिज़्ज़ा में पिज़्ज़ा जोड़ते हैं और ज़्यादा पिज़्ज़ा जोड़ते हैं, तो आपको 1 पूरा पिज़्ज़ा और ज़्यादा पिज़्ज़ा मिलता है।

जैसा कि आप देख सकते हैं, समान भाजक वाले भिन्नों को जोड़ना कठिन नहीं है। निम्नलिखित नियमों को समझना पर्याप्त है:

समान भाजक वाले भिन्नों को जोड़ने के लिए, आपको उनके अंशों को जोड़ना होगा, और भाजक को अपरिवर्तित रहने देना होगा;

विभिन्न भाजक के साथ भिन्नों को जोड़ना

अब हम सीखेंगे कि अलग-अलग हर वाले भिन्नों को कैसे जोड़ा जाता है। भिन्नों को जोड़ते समय, उन भिन्नों के हर समान होने चाहिए। लेकिन वे हमेशा एक जैसे नहीं होते।

उदाहरण के लिए, भिन्नों को जोड़ा जा सकता है क्योंकि उनके हर समान होते हैं।

लेकिन भिन्नों को एक साथ नहीं जोड़ा जा सकता, क्योंकि इन भिन्नों के हर अलग-अलग होते हैं। ऐसे मामलों में, भिन्नों को समान (सामान्य) हर में घटाया जाना चाहिए।

भिन्नों को एक ही भाजक में कम करने के कई तरीके हैं। आज हम उनमें से केवल एक पर विचार करेंगे, क्योंकि शुरुआती के लिए बाकी तरीके जटिल लग सकते हैं।

इस पद्धति का सार इस तथ्य में निहित है कि दोनों भिन्नों के हर के पहले (एलसीएम) की मांग की जाती है। फिर LCM को पहले भिन्न के हर से विभाजित किया जाता है और पहला अतिरिक्त गुणक प्राप्त होता है। वे दूसरे अंश के साथ भी ऐसा ही करते हैं - LCM को दूसरे भिन्न के भाजक से विभाजित किया जाता है और दूसरा अतिरिक्त कारक प्राप्त होता है।

फिर अंशों के अंश और हर को उनके अतिरिक्त कारकों से गुणा किया जाता है। इन क्रियाओं के परिणामस्वरूप, भिन्न भाजक वाले अंश समान भाजक वाले भिन्नों में बदल जाते हैं। और हम पहले से ही जानते हैं कि ऐसे भिन्नों को कैसे जोड़ा जाता है।

उदाहरण 1. भिन्न जोड़ें और

सबसे पहले, हम दोनों भिन्नों के हरों का लघुत्तम समापवर्त्य ज्ञात करते हैं। पहले भिन्न का भाजक संख्या 3 है, और दूसरे भिन्न का हर संख्या 2 है। इन संख्याओं का लघुत्तम समापवर्तक 6 है

एलसीएम (2 और 3) = 6

अब वापस भिन्नों पर और। सबसे पहले, हम LCM को पहले भिन्न के हर से विभाजित करते हैं और पहला अतिरिक्त गुणनखंड प्राप्त करते हैं। LCM संख्या 6 है, और पहले भिन्न का हर संख्या 3 है। 6 को 3 से विभाजित करें, हमें 2 मिलता है।

परिणामी संख्या 2 पहला अतिरिक्त कारक है। हम इसे पहले अंश में लिखते हैं। ऐसा करने के लिए, हम अंश के ऊपर एक छोटी तिरछी रेखा बनाते हैं और इसके ऊपर पाया गया अतिरिक्त कारक लिखते हैं:

हम दूसरे अंश के साथ भी ऐसा ही करते हैं। हम लघुत्तम समापवर्त्य को दूसरे भिन्न के हर से विभाजित करते हैं और दूसरा अतिरिक्त गुणनखंड प्राप्त करते हैं। LCM संख्या 6 है, और दूसरे भिन्न का हर संख्या 2 है। 6 को 2 से विभाजित करें, हमें 3 मिलता है।

परिणामी संख्या 3 दूसरा अतिरिक्त कारक है। हम इसे दूसरे भिन्न में लिखते हैं। फिर से, हम दूसरे अंश के ऊपर एक छोटी तिरछी रेखा बनाते हैं और इसके ऊपर पाया गया अतिरिक्त कारक लिखते हैं:

अब हम जोड़ने के लिए पूरी तरह तैयार हैं। यह अंशों के अंशों और हरों को उनके अतिरिक्त कारकों से गुणा करने के लिए बना हुआ है:

हम जो आए हैं, उस पर करीब से नज़र डालें। हम इस नतीजे पर पहुंचे कि जिन भिन्नों के हर अलग-अलग थे, वे भिन्नों में बदल गईं जिनके हर समान थे। और हम पहले से ही जानते हैं कि ऐसे भिन्नों को कैसे जोड़ा जाता है। आइए इस उदाहरण को अंत तक पूरा करें:

इस प्रकार उदाहरण समाप्त होता है। जोड़ने के लिए यह निकला।

आइए चित्र का उपयोग करके हमारे समाधान को चित्रित करने का प्रयास करें। अगर आप पिज़्ज़ा में पिज़्ज़ा जोड़ते हैं, तो आपको एक पूरा पिज़्ज़ा और दूसरा पिज़्ज़ा का छठा हिस्सा मिलता है:

भिन्नों को समान (सामान्य) हर में घटाना भी एक चित्र का उपयोग करके दर्शाया जा सकता है। भिन्नों और एक सामान्य भाजक को लाने पर, हम भिन्न और प्राप्त करते हैं। इन दो अंशों को पिज़्ज़ा के समान स्लाइस द्वारा दर्शाया जाएगा। अंतर केवल इतना होगा कि इस बार उन्हें समान भागों में विभाजित किया जाएगा (समान भाजक तक घटाया जाएगा)।

पहला चित्र एक अंश (छह में से चार टुकड़े) दिखाता है और दूसरा चित्र एक अंश (छह में से तीन टुकड़े) दिखाता है। इन टुकड़ों को एक साथ रखने पर हमें (छह में से सात टुकड़े) मिलते हैं। यह भिन्न गलत है, इसलिए हमने इसमें पूर्णांक भाग को हाइलाइट किया है। परिणाम था (एक पूरा पिज़्ज़ा और दूसरा छठा पिज़्ज़ा)।

ध्यान दें कि हमने पेंट किया है उदाहरण दियाबहुत विस्तृत। में शिक्षण संस्थानोंइतने विस्तृत तरीके से लिखना प्रथागत नहीं है। आपको दोनों भाजक और उनके अतिरिक्त गुणनखंडों का लघुत्तम समापवर्त्य शीघ्रता से ज्ञात करने में सक्षम होने की आवश्यकता है, साथ ही साथ अपने अंशों और हरों द्वारा पाए गए अतिरिक्त गुणनखंडों को शीघ्रता से गुणा करने में सक्षम होना चाहिए। स्कूल में रहते हुए हमें इस उदाहरण को इस प्रकार लिखना होगा:

लेकिन वहाँ भी है पीछे की ओरपदक। यदि गणित के अध्ययन के पहले चरण में विस्तृत नोट्स नहीं बनाए गए हैं, तो इस तरह के प्रश्न "वह संख्या कहाँ से आती है?", "अचानक अंश पूरी तरह से भिन्न अंशों में क्यों बदल जाते हैं? «.

विभिन्न भाजक के साथ अंशों को जोड़ना आसान बनाने के लिए, आप निम्न चरण-दर-चरण निर्देशों का उपयोग कर सकते हैं:

भिन्नों के हरों का लघुत्तम समापवर्त्य ज्ञात कीजिए;
LCM को प्रत्येक भिन्न के हर से विभाजित करें और प्रत्येक भिन्न के लिए एक अतिरिक्त गुणक प्राप्त करें;
भिन्नों के अंशों और हरों को उनके अतिरिक्त गुणनखंडों से गुणा करें;
समान भाजक वाले भिन्नों को जोड़ें;
यदि उत्तर एक अनुचित अंश निकला, तो उसके पूरे भाग का चयन करें;

उदाहरण 2एक व्यंजक का मान ज्ञात कीजिए .

आइए ऊपर दिए गए निर्देशों का उपयोग करें।

चरण 1. भिन्नों के हरों का लघुत्तम समापवर्त्य ज्ञात कीजिए

दोनों भिन्नों के हरों का लघुत्तम समापवर्त्य ज्ञात कीजिए। भिन्नों के हर 2, 3 और 4 संख्याएँ हैं

चरण 2. लघुत्तम समापवर्त्य को प्रत्येक भिन्न के हर से विभाजित करें और प्रत्येक भिन्न के लिए एक अतिरिक्त गुणक प्राप्त करें

LCM को पहले भिन्न के हर से विभाजित करें। एलसीएम संख्या 12 है, और पहले भिन्न का भाजक संख्या 2 है। 12 को 2 से विभाजित करें, हमें 6 मिलता है। हमें पहला अतिरिक्त कारक 6 मिला। हम इसे पहले भिन्न पर लिखते हैं:

अब हम लघुत्तम समापवर्त्य को दूसरे भिन्न के हर से विभाजित करते हैं। LCM संख्या 12 है, और दूसरे भिन्न का हर 3 है। 12 को 3 से विभाजित करें, हमें 4 मिलता है। हमें दूसरा अतिरिक्त कारक 4 मिला। हम इसे दूसरे भिन्न पर लिखते हैं:

अब हम LCM को तीसरे भिन्न के हर से विभाजित करते हैं। लघुत्तम समापवर्तक संख्या 12 है, और तीसरे भिन्न का भाजक संख्या 4 है। 12 को 4 से विभाजित करें, हमें 3 मिलता है। हमें तीसरा अतिरिक्त कारक 3 मिला। हम इसे तीसरे भिन्न पर लिखते हैं:

चरण 3. भिन्नों के अंश और हर को अपने अतिरिक्त गुणनखंडों से गुणा करें

हम अंशों और हरों को अपने अतिरिक्त गुणनखंडों से गुणा करते हैं:

चरण 4. समान भाजक वाले भिन्नों को जोड़ें

हम इस निष्कर्ष पर पहुंचे कि जिन भिन्नों के हर अलग-अलग थे, वे भिन्नों में बदल गए जिनके समान (सामान्य) भाजक हैं। इन अंशों को जोड़ना बाकी है। जोड़ें:

जोड़ना एक पंक्ति में फ़िट नहीं हुआ, इसलिए हमने शेष व्यंजक को अगली पंक्ति में स्थानांतरित कर दिया। गणित में इसकी अनुमति है। जब कोई व्यंजक एक पंक्ति में फिट नहीं होता है, तो उसे अगली पंक्ति में ले जाया जाता है, और पहली पंक्ति के अंत में और नई पंक्ति की शुरुआत में एक समान चिह्न (=) लगाना आवश्यक होता है। दूसरी पंक्ति पर समान चिह्न इंगित करता है कि यह पहली पंक्ति पर मौजूद अभिव्यक्ति की निरंतरता है।

चरण 5. यदि उत्तर अनुचित अंश निकला, तो उसमें पूरे भाग का चयन करें

हमारा उत्तर एक अनुचित अंश है। हमें इसके पूरे हिस्से को सिंगल करना होगा। हम हाइलाइट करते हैं:

उत्तर मिला

समान भाजक वाले भिन्नों का घटाव

अंश घटाव दो प्रकार के होते हैं:

समान भाजक वाले भिन्नों का घटाव
विभिन्न भाजक के साथ अंशों का घटाव

पहले, आइए जानें कि समान हर वाले भिन्नों को कैसे घटाया जाता है। यहाँ सब कुछ सरल है। एक अंश में से दूसरे को घटाने के लिए, आपको दूसरे भिन्न के अंश को पहले भिन्न के अंश से घटाना होगा और भाजक को वही रहने देना होगा।

उदाहरण के लिए, आइए अभिव्यक्ति का मान ज्ञात करें। इस उदाहरण को हल करने के लिए, दूसरे भिन्न के अंश को पहले भिन्न के अंश से घटाना आवश्यक है, और भाजक को अपरिवर्तित छोड़ दें। आओ इसे करें:

इस उदाहरण को आसानी से समझा जा सकता है अगर हम एक ऐसे पिज़्ज़ा के बारे में सोचें जो चार भागों में बंटा हो। यदि आप पिज़्ज़ा से पिज़्ज़ा काटते हैं, तो आपको पिज़्ज़ा मिलता है:

उदाहरण 2व्यंजक का मान ज्ञात कीजिए।

दोबारा, पहले अंश के अंश से, दूसरे अंश के अंश को घटाएं और भाजक को अपरिवर्तित छोड़ दें:

इस उदाहरण को आसानी से समझा जा सकता है अगर हम एक ऐसे पिज़्ज़ा के बारे में सोचें जो तीन हिस्सों में बंटा हो। यदि आप पिज़्ज़ा से पिज़्ज़ा काटते हैं, तो आपको पिज़्ज़ा मिलता है:

उदाहरण 3एक व्यंजक का मान ज्ञात कीजिए

यह उदाहरण पिछले वाले की तरह ही हल किया गया है। पहले अंश के अंश से, आपको शेष अंशों के अंशों को घटाना होगा:

जैसा कि आप देख सकते हैं, समान भाजक वाले भिन्नों को घटाने में कुछ भी जटिल नहीं है। निम्नलिखित नियमों को समझना पर्याप्त है:

एक अंश से दूसरे को घटाने के लिए, आपको पहले भिन्न के अंश से दूसरे भिन्न के अंश को घटाना होगा, और भाजक को अपरिवर्तित रहने देना होगा;
यदि उत्तर एक अनुचित अंश निकला, तो आपको इसमें पूरे भाग का चयन करना होगा।

विभिन्न भाजक के साथ अंशों का घटाव

उदाहरण के लिए, एक भिन्न को एक भिन्न से घटाया जा सकता है, क्योंकि इन भिन्नों के हर समान होते हैं। लेकिन एक भिन्न को एक भिन्न से घटाया नहीं जा सकता, क्योंकि इन भिन्नों के हर अलग-अलग होते हैं। ऐसे मामलों में, भिन्नों को समान (सामान्य) हर में घटाया जाना चाहिए।

उभयनिष्ठ भाजक उसी सिद्धांत के अनुसार पाया जाता है जिसका उपयोग हमने भिन्न हर वाले भिन्नों को जोड़ते समय किया था। सबसे पहले, दोनों भिन्नों के हरों का ल.स.प. ज्ञात कीजिए। फिर LCM को पहले भिन्न के हर से विभाजित किया जाता है और पहला अतिरिक्त गुणक प्राप्त होता है, जिसे पहले भिन्न के ऊपर लिखा जाता है। इसी तरह, एलसीएम को दूसरे अंश के भाजक से विभाजित किया जाता है और दूसरा अतिरिक्त कारक प्राप्त होता है, जिसे दूसरे अंश के ऊपर लिखा जाता है।

अंशों को तब उनके अतिरिक्त कारकों से गुणा किया जाता है। इन संक्रियाओं के परिणामस्वरूप, भिन्न भाजक वाले अंश समान भाजक वाले भिन्नों में बदल जाते हैं। और हम पहले से ही जानते हैं कि ऐसे अंशों को कैसे घटाना है।

उदाहरण 1व्यंजक का मान ज्ञात कीजिए:

इन भिन्नों के अलग-अलग भाजक हैं, इसलिए आपको उन्हें समान (सामान्य) हर में लाने की आवश्यकता है।

सबसे पहले, हम दोनों भिन्नों के हरों का लघुत्तम समापवर्त्य ज्ञात करते हैं। पहले भिन्न का हर संख्या 3 है, और दूसरे भिन्न का हर संख्या 4 है। इन संख्याओं का लघुत्तम समापवर्तक 12 है

एलसीएम (3 और 4) = 12

अब वापस भिन्नों पर और

आइए पहले भिन्न के लिए एक अतिरिक्त गुणनखण्ड ज्ञात करें। ऐसा करने के लिए, हम LCM को पहले भिन्न के हर से विभाजित करते हैं। LCM संख्या 12 है, और पहले भिन्न का हर 3 है। 12 को 3 से विभाजित करें, हमें 4 मिलता है। हम पहले भिन्न पर चार लिखते हैं:

हम दूसरे अंश के साथ भी ऐसा ही करते हैं। हम LCM को दूसरे भिन्न के हर से विभाजित करते हैं। लघुत्तम समापवर्त्य संख्या 12 है, और दूसरे भिन्न का हर संख्या 4 है। 12 को 4 से भाग दें, हमें 3 मिलता है। दूसरे भिन्न पर तिगुना लिखें:

अब हम घटाव के लिए पूरी तरह तैयार हैं। यह अंशों को उनके अतिरिक्त कारकों से गुणा करना बाकी है:

हम इस नतीजे पर पहुंचे कि जिन भिन्नों के हर अलग-अलग थे, वे भिन्नों में बदल गईं जिनके हर समान थे। और हम पहले से ही जानते हैं कि ऐसे अंशों को कैसे घटाना है। आइए इस उदाहरण को अंत तक पूरा करें:

उत्तर मिला

आइए चित्र का उपयोग करके हमारे समाधान को चित्रित करने का प्रयास करें। अगर आप पिज्जा से पिज्जा काटते हैं, तो आपको पिज्जा मिलता है।

यह समाधान का विस्तृत संस्करण है। स्कूल में होने के कारण, हमें इस उदाहरण को छोटे रूप में हल करना होगा। ऐसा समाधान इस तरह दिखेगा:

एक चित्र का उपयोग करके भिन्नों और एक सामान्य भाजक में कमी को भी चित्रित किया जा सकता है। इन भिन्नों को एक उभयनिष्ठ भाजक में लाने पर, हमें भिन्न और . इन भिन्नों को एक ही पिज़्ज़ा स्लाइस द्वारा दर्शाया जाएगा, लेकिन इस बार उन्हें समान भिन्नों में विभाजित किया जाएगा (समान भाजक में घटाया गया):

पहली ड्राइंग एक अंश (बारह में से आठ टुकड़े) दिखाती है, और दूसरी तस्वीर एक अंश (बारह में से तीन टुकड़े) दिखाती है। आठ टुकड़ों में से तीन टुकड़े करने पर हमें बारह में से पाँच टुकड़े मिलते हैं। अंश इन पांच टुकड़ों का वर्णन करता है।

उदाहरण 2एक व्यंजक का मान ज्ञात कीजिए

इन भिन्नों के अलग-अलग भाजक हैं, इसलिए आपको पहले उन्हें समान (सामान्य) हर में लाने की आवश्यकता है।

इन भिन्नों के हरों का लघुत्तम समापवर्त्य ज्ञात कीजिए।

अंशों के हर 10, 3 और 5 हैं। इन संख्याओं का सबसे छोटा सामान्य गुणक 30 है

ल.स.प.(10, 3, 5) = 30

अब हम प्रत्येक भिन्न के लिए अतिरिक्त गुणनखण्ड ज्ञात करते हैं। ऐसा करने के लिए, हम LCM को प्रत्येक भिन्न के हर से विभाजित करते हैं।

आइए पहले भिन्न के लिए एक अतिरिक्त गुणनखण्ड ज्ञात करें। LCM संख्या 30 है, और पहले भिन्न का हर 10 है। 30 को 10 से विभाजित करें, हमें पहला अतिरिक्त कारक 3 मिलता है। हम इसे पहले भिन्न पर लिखते हैं:

अब हम दूसरे भिन्न के लिए एक अतिरिक्त गुणनखण्ड ज्ञात करते हैं। LCM को दूसरे भिन्न के हर से विभाजित करें। लघुत्तम समापवर्तक संख्या 30 है, और दूसरे भिन्न का भाजक संख्या 3 है। 30 को 3 से विभाजित करने पर, हमें दूसरा अतिरिक्त कारक 10 मिलता है। हम इसे दूसरे भिन्न पर लिखते हैं:

अब हम तीसरे भिन्न के लिए एक अतिरिक्त गुणनखण्ड ज्ञात करते हैं। LCM को तीसरे भिन्न के हर से विभाजित करें। लघुत्तम समापवर्त्य संख्या 30 है, और तीसरे भिन्न का हर संख्या 5 है। 30 को 5 से विभाजित करने पर, हमें तीसरा अतिरिक्त कारक 6 प्राप्त होता है। हम इसे तीसरे भिन्न पर लिखते हैं:

अब घटाव के लिए सब कुछ तैयार है। यह अंशों को उनके अतिरिक्त कारकों से गुणा करना बाकी है:

हम इस निष्कर्ष पर पहुंचे कि जिन भिन्नों के हर अलग-अलग थे, वे भिन्नों में बदल गए जिनके समान (सामान्य) भाजक हैं। और हम पहले से ही जानते हैं कि ऐसे अंशों को कैसे घटाना है। आइए इस उदाहरण को समाप्त करें।

उदाहरण की निरंतरता एक पंक्ति में फिट नहीं होगी, इसलिए हम निरंतरता को अगली पंक्ति में ले जाते हैं। नई लाइन पर बराबर चिह्न (=) के बारे में मत भूलना:

उत्तर सही अंश निकला, और सब कुछ हमें सूट करता है, लेकिन यह बहुत बोझिल और बदसूरत है। हमें इसे आसान बनाना चाहिए। क्या किया जा सकता है? आप इस अंश को कम कर सकते हैं।

एक अंश को कम करने के लिए, आपको इसके अंश और भाजक को (gcd) संख्या 20 और 30 से विभाजित करना होगा।

तो, हम 20 और 30 की संख्या का जीसीडी पाते हैं:

अब हम अपने उदाहरण पर लौटते हैं और भिन्न के अंश और हर को प्राप्त GCD से विभाजित करते हैं, अर्थात 10 से

उत्तर मिला

एक अंश को एक संख्या से गुणा करना

किसी भिन्न को किसी संख्या से गुणा करने के लिए, आपको दिए गए भिन्न के अंश को इस संख्या से गुणा करना होगा और हर को वही रहने देना होगा।

उदाहरण 1. अंश को संख्या 1 से गुणा करें।

अंश के अंश को संख्या 1 से गुणा करें

प्रवेश को आधा 1 बार लेने के रूप में समझा जा सकता है। उदाहरण के लिए, यदि आप 1 बार पिज़्ज़ा लेते हैं, तो आपको पिज़्ज़ा मिलता है

गुणन के नियमों से हम जानते हैं कि यदि गुण्य और गुणक को आपस में बदल दिया जाए, तो गुणनफल नहीं बदलेगा। यदि व्यंजक को के रूप में लिखा जाता है, तो गुणनफल अभी भी के बराबर होगा। फिर से, एक पूर्णांक और एक भिन्न को गुणा करने का नियम काम करता है:

इस प्रविष्टि को इकाई का आधा हिस्सा लेने के रूप में समझा जा सकता है। उदाहरण के लिए, यदि 1 पूरा पिज़्ज़ा है और हम उसका आधा लेते हैं, तो हमारे पास पिज़्ज़ा होगा:

उदाहरण 2. एक व्यंजक का मान ज्ञात कीजिए

अंश के अंश को 4 से गुणा करें

उत्तर एक अनुचित अंश है। आइए इसका पूरा हिस्सा लें:

अभिव्यक्ति को दो तिमाहियों को 4 बार लेने के रूप में समझा जा सकता है। उदाहरण के लिए, यदि आप 4 बार पिज़्ज़ा लेते हैं, तो आपको दो पूरे पिज़्ज़ा मिलते हैं।

और यदि हम गुण्य और गुणक को स्थानों में अदला-बदली करते हैं, तो हमें व्यंजक मिलता है। यह भी 2 के बराबर होगा। इस अभिव्यक्ति को चार पूरे पिज्जा से दो पिज्जा लेने के रूप में समझा जा सकता है:

अंशों का गुणन

भिन्नों का गुणा करने के लिए, आपको उनके अंशों और हरों का गुणा करना होगा। यदि उत्तर एक अनुचित अंश है, तो आपको इसमें पूरे भाग का चयन करना होगा।

उदाहरण 1व्यंजक का मान ज्ञात कीजिए।

उत्तर मिला। इस अंश को कम करना वांछनीय है। अंश को 2 से कम किया जा सकता है। फिर अंतिम समाधान निम्न रूप लेगा:

अभिव्यक्ति को आधे पिज्जा से पिज्जा लेने के रूप में समझा जा सकता है। मान लें कि हमारे पास आधा पिज़्ज़ा है:

इस आधे से दो तिहाई कैसे लें? पहले आपको इस आधे हिस्से को तीन बराबर भागों में बांटना होगा:

और इन तीन टुकड़ों में से दो लो:

हम पिज़्ज़ा लेंगे। याद रखें कि एक पिज़्ज़ा कैसा दिखता है जिसे तीन भागों में विभाजित किया गया है:

इस पिज़्ज़ा के एक स्लाइस और हमारे द्वारा लिए गए दो स्लाइस के आयाम समान होंगे:

दूसरे शब्दों में हम उसी पिज्जा साइज की बात कर रहे हैं। इसलिए, अभिव्यक्ति का मूल्य है

उदाहरण 2. एक व्यंजक का मान ज्ञात कीजिए

पहले भिन्न के अंश को दूसरे भिन्न के अंश से और पहले भिन्न के हर को दूसरे भिन्न के हर से गुणा करें:

उत्तर एक अनुचित अंश है। आइए इसका पूरा हिस्सा लें:

उदाहरण 3एक व्यंजक का मान ज्ञात कीजिए

उत्तर सही अंश निकला, लेकिन इसे कम कर दिया जाए तो अच्छा होगा। इस अंश को कम करने के लिए, आपको इस अंश के अंश और भाजक को सबसे बड़े से विभाजित करना होगा सामान्य विभाजक(gcd) संख्या 105 और 450।

तो, आइए 105 और 450 की संख्या का GCD ज्ञात करें:

अब हम अपने उत्तर के अंश और हर को जीसीडी में विभाजित करते हैं जो हमने पाया है, अर्थात 15 से

पूर्णांक को भिन्न के रूप में निरूपित करना

किसी भी पूर्ण संख्या को भिन्न के रूप में दर्शाया जा सकता है। उदाहरण के लिए, संख्या 5 को के रूप में दर्शाया जा सकता है। इससे, पाँच का अर्थ नहीं बदलेगा, क्योंकि अभिव्यक्ति का अर्थ है "संख्या पाँच एक से विभाजित", और यह, जैसा कि आप जानते हैं, पाँच के बराबर है:

उलटा अंक

अब हम परिचित होंगे दिलचस्प विषयगणित में। इसे "रिवर्स नंबर" कहा जाता है।

परिभाषा। संख्या के विपरीतए वह संख्या है, जिससे गुणा करने परए एक इकाई देता है।

आइए इस परिभाषा में एक चर के बजाय स्थानापन्न करें एसंख्या 5 और परिभाषा पढ़ने का प्रयास करें:

संख्या के विपरीत 5 वह संख्या है, जिससे गुणा करने पर 5 एक इकाई देता है।

क्या कोई ऐसी संख्या ज्ञात करना संभव है जिसे 5 से गुणा करने पर एक प्राप्त हो? यह पता चला है कि आप कर सकते हैं। आइए पांच को एक अंश के रूप में दर्शाते हैं:

फिर इस अंश को उसी से गुणा करें, बस अंश और हर को अदल-बदल कर दें। दूसरे शब्दों में, आइए अंश को उसी से गुणा करें, केवल उलटा:

इसका परिणाम क्या होगा? यदि हम इस उदाहरण को हल करना जारी रखते हैं, तो हमें एक मिलता है:

इसका मतलब यह है कि संख्या 5 का प्रतिलोम संख्या है, क्योंकि जब 5 को एक से गुणा किया जाता है, तो एक प्राप्त होता है।

व्युत्क्रम किसी अन्य पूर्णांक के लिए भी पाया जा सकता है।

आप किसी अन्य भिन्न का व्युत्क्रम भी ज्ञात कर सकते हैं। ऐसा करने के लिए, इसे चालू करने के लिए पर्याप्त है।

एक अंश का एक संख्या से विभाजन

मान लें कि हमारे पास आधा पिज़्ज़ा है:

आइए इसे दो के बीच समान रूप से विभाजित करें। प्रत्येक को कितने पिज्जा मिलेंगे?

यह देखा जा सकता है कि आधे पिज़्ज़ा को विभाजित करने के बाद, दो बराबर टुकड़े प्राप्त हुए, जिनमें से प्रत्येक से एक पिज़्ज़ा बनता है। इसलिए सभी को पिज्जा मिलता है।

भिन्नों का विभाजन व्युत्क्रमों का उपयोग करके किया जाता है। व्युत्क्रम आपको विभाजन को गुणन से बदलने की अनुमति देता है।

किसी अंश को किसी संख्या से विभाजित करने के लिए, आपको इस भिन्न को भाजक के व्युत्क्रम से गुणा करना होगा।

इस नियम का उपयोग करते हुए, हम अपने आधे पिज़्ज़ा के विभाजन को दो भागों में लिखेंगे।

तो, आपको अंश को संख्या 2 से विभाजित करने की आवश्यकता है। यहाँ भाज्य एक भिन्न है और भाजक 2 है।

किसी भिन्न को संख्या 2 से विभाजित करने के लिए, आपको इस भिन्न को भाजक 2 के व्युत्क्रम से गुणा करना होगा। भाजक 2 का व्युत्क्रम एक भिन्न है। इसलिए आपको गुणा करना होगा

गुणन और अंशों का विभाजन।

ध्यान!
अतिरिक्त हैं
विशेष धारा 555 में सामग्री।
उन लोगों के लिए जो दृढ़ता से "बहुत नहीं ..."
और उनके लिए जो "बहुत अधिक ...")

उदाहरण के लिए:

पहले मामले में (बाईं ओर अभिव्यक्ति):

दूसरे में (दाईं ओर अभिव्यक्ति):

फर्क महसूस करो? 4 और 1/9!

फिर विभाजित-गुणा करें क्रम में, बाएं से दाएं!

अंशों के साथ यही सभी क्रियाएं हैं। बात काफी सरल है, लेकिन पर्याप्त से अधिक त्रुटियाँ देता है। व्यावहारिक सलाह पर ध्यान दें, और उनमें से कम (गलतियाँ) होंगी!

व्यावहारिक सुझाव:

2. विभिन्न प्रकार के अंशों वाले उदाहरणों में - साधारण भिन्नों पर जाएँ।

3. हम सभी भिन्नों को अंत तक कम करते हैं।

5. हम अपने दिमाग में इकाई को एक अंश में विभाजित करते हैं, केवल भिन्न को उलट कर।

गणना करें:

क्या आपने तय किया?

अपने से मेल खाने वाले उत्तरों की तलाश में। मैंने विशेष रूप से उन्हें एक गड़बड़ में लिखा था, प्रलोभन से दूर, बोलने के लिए ... यहाँ वे उत्तर हैं, अर्धविराम के साथ लिखे गए हैं।

0; 17/22; 3/4; 2/5; 1; 25.

और अब हम निष्कर्ष निकालते हैं। अगर सब कुछ काम कर गया - आपके लिए खुश! अंशों के साथ प्रारंभिक गणना आपकी समस्या नहीं है! आप अधिक गंभीर कार्य कर सकते हैं। अगर नहीं...

तो आपको दो में से एक समस्या है। या दोनों एक साथ।) ज्ञान की कमी और (या) असावधानी। लेकिन इस व्याख्या करने योग्य समस्या।

अगर आपको यह साइट पसंद है...

वैसे, मेरे पास आपके लिए कुछ और दिलचस्प साइटें हैं।)

आप उदाहरणों को हल करने का अभ्यास कर सकते हैं और अपने स्तर का पता लगा सकते हैं। तत्काल सत्यापन के साथ परीक्षण। सीखना - रुचि के साथ!)

आप कार्यों और डेरिवेटिव से परिचित हो सकते हैं।

पिछली बार हमने भिन्नों को जोड़ना और घटाना सीखा था (पाठ "भिन्नों का जोड़ और घटाव" देखें)। उन क्रियाओं में सबसे कठिन क्षण भिन्नों को एक आम भाजक में लाना था।

अब गुणा और भाग से निपटने का समय आ गया है। अच्छी खबर यह है कि ये ऑपरेशन जोड़ और घटाव से भी आसान हैं। आरंभ करने के लिए, सबसे सरल मामले पर विचार करें, जब एक विशिष्ट पूर्णांक भाग के बिना दो सकारात्मक भिन्न होते हैं।

दो भिन्नों का गुणा करने के लिए, आपको उनके अंशों और हरों को अलग-अलग गुणा करना होगा। पहली संख्या नए अंश का अंश होगी, और दूसरी संख्या भाजक होगी।

दो अंशों को विभाजित करने के लिए, आपको पहले अंश को "उल्टे" दूसरे से गुणा करना होगा।

पद का नाम:

परिभाषा के अनुसार हमारे पास है:

एक पूर्णांक भाग और नकारात्मक अंशों के साथ अंशों का गुणन

प्लस बार माइनस माइनस देता है;
दो नकारात्मक एक सकारात्मक बनाते हैं।

जब तक वे पूरी तरह से गायब नहीं हो जाते, तब तक हम जोड़े में माइनस को पार करते हैं। एक चरम मामले में, एक ऋण जीवित रह सकता है - वह जो एक मैच नहीं मिला;
यदि कोई माइनस नहीं बचा है, तो ऑपरेशन पूरा हो गया है - आप गुणा करना शुरू कर सकते हैं। यदि अंतिम माइनस को पार नहीं किया गया है, क्योंकि उसे एक जोड़ी नहीं मिली, हम इसे गुणन की सीमा से बाहर कर देते हैं। आपको एक नकारात्मक अंश मिलता है।

काम। व्यंजक का मान ज्ञात कीजिए:

हम सभी अंशों को अनुचित में अनुवादित करते हैं, और फिर हम गुणन की सीमा से बाहर के ऋणों को निकालते हैं। जो बचता है उसे सामान्य नियमों के अनुसार गुणा किया जाता है। हम पाते हैं:

मक्खी पर अंशों को कम करना

काम। व्यंजक का मान ज्ञात कीजिए:

परिभाषा के अनुसार हमारे पास है:

कृपया ध्यान दें: पहले मामले में, गुणक पूरी तरह से कम हो गए थे। इकाइयाँ अपने स्थान पर बनी रहीं, जिन्हें सामान्यतया छोड़ा जा सकता है। दूसरे उदाहरण में, पूर्ण कमी हासिल करना संभव नहीं था, लेकिन गणना की कुल राशि अभी भी घट गई।

आप ऐसा नहीं कर सकते!

त्रुटि इस तथ्य के कारण होती है कि अंश जोड़ते समय, योग भिन्न के अंश में दिखाई देता है, न कि संख्याओं के गुणनफल में। इसलिए, एक अंश की मुख्य संपत्ति को लागू करना असंभव है, क्योंकि यह संपत्ति विशेष रूप से संख्याओं के गुणन से संबंधित है।