Hvordan løse systemer med lineære ligninger. Ligningssystemer med to variabler, løsningsmetoder

La oss først huske definisjonen av en løsning til et ligningssystem med to variabler.

Definisjon 1

Et tallpar kalles en løsning på et likningssystem i to variabler hvis å erstatte dem i ligningen resulterer i en sann likhet.

I fremtiden vil vi vurdere systemer med to ligninger med to variabler.

Eksistere fire grunnleggende måter å løse ligningssystemer på: substitusjonsmetode, addisjonsmetode, grafisk metode, metode for å opprettholde nye variabler. La oss se på disse metodene spesifikke eksempler. For å beskrive prinsippet om å bruke de tre første metodene, vil vi vurdere et system med to lineære ligninger med to ukjente:

Substitusjonsmetode

Substitusjonsmetoden er som følger: ta hvilken som helst av disse ligningene og uttrykk $y$ i form av $x$, deretter erstattes $y$ inn i systemligningen, hvorfra variabelen $x finnes.$ Etter dette kan vi enkelt beregne variabelen $y.$

Eksempel 1

La oss uttrykke $y$ fra den andre ligningen i form av $x$:

La oss bytte inn i den første ligningen og finne $x$:

\ \ \

La oss finne $y$:

Svar: $(-2,\ 3)$

Tilleggsmetode.

La oss se på denne metoden ved å bruke et eksempel:

Eksempel 2

\[\venstre\( \begin(array)(c) (2x+3y=5) \\ (3x-y=-9) \end(array) \right.\]

Ved å multiplisere den andre ligningen med 3 får vi:

\[\venstre\( \begin(array)(c) (2x+3y=5) \\ (9x-3y=-27) \end(array) \right.\]

La oss nå legge begge ligningene sammen:

\ \ \

La oss finne $y$ fra den andre ligningen:

\[-6-y=-9\] \

Svar: $(-2,\ 3)$

Merknad 1

Merk at i denne metoden er det nødvendig å multiplisere en eller begge ligningene med slike tall at en av variablene "forsvinner".

Grafisk metode

Den grafiske metoden er som følger: begge likningene til systemet er avbildet på koordinatplanet og skjæringspunktet deres er funnet.

Eksempel 3

\[\venstre\( \begin(array)(c) (2x+3y=5) \\ (3x-y=-9) \end(array) \right.\]

La oss uttrykke $y$ fra begge ligningene i form av $x$:

\[\venstre\( \begin(array)(c) (y=\frac(5-2x)(3)) \\ (y=3x+9) \end(array) \right.\]

La oss skildre begge grafene på samme plan:

Bilde 1.

Svar: $(-2,\ 3)$

Metode for å introdusere nye variabler

La oss se på denne metoden ved å bruke følgende eksempel:

Eksempel 4

\[\venstre\( \begin(array)(c) (2^(x+1)-3^y=-1) \\ (3^y-2^x=2) \end(array) \right .\]

Løsning.

Dette systemet tilsvarer systemet

\[\venstre\( \begin(array)(c) ((2\cdot 2)^x-3^y=-1) \\ (3^y-2^x=2) \end(array) \ Ikke sant.\]

La $2^x=u\ (u>0)$ og $3^y=v\ (v>0)$, vi får:

\[\venstre\( \begin(array)(c) (2u-v=-1) \\ (v-u=2) \end(array) \right.\]

La oss løse det resulterende systemet ved å bruke addisjonsmetoden. La oss legge sammen ligningene:

\ \

Så fra den andre ligningen får vi det

Tilbake til erstatteren, får vi nytt system eksponentialligninger:

\[\venstre\( \begin(array)(c) (2^x=1) \\ (3^y=3) \end(array) \right.\]

Vi får:

\[\venstre\( \begin(array)(c) (x=0) \\ (y=1) \end(array) \right.\]

Bruksanvisning

Tilleggsmetode.
Du må skrive to strengt under hverandre:

549+45y+4y=-7, 45y+4y=549-7, 49y=542, y=542:49, y≈11.
I en vilkårlig valgt (fra systemet) ligning, sett inn tallet 11 i stedet for det allerede funnet "spillet" og beregn det andre ukjente:

X=61+5*11, x=61+55, x=116.
Svaret på dette ligningssystemet er x=116, y=11.

Grafisk metode.
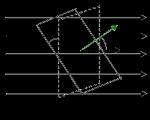
Den består i å praktisk talt finne koordinatene til punktet der linjene er matematisk skrevet i et ligningssystem. Grafene til begge linjene skal tegnes separat i samme koordinatsystem. Generell oversikt: – y=khx+b. For å konstruere en rett linje er det nok å finne koordinatene til to punkter, og x velges vilkårlig.
La systemet være gitt: 2x – y=4

Y=-3x+1.
En rett linje er konstruert ved å bruke den første, for enkelhets skyld bør den skrives ned: y=2x-4. Kom opp med (enklere) verdier for x, bytt den inn i ligningen, løs den og finn y. Vi får to punkter som en rett linje er konstruert langs. (se bilde)
x 0 1

y -4 -2
En rett linje er konstruert ved å bruke den andre ligningen: y=-3x+1.
Konstruer også en rett linje. (se bilde)

y 1 -5
Finn koordinatene til skjæringspunktet til to konstruerte linjer på grafen (hvis linjene ikke skjærer hverandre, så har ikke ligningssystemet - så).

Video om emnet

Nyttige råd

Hvis det samme likningssystemet løses med tre forskjellige måter, vil svaret være det samme (hvis løsningen er riktig).

Kilder:

• 8. klasse algebra
• løse en ligning med to ukjente på nettet
• Eksempler på å løse systemer av lineære ligninger med to

System ligninger er en samling matematiske poster, som hver inneholder en rekke variabler. Det er flere måter å løse dem på.

Du vil trenge

• -Linjal og blyant;
• -kalkulator.

Bruksanvisning

La oss vurdere sekvensen for å løse systemet, som består av lineære ligninger med formen: a1x + b1y = c1 og a2x + b2y = c2. Hvor x og y er ukjente variabler, og b,c er frie ledd. Når du bruker denne metoden, representerer hvert system koordinatene til punktene som tilsvarer hver ligning. For å begynne, i hvert tilfelle, uttrykk en variabel i form av en annen. Sett deretter variabelen x til et hvilket som helst antall verdier. To er nok. Bytt inn i ligningen og finn y. Konstruer et koordinatsystem, merk de resulterende punktene på det og tegn en linje gjennom dem. Tilsvarende beregninger må utføres for andre deler av systemet.

Systemet har en unik løsning dersom de konstruerte linjene krysser hverandre og en felles poeng. Det er uforenlig hvis de er parallelle med hverandre. Og den har uendelig mange løsninger når linjene smelter sammen.

Denne metoden anses som veldig visuell. Den største ulempen er at de beregnede ukjente har omtrentlige verdier. Mer nøyaktige resultater er gitt av de såkalte algebraiske metodene.

Enhver løsning på et ligningssystem er verdt å sjekke. For å gjøre dette, erstatte de resulterende verdiene i stedet for variablene. Du kan også finne løsningen ved hjelp av flere metoder. Hvis løsningen av systemet er riktig, bør alle vise seg like.

Ofte er det ligninger der ett av begrepene er ukjent. For å løse en ligning må du huske og utføre et bestemt sett med handlinger med disse tallene.

Du vil trenge

• - papir;
• - penn eller blyant.

Bruksanvisning

Tenk deg at det er 8 kaniner foran deg, og du har bare 5 gulrøtter. Tenk på det, du må fortsatt kjøpe flere gulrøtter slik at hver kanin får en.

La oss presentere dette problemet i form av en ligning: 5 + x = 8. La oss erstatte tallet 3 i stedet for x. Faktisk, 5 + 3 = 8.

Når du erstattet x med et tall, gjorde du det samme som da du trakk 5 fra 8. Så for å finne ukjent ledd, trekk det kjente leddet fra summen.

La oss si at du har 20 kaniner og bare 5 gulrøtter. La oss finne på det. En ligning er en likhet som bare gjelder for visse verdier av bokstavene som er inkludert i den. Bokstavene hvis betydning må finnes, kalles . Skriv en likning med en ukjent, kall den x. Når vi løser kaninproblemet vårt, får vi følgende ligning: 5 + x = 20.

La oss finne forskjellen mellom 20 og 5. Når du trekker fra, er tallet som det trekkes fra det som reduseres. Tallet som trekkes fra kalles , og det endelige resultatet kalles differansen. Så, x = 20 – 5; x = 15. Du må kjøpe 15 gulrøtter til kaninene.

Sjekk: 5 + 15 = 20. Ligningen er løst riktig. Selvfølgelig, når vi snakker om om slike enkle er det ikke nødvendig å utføre en sjekk. Men når du har ligninger med tresifrede, firesifrede osv. tall, må du definitivt sjekke for å være helt sikker på resultatet av arbeidet ditt.

Video om emnet

Nyttige råd

For å finne den ukjente minuenden, må du legge til subtrahenden til forskjellen.

For å finne den ukjente subtrahenden, må du trekke forskjellen fra minuenden.

Tips 4: Hvordan løse et system med tre ligninger med tre ukjente

Et system med tre ligninger med tre ukjente har kanskje ikke løsninger, til tross for et tilstrekkelig antall ligninger. Du kan prøve å løse det ved å bruke substitusjonsmetoden eller ved å bruke Cramers metode. Cramers metode, i tillegg til å løse systemet, lar deg vurdere om systemet er løsbart før du finner verdiene til de ukjente.

Bruksanvisning

Substitusjonsmetoden består av sekvensielt sekvensielt en ukjent gjennom to andre og erstatte det resulterende resultatet i systemets ligninger. La et system med tre ligninger gis i generell form:

a1x + b1y + c1z = d1

a2x + b2y + c2z = d2

a3x + b3y + c3z = d3

Uttrykk x fra den første ligningen: x = (d1 - b1y - c1z)/a1 - og bytt inn i den andre og tredje ligningen, uttryk deretter y fra den andre ligningen og bytt inn i den tredje. Du får et lineært uttrykk for z gjennom koeffisientene til systemlikningene. Gå nå "bakover": bytt inn z i den andre ligningen og finn y, og bytt deretter ut z og y i den første og løs for x. Prosessen er generelt vist i figuren før du finner z. Videre skriving i generell form vil være for tungvint; i praksis, ved å erstatte , kan du ganske enkelt finne alle tre ukjente.

Cramers metode består i å konstruere en systemmatrise og beregne determinanten til denne matrisen, samt ytterligere tre hjelpematriser. Systemmatrisen er sammensatt av koeffisienter for de ukjente leddene i ligningene. En kolonne som inneholder tallene på høyre side av ligninger, en kolonne med høyre sider. Det brukes ikke i systemet, men brukes ved løsning av systemet.

Video om emnet

Merk

Alle ligninger i systemet skal gi tilleggsinformasjon uavhengig av andre ligninger. Ellers vil systemet være underbestemt og det vil ikke være mulig å finne en entydig løsning.

Nyttige råd

Etter å ha løst ligningssystemet, bytter du de funnet verdiene inn i det opprinnelige systemet og kontrollerer at de tilfredsstiller alle ligningene.

Av seg selv ligningen med tre ukjent har mange løsninger, så som oftest er det supplert med ytterligere to likninger eller betingelser. Avhengig av hva de første dataene er, vil forløpet av beslutningen i stor grad avhenge.

Du vil trenge

• - et system med tre ligninger med tre ukjente.

Bruksanvisning

Hvis to av de tre systemene bare har to av de tre ukjente, prøv å uttrykke noen variabler i form av de andre og erstatte dem med ligningen med tre ukjent. Målet ditt i dette tilfellet er å gjøre det til normalt ligningen med en ukjent person. Hvis dette er , er den videre løsningen ganske enkel - bytt den funnet verdien inn i andre ligninger og finn alle de andre ukjente.

Noen ligningssystemer kan trekkes fra en ligning med en annen. Se om det er mulig å multiplisere en av eller en variabel slik at to ukjente blir kansellert på en gang. Hvis det er en slik mulighet, dra nytte av den; mest sannsynlig vil den påfølgende løsningen ikke være vanskelig. Husk at når du multipliserer med et tall, må du gange både venstre og høyre side. På samme måte, når du trekker fra ligninger, må du huske at høyre side også må trekkes fra.

Hvis tidligere metoder hjalp ikke, bruk den generelle metoden for å løse eventuelle ligninger med tre ukjent. For å gjøre dette, omskriv likningene i formen a11x1+a12x2+a13x3=b1, a21x1+a22x2+a23x3=b2, a31x1+a32x2+a33x3=b3. Lag nå en matrise med koeffisienter for x (A), en matrise med ukjente (X) og en matrise med frie variabler (B). Vær oppmerksom på at ved å multiplisere matrisen av koeffisienter med matrisen av ukjente, vil du få en matrise av frie ledd, det vil si A*X=B.

Finn matrise A i potensen (-1) ved først å finne , merk at den ikke skal være lik null. Etter dette, multipliser den resulterende matrisen med matrise B, som et resultat vil du motta den ønskede matrisen X, som indikerer alle verdiene.

Du kan også finne en løsning på et system med tre ligninger ved hjelp av Cramers metode. For å gjøre dette, finn tredjeordens determinanten ∆ som tilsvarer systemmatrisen. Finn deretter tre flere determinanter ∆1, ∆2 og ∆3 suksessivt, og bytt ut verdiene til de frie leddene i stedet for verdiene til de tilsvarende kolonnene. Finn nå x: x1=∆1/∆, x2=∆2/∆, x3=∆3/∆.

Kilder:

• løsninger på ligninger med tre ukjente

Når du begynner å løse et ligningssystem, finn ut hva slags ligninger de er. Metoder for å løse lineære ligninger har blitt studert ganske godt. Ikke-lineære ligninger løses oftest ikke. Det er bare ett spesialtilfelle, som hver er praktisk talt individuell. Derfor bør studiet av løsningsteknikker begynne med lineære ligninger. Slike ligninger kan til og med løses rent algoritmisk.

nevnerne til de ukjente funnet er nøyaktig de samme. Ja, og tellerne viser noen mønstre i konstruksjonen deres. Hvis dimensjonen til ligningssystemet var større enn to, ville eliminasjonsmetoden ført til svært tungvinte beregninger. For å unngå dem er det utviklet rene algoritmiske løsninger. Den enkleste av dem er Cramers algoritme (Cramers formler). For det burde du finne ut av generelt system ligninger fra n ligninger.

Et system med n lineære algebraiske ligninger med n ukjente har formen (se fig. 1a). I den er аij koeffisientene til systemet,
xj – ukjente, bi – frie termer (i=1, 2, ... , n; j=1, 2, ... , n). Et slikt system kan skrives kompakt i matriseform AX=B. Her er A matrisen av systemkoeffisienter, X er kolonnematrisen av ukjente, B er kolonnematrisen av frie ledd (se figur 1b). I følge Cramers metode er hver ukjent xi =∆i/∆ (i=1,2…,n). Determinanten ∆ til koeffisientmatrisen kalles hoved, og ∆i hjelpematrisen. For hver ukjent blir hjelpedeterminanten funnet ved å erstatte den i-te kolonnen i hoveddeterminanten med en kolonne med frie termer. Cramer-metoden for andre- og tredjeordens systemer er presentert i detalj i fig. 2.

Systemet er en kombinasjon av to eller flere likheter, som hver inneholder to eller flere ukjente. Det er to hovedmåter å løse systemer med lineære ligninger som brukes innenfor skolepensum. En av dem kalles metoden, den andre - addisjonsmetoden.

Standardform av et system med to ligninger

På standard skjema den første ligningen har formen a1*x+b1*y=c1, den andre ligningen har formen a2*x+b2*y=c2 og så videre. For eksempel, i tilfelle av to deler av systemet, er begge gitt a1, a2, b1, b2, c1, c2 noen numeriske koeffisienter representert i spesifikke ligninger. I sin tur representerer x og y ukjente hvis verdier må bestemmes. De nødvendige verdiene gjør begge ligningene samtidig til sanne likheter.

Løse systemet ved hjelp av addisjonsmetoden

For å løse systemet, det vil si å finne de verdiene av x og y som vil gjøre dem til sanne likheter, må du ta flere enkle trinn. Den første av dem er å transformere en av ligningene slik at de numeriske koeffisientene for variabelen x eller y i begge ligningene er like i størrelse, men forskjellige i fortegn.

Anta for eksempel at det er gitt et system som består av to ligninger. Den første av dem har formen 2x+4y=8, den andre har formen 6x+2y=6. Et av alternativene for å fullføre oppgaven er å multiplisere den andre ligningen med en koeffisient på -2, som vil føre den til formen -12x-4y=-12. Riktig valg av koeffisient er en av nøkkeloppgavene i prosessen med å løse et system ved hjelp av addisjonsmetoden, siden det bestemmer hele det videre forløpet av prosedyren for å finne ukjente.

Nå er det nødvendig å legge til de to likningene til systemet. Åpenbart vil gjensidig ødeleggelse av variabler med koeffisienter like i verdi, men motsatt i fortegn, føre til formen -10x=-4. Etter dette er det nødvendig å løse denne enkle ligningen, hvorfra det tydelig følger at x = 0,4.

Det siste trinnet i løsningsprosessen er substitusjonen av funnverdien til en av variablene i en av de initiale likhetene som er tilgjengelige i systemet. Hvis du for eksempel erstatter x=0,4 i den første ligningen, kan du få uttrykket 2*0,4+4y=8, hvorfra y=1,8. Dermed er x=0,4 og y=1,8 røttene til eksempelsystemet.

For å sikre at røttene ble funnet riktig, er det nyttig å sjekke ved å erstatte de funnet verdiene i den andre ligningen i systemet. For eksempel i i dette tilfellet vi får en likhet på formen 0,4*6+1,8*2=6, som er sant.

Video om emnet

Løse systemer av lineære algebraiske ligninger (SLAE) er utvilsomt det viktigste temaet i et lineært algebrakurs. Et stort antall problemer fra alle grener av matematikken kommer ned til å løse systemer av lineære ligninger. Disse faktorene forklarer årsaken til denne artikkelen. Materialet til artikkelen er valgt og strukturert slik at du med dens hjelp kan

• velg den optimale metoden for å løse systemet med lineære algebraiske ligninger,
• studere teorien om den valgte metoden,
• løse systemet med lineære ligninger ved å vurdere detaljerte løsninger på typiske eksempler og problemer.

Kort beskrivelse av artikkelmaterialet.

Først gir vi alle nødvendige definisjoner, begreper og introduserer notasjoner.

Deretter vil vi vurdere metoder for å løse systemer av lineære algebraiske ligninger der antall ligninger er lik antall ukjente variabler og som har en unik løsning. For det første vil vi fokusere på Cramers metode, for det andre vil vi vise matrisemetoden for å løse slike ligningssystemer, og for det tredje vil vi analysere Gauss-metoden (metoden for sekvensiell eliminering av ukjente variabler). For å konsolidere teorien vil vi definitivt løse flere SLAE-er på forskjellige måter.

Etter dette vil vi gå videre til å løse systemer med lineære algebraiske ligninger generelt syn, der antall ligninger ikke sammenfaller med antall ukjente variabler eller hovedmatrisen til systemet er entall. La oss formulere Kronecker-Capelli-teoremet, som lar oss etablere kompatibiliteten til SLAE-er. La oss analysere løsningen av systemer (hvis de er kompatible) ved å bruke konseptet med en basis-minor av en matrise. Vi vil også vurdere Gauss-metoden og beskrive i detalj løsningene på eksemplene.

Vi vil definitivt dvele ved strukturen til den generelle løsningen av homogene og inhomogene systemer av lineære algebraiske ligninger. La oss gi konseptet med et grunnleggende system av løsninger og vise hvordan den generelle løsningen til en SLAE er skrevet ved å bruke vektorene til det grunnleggende løsningssystemet. For en bedre forståelse, la oss se på noen få eksempler.

Avslutningsvis vil vi vurdere likningssystemer som kan reduseres til lineære, samt ulike problemer i løsningen av hvilke SLAE-er oppstår.

Sidenavigering.

Definisjoner, begreper, betegnelser.

Vi vil vurdere systemer med p lineære algebraiske ligninger med n ukjente variabler (p kan være lik n) av formen

Ukjente variabler, - koeffisienter (noen reelle eller komplekse tall), - frie ledd (også reelle eller komplekse tall).

Denne formen for opptak SLAE kalles koordinere.

I matriseformå skrive dette ligningssystemet har formen,
Hvor - systemets hovedmatrise, - en kolonnematrise med ukjente variabler, - en kolonnematrise med frie ledd.

Legger vi til en matrisekolonne med frie ledd til matrise A som (n+1)te kolonne, får vi den s.k. utvidet matrise systemer av lineære ligninger. Vanligvis er den utvidede matrisen merket med bokstaven T, og kolonnen med frie termer er skilt vertikal linje fra de resterende kolonnene, det vil si

Løse et system med lineære algebraiske ligninger kalt et sett med verdier av ukjente variabler som gjør alle likninger i systemet til identiteter. Matriseligningen for gitte verdier av de ukjente variablene blir også en identitet.

Hvis et ligningssystem har minst én løsning, kalles det ledd.

Hvis et ligningssystem ikke har noen løsninger, kalles det ikke-ledd.

Hvis en SLAE har en unik løsning, kalles den sikker; hvis det er mer enn én løsning, så – usikker.

Hvis de frie leddene til alle likningene i systemet er lik null , så kalles systemet homogen, ellers - heterogen.

Løse elementære systemer av lineære algebraiske ligninger.

Hvis antallet ligninger i et system er lik antall ukjente variabler og determinanten til hovedmatrisen ikke er lik null, vil slike SLAE-er bli kalt elementær. Slike ligningssystemer har en unik løsning, og ved et homogent system er alle ukjente variabler lik null.

Vi begynte å studere slike SLAE-er i videregående skole. Når vi løste dem, tok vi en likning, uttrykte en ukjent variabel i form av andre og erstattet den i de resterende likningene, tok deretter den neste likningen, uttrykte den neste ukjente variabelen og erstattet den i andre likninger, og så videre. Eller de brukte addisjonsmetoden, det vil si at de la til to eller flere ligninger for å eliminere noen ukjente variabler. Vi vil ikke dvele ved disse metodene i detalj, siden de i hovedsak er modifikasjoner av Gauss-metoden.

Hovedmetodene for å løse elementære systemer av lineære ligninger er Cramer-metoden, matrisemetoden og Gauss-metoden. La oss sortere dem.

Løse systemer av lineære ligninger ved hjelp av Cramers metode.

Anta at vi må løse et system med lineære algebraiske ligninger

hvor antall ligninger er lik antall ukjente variabler og determinanten til hovedmatrisen til systemet er forskjellig fra null, det vil si .

La være determinanten for hovedmatrisen til systemet, og - determinanter av matriser som er hentet fra A ved erstatning 1., 2., …, n kolonnen til kolonnen med gratis medlemmer:

Med denne notasjonen beregnes ukjente variabler ved å bruke formlene til Cramers metode som . Slik finner man løsningen på et system med lineære algebraiske ligninger ved hjelp av Cramers metode.

Eksempel.

Cramers metode .

Løsning.

Hovedmatrisen til systemet har formen . La oss beregne dens determinant (om nødvendig, se artikkelen):

Siden determinanten for hovedmatrisen til systemet ikke er null, har systemet en unik løsning som kan bli funnet med Cramers metode.

La oss komponere og beregne de nødvendige determinantene (vi får determinanten ved å erstatte den første kolonnen i matrise A med en kolonne med frie termer, determinanten ved å erstatte den andre kolonnen med en kolonne med frie termer, og ved å erstatte den tredje kolonnen i matrise A med en kolonne med frie termer) :

Finne ukjente variabler ved hjelp av formler :

Svar:

Den største ulempen med Cramers metode (hvis den kan kalles en ulempe) er kompleksiteten ved å beregne determinanter når antallet ligninger i systemet er mer enn tre.

Løse systemer av lineære algebraiske ligninger ved hjelp av matrisemetoden (ved å bruke en invers matrise).

La et system med lineære algebraiske ligninger gis i matriseform, der matrisen A har dimensjon n med n og dens determinant er ikke null.

Siden , matrise A er inverterbar, det vil si at det er en invers matrise. Hvis vi multipliserer begge sider av likheten med venstre, får vi en formel for å finne en matrisekolonne med ukjente variabler. Slik fikk vi en løsning på et system av lineære algebraiske ligninger ved hjelp av matrisemetoden.

Eksempel.

Løs system av lineære ligninger matrisemetoden.

Løsning.

La oss omskrive ligningssystemet i matriseform:

Fordi

så kan SLAE løses ved hjelp av matrisemetoden. Ved å bruke den inverse matrisen kan løsningen på dette systemet finnes som .

La oss konstruere en invers matrise ved å bruke en matrise fra algebraiske addisjoner av elementer i matrise A (om nødvendig, se artikkelen):

Det gjenstår å beregne matrisen av ukjente variabler ved å multiplisere den inverse matrisen til en matrisekolonne med gratis medlemmer (om nødvendig, se artikkelen):

Svar:

eller i en annen notasjon x 1 = 4, x 2 = 0, x 3 = -1.

Hovedproblemet når man finner løsninger på systemer med lineære algebraiske ligninger ved bruk av matrisemetoden, er kompleksiteten ved å finne den inverse matrisen, spesielt for kvadratiske matriser av orden høyere enn tredje.

Løse systemer av lineære ligninger ved hjelp av Gauss-metoden.

Anta at vi må finne en løsning på et system med n lineære ligninger med n ukjente variabler
determinanten til hovedmatrisen som er forskjellig fra null.

Essensen av Gauss-metoden består av sekvensiell ekskludering av ukjente variabler: først ekskluderes x 1 fra alle likninger i systemet, starter fra den andre, deretter ekskluderes x 2 fra alle ligninger, starter fra den tredje, og så videre, inntil bare den ukjente variabelen x n forblir i den siste ligningen. Denne prosessen med å transformere systemligninger for å sekvensielt eliminere ukjente variabler kalles direkte gaussisk metode. Etter å ha fullført foroverslaget til Gauss-metoden, blir x n funnet fra den siste ligningen, ved å bruke denne verdien fra den nest siste ligningen, beregnes x n-1, og så videre, x 1 blir funnet fra den første ligningen. Prosessen med å beregne ukjente variabler når man går fra den siste ligningen i systemet til den første kalles invers av Gauss-metoden.

La oss kort beskrive algoritmen for å eliminere ukjente variabler.

Vi vil anta det, siden vi alltid kan oppnå dette ved å omorganisere likningene til systemet. La oss eliminere den ukjente variabelen x 1 fra alle likninger i systemet, og starter med den andre. For å gjøre dette, til den andre ligningen i systemet legger vi den første, multiplisert med , til den tredje ligningen legger vi den første, multiplisert med , og så videre, til den n-te ligningen legger vi den første, multiplisert med . Ligningssystemet etter slike transformasjoner vil ta formen

hvor og .

Vi ville ha kommet til det samme resultatet hvis vi hadde uttrykt x 1 i form av andre ukjente variabler i den første likningen av systemet og erstattet det resulterende uttrykket i alle andre likninger. Dermed er variabelen x 1 ekskludert fra alle ligninger, fra den andre.

Deretter fortsetter vi på lignende måte, men bare med en del av det resulterende systemet, som er markert i figuren

For å gjøre dette legger vi til den tredje likningen i systemet den andre, multiplisert med , til den fjerde likningen legger vi den andre, multiplisert med , og så videre, til den n-te likningen legger vi den andre, multiplisert med . Ligningssystemet etter slike transformasjoner vil ta formen

hvor og . Dermed er variabelen x 2 ekskludert fra alle ligninger, fra den tredje.

Deretter fortsetter vi med å eliminere den ukjente x 3, mens vi handler på samme måte med den delen av systemet som er merket på figuren

Så vi fortsetter den direkte progresjonen av Gauss-metoden til systemet tar formen

Fra dette øyeblikket begynner vi det motsatte av Gauss-metoden: vi beregner x n fra den siste ligningen som , ved å bruke den oppnådde verdien av x n finner vi x n-1 fra den nest siste ligningen, og så videre, vi finner x 1 fra den første ligningen .

Eksempel.

Løs system av lineære ligninger Gauss metode.

Løsning.

La oss ekskludere den ukjente variabelen x 1 fra den andre og tredje likningen i systemet. For å gjøre dette legger vi til begge sider av den andre og tredje ligningen de tilsvarende delene av den første ligningen, multiplisert med og med henholdsvis:

Nå eliminerer vi x 2 fra den tredje ligningen ved å legge til venstre og høyre side til venstre og høyre side av den andre ligningen, multiplisert med:

Dette fullfører det fremre slaget til Gauss-metoden; vi begynner slaget bakover.

Fra den siste ligningen til det resulterende ligningssystemet finner vi x 3:

Fra den andre ligningen får vi .

Fra den første ligningen finner vi den gjenværende ukjente variabelen og fullfører dermed det motsatte av Gauss-metoden.

Svar:

X 1 = 4, x 2 = 0, x 3 = -1.

Løse systemer av lineære algebraiske ligninger av generell form.

Generelt faller ikke antall ligninger i systemet p sammen med antall ukjente variabler n:

Slike SLAE-er har kanskje ingen løsninger, har en enkelt løsning eller har uendelig mange løsninger. Denne uttalelsen gjelder også for ligningssystemer hvis hovedmatrise er kvadratisk og entall.

Kronecker-Capelli teorem.

Før du finner en løsning på et system med lineære ligninger, er det nødvendig å etablere kompatibiliteten. Svaret på spørsmålet når SLAE er kompatibelt og når det er inkonsekvent er gitt av Kronecker-Capelli teorem:
For at et likningssystem med n ukjente (p kan være lik n) skal være konsistent, er det nødvendig og tilstrekkelig at rangeringen til systemets hovedmatris er lik rangeringen til den utvidede matrisen, dvs. , Rangering(A)=Rank(T).

La oss vurdere, som et eksempel, anvendelsen av Kronecker-Capelli-teoremet for å bestemme kompatibiliteten til et system med lineære ligninger.

Eksempel.

Finn ut om systemet med lineære ligninger har løsninger.

Løsning.

. La oss bruke metoden for å grense til mindreårige. Mindre av andre orden forskjellig fra null. La oss se på tredjeordens mindreårige som grenser til det:

Siden alle de grensende mindreårige av den tredje orden er lik null, er rangeringen til hovedmatrisen lik to.

I sin tur, rangeringen av den utvidede matrisen er lik tre, siden mindretallet er av tredje orden

forskjellig fra null.

Dermed, Rang(A), derfor, ved å bruke Kronecker-Capelli-setningen, kan vi konkludere med at det opprinnelige systemet med lineære ligninger er inkonsekvent.

Svar:

Systemet har ingen løsninger.

Så vi har lært å etablere inkonsistensen til et system ved å bruke Kronecker-Capelli-teoremet.

Men hvordan finne en løsning på en SLAE hvis kompatibiliteten er etablert?

For å gjøre dette trenger vi konseptet med en basismoll av en matrise og et teorem om rangeringen til en matrise.

Den moll av høyeste orden av matrisen A, forskjellig fra null, kalles grunnleggende.

Fra definisjonen av en basis minor følger det at rekkefølgen er lik rangeringen av matrisen. For en matrise A som ikke er null, kan det være flere basis moll; det er alltid en basis moll.

Tenk for eksempel på matrisen .

Alle tredjeordens mindreårige i denne matrisen er lik null, siden elementene i den tredje raden i denne matrisen er summen av de tilsvarende elementene i den første og andre raden.

Følgende andreordens mindreårige er grunnleggende, siden de ikke er null

Mindreårige er ikke grunnleggende, siden de er lik null.

Matriserangeringsteorem.

Hvis rangeringen av en matrise av orden p til n er lik r, blir alle rad- (og kolonne-)elementer i matrisen som ikke utgjør den valgte basis-moll lineært uttrykt i form av de korresponderende rad- (og kolonneelementene) som danner basis mindre.

Hva forteller matriserangeringssetningen oss?

Hvis vi i henhold til Kronecker-Capelli-teoremet har etablert kompatibiliteten til systemet, velger vi hvilken som helst basis-minor av hovedmatrisen til systemet (rekkefølgen er lik r), og ekskluderer fra systemet alle ligninger som gjør det ikke utgjør den valgte basis mindreårige. SLAE oppnådd på denne måten vil være ekvivalent med den opprinnelige, siden de forkastede ligningene fortsatt er overflødige (ifølge matriserangsetningen er de en lineær kombinasjon av de gjenværende ligningene).

Som et resultat, etter å ha forkastet unødvendige ligninger av systemet, er to tilfeller mulige.

Hvis antall ligninger r i det resulterende systemet er lik antallet ukjente variabler, vil det være definitivt og den eneste løsningen kan finnes ved Cramer-metoden, matrisemetoden eller Gauss-metoden.

Eksempel.

.

Løsning.

Rangering av hovedmatrisen til systemet er lik to, siden minor er av andre orden forskjellig fra null. Utvidet matriserangering er også lik to, siden den eneste tredje ordens moll er null

og andreordens moll som er vurdert ovenfor er forskjellig fra null. Basert på Kronecker-Capelli-teoremet kan vi hevde kompatibiliteten til det opprinnelige systemet med lineære ligninger, siden Rank(A)=Rank(T)=2.

Som basis mindre tar vi . Den er dannet av koeffisientene til den første og andre ligningen:


Den tredje ligningen til systemet deltar ikke i dannelsen av basisminor, så vi ekskluderer den fra systemet basert på teoremet om rangeringen av matrisen:


Dette er hvordan vi fikk et elementært system av lineære algebraiske ligninger. La oss løse det ved å bruke Cramers metode:


Svar:

x 1 = 1, x 2 = 2.

Hvis antall ligninger r i den resulterende SLAE mindre antall ukjente variabler n, så lar vi på venstre side av likningene vilkårene som danner basismoll, og vi overfører de resterende leddene til høyresiden av likningene i systemet med motsatt fortegn.

De ukjente variablene (r av dem) som er igjen på venstre side av ligningene kalles hoved-.

Ukjente variabler (det er n - r-stykker) som er på høyre side kalles gratis.

Nå tror vi at frie ukjente variabler kan ta vilkårlige verdier, mens de r viktigste ukjente variablene vil uttrykkes gjennom frie ukjente variabler på en unik måte. Uttrykket deres kan bli funnet ved å løse den resulterende SLAE ved å bruke Cramer-metoden, matrisemetoden eller Gauss-metoden.

La oss se på det med et eksempel.

Eksempel.

Løs et system med lineære algebraiske ligninger .

Løsning.

La oss finne rangeringen til hovedmatrisen til systemet ved å grense mindreårige. La oss ta en 1 1 = 1 som en ikke-null moll av første orden. La oss begynne å søke etter en moll som ikke er null av andre orden som grenser til denne moll:


Slik fant vi en moll som ikke er null av andre orden. La oss begynne å søke etter en moll som ikke er null av tredje orden:


Dermed er rangeringen av hovedmatrisen tre. Rangeringen til den utvidede matrisen er også lik tre, det vil si at systemet er konsistent.

Vi tar den funnet ikke-null moll av tredje orden som basis en.

For klarhets skyld viser vi elementene som danner basisminor:


Vi lar begrepene som er involvert i basis-moll på venstre side av systemligningene, og overfører resten med motsatte fortegn til høyre side:


La oss gi de frie ukjente variablene x 2 og x 5 vilkårlige verdier, det vil si at vi godtar , hvor er vilkårlige tall. I dette tilfellet vil SLAE ta formen


La oss løse det resulterende elementære systemet med lineære algebraiske ligninger ved å bruke Cramers metode:


Derfor,.

I svaret ditt, ikke glem å angi ledige ukjente variabler.

Svar:

Hvor er vilkårlige tall.

Oppsummer.

For å løse et system med generelle lineære algebraiske ligninger, bestemmer vi først dets kompatibilitet ved å bruke Kronecker-Capelli-teoremet. Hvis rangeringen til hovedmatrisen ikke er lik rangeringen til den utvidede matrisen, konkluderer vi med at systemet er inkompatibelt.

Hvis rangeringen til hovedmatrisen er lik rangeringen til den utvidede matrisen, velger vi en basis-minor og forkaster likningene til systemet som ikke deltar i dannelsen av den valgte basis-minor.

Hvis rekkefølgen på basisminoren er lik antall ukjente variabler, har SLAE en unik løsning, som kan finnes med en hvilken som helst metode kjent for oss.

Hvis rekkefølgen til basisminor er mindre enn antall ukjente variabler, lar vi på venstre side av systemligningene vilkårene med de viktigste ukjente variablene, overføre de resterende leddene til høyre side og gi vilkårlige verdier til de frie ukjente variablene. Fra det resulterende systemet med lineære ligninger finner vi de viktigste ukjente variablene ved å bruke Cramer-metoden, matrisemetoden eller Gauss-metoden.

Gauss-metode for å løse systemer av lineære algebraiske ligninger av generell form.

Gauss-metoden kan brukes til å løse systemer med lineære algebraiske ligninger av noe slag uten først å teste dem for konsistens. Prosessen med sekvensiell eliminering av ukjente variabler gjør det mulig å trekke en konklusjon om både kompatibiliteten og inkompatibiliteten til SLAE, og hvis en løsning finnes, gjør den det mulig å finne den.

Fra et beregningsmessig synspunkt er Gauss-metoden å foretrekke.

Se det Detaljert beskrivelse og analyserte eksempler i artikkelen Gauss-metoden for å løse systemer av lineære algebraiske ligninger av generell form.

Skrive en generell løsning på homogene og inhomogene lineære algebraiske systemer ved å bruke vektorer av det fundamentale løsningssystemet.

I denne delen skal vi snakke om samtidige homogene og inhomogene systemer av lineære algebraiske ligninger som har et uendelig antall løsninger.

La oss først ta for oss homogene systemer.

Grunnleggende system av løsninger homogent system av p lineære algebraiske ligninger med n ukjente variabler er en samling av (n – r) lineært uavhengige løsninger av dette systemet, hvor r er rekkefølgen til basis-moll av hovedmatrisen til systemet.

Hvis vi betegner lineært uavhengige løsninger av en homogen SLAE som X (1) , er X (2) , …, X (n-r) (X (1) , X (2) , …, X (n-r) søylematriser med dimensjon n med 1) , så er den generelle løsningen av dette homogene systemet representert som en lineær kombinasjon av vektorer av det grunnleggende løsningssystemet med vilkårlige konstante koeffisienter C 1, C 2, ..., C (n-r), det vil si .

Hva betyr begrepet generell løsning av et homogent system av lineære algebraiske ligninger (oroslau)?

Betydningen er enkel: formelen setter alt mulige løsninger den opprinnelige SLAE, med andre ord, ved å ta ethvert sett med verdier av vilkårlige konstanter C 1, C 2, ..., C (n-r), i henhold til formelen vil vi oppnå en av løsningene til den opprinnelige homogene SLAE.

Derfor, hvis vi finner et grunnleggende system av løsninger, kan vi definere alle løsninger av denne homogene SLAE som .

La oss vise prosessen med å konstruere et grunnleggende system av løsninger til en homogen SLAE.

Vi velger basis-moll for det opprinnelige systemet med lineære ligninger, ekskluderer alle andre ligninger fra systemet og overfører alle ledd som inneholder frie ukjente variabler til høyresiden av systemlikningene med motsatte fortegn. La oss gi gratis ukjente variable verdier 1,0,0,...,0 og beregne de viktigste ukjente ved å løse det resulterende elementære systemet med lineære ligninger på en hvilken som helst måte, for eksempel ved å bruke Cramer-metoden. Dette vil resultere i X (1) - den første løsningen av det grunnleggende systemet. Hvis vi gir de frie ukjente verdiene 0,1,0,0,...,0 og beregner de viktigste ukjente, får vi X (2) . Og så videre. Hvis vi tilordner verdiene 0.0,…,0.1 til de frie ukjente variablene og beregner de viktigste ukjente, får vi X (n-r) . På denne måten vil et grunnleggende system av løsninger til en homogen SLAE bli konstruert og dens generelle løsning kan skrives i formen .

For inhomogene systemer med lineære algebraiske ligninger, er den generelle løsningen representert i formen , hvor er den generelle løsningen av det tilsvarende homogene systemet, og er den spesielle løsningen av den opprinnelige inhomogene SLAE, som vi oppnår ved å gi de frie ukjente verdiene ​​0,0,...,0 og beregne verdiene til de viktigste ukjente.

La oss se på eksempler.

Eksempel.

Finn det grunnleggende løsningssystemet og den generelle løsningen av et homogent system av lineære algebraiske ligninger .

Løsning.

Rangeringen av hovedmatrisen til homogene systemer av lineære ligninger er alltid lik rangeringen til den utvidede matrisen. La oss finne rangeringen til hovedmatrisen ved å bruke metoden for å grense til mindreårige. Som en ikke-null moll av første orden tar vi element a 1 1 = 9 av hovedmatrisen til systemet. La oss finne den avgrensende moll som ikke er null av andre orden:

En mindreårig av andre orden, forskjellig fra null, er funnet. La oss gå gjennom de mindreårige av tredje orden som grenser til den på leting etter en som ikke er null:

Alle tredje-ordens grensende mindreårige er lik null, derfor er rangeringen til hovedmatrisen og den utvidede matrisen lik to. La oss ta . For klarhet, la oss legge merke til elementene i systemet som danner det:

Den tredje ligningen til den opprinnelige SLAE deltar ikke i dannelsen av basisminor, derfor kan den ekskluderes:

Vi lar begrepene som inneholder de viktigste ukjente på høyre side av ligningene, og overfører begrepene med frie ukjente til høyre side:

La oss konstruere et grunnleggende system av løsninger til det opprinnelige homogene systemet med lineære ligninger. Det grunnleggende løsningssystemet til denne SLAE består av to løsninger, siden den opprinnelige SLAE inneholder fire ukjente variabler, og rekkefølgen på dens basisminor er lik to. For å finne X (1), gir vi de frie ukjente variablene verdiene x 2 = 1, x 4 = 0, så finner vi de viktigste ukjente fra ligningssystemet
.

1. Substitusjonsmetode: fra en hvilken som helst likning i systemet uttrykker vi en ukjent gjennom en annen og erstatter den med den andre likningen i systemet.

Oppgave. Løs ligningssystemet:

Løsning. Fra den første ligningen i systemet uttrykker vi på gjennom X og erstatte det med den andre ligningen i systemet. La oss få systemet tilsvarende den originale.

Etter å ha brakt lignende vilkår, vil systemet ta formen:

Fra den andre ligningen finner vi:. Sette denne verdien inn i ligningen på = 2 - 2X, vi får på= 3. Derfor er løsningen på dette systemet et tallpar.

2. Algebraisk addisjonsmetode: Ved å legge til to likninger får du en likning med én variabel.

Oppgave. Løs systemligningen:

Løsning. Multipliserer begge sider av den andre ligningen med 2, får vi systemet tilsvarende den originale. Legger vi til de to likningene til dette systemet, kommer vi til systemet

Etter å ha brakt lignende vilkår, vil dette systemet ta formen: Fra den andre ligningen finner vi . Sett inn denne verdien i ligning 3 X + 4på= 5, får vi , hvor . Derfor er løsningen på dette systemet et tallpar.

3. Metode for å introdusere nye variabler: vi ser etter noen repeterende uttrykk i systemet, som vi vil betegne med nye variabler, og dermed forenkle utseendet til systemet.

Oppgave. Løs ligningssystemet:

Løsning. La oss skrive dette systemet annerledes:

La x + y = u, xy = v. Da får vi systemet

La oss løse det ved å bruke substitusjonsmetoden. Fra den første ligningen i systemet uttrykker vi u gjennom v og erstatte det med den andre ligningen i systemet. La oss få systemet de.

Fra den andre ligningen i systemet finner vi v 1 = 2, v 2 = 3.

Sett inn disse verdiene i ligningen u = 5 - v, vi får u 1 = 3,
u 2 = 2. Da har vi to systemer

Når vi løser det første systemet, får vi to tallpar (1; 2), (2; 1). Det andre systemet har ingen løsninger.

Øvelser for selvstendig arbeid

1. Løs ligningssystemer ved å bruke substitusjonsmetoden.

Leksjonens innhold

Lineære ligninger i to variabler

Et skolebarn har 200 rubler å spise lunsj på skolen. En kake koster 25 rubler, og en kopp kaffe koster 10 rubler. Hvor mange kaker og kopper kaffe kan du kjøpe for 200 rubler?

La oss angi antall kaker med x, og antall kopper kaffe gjennom y. Da vil prisen på kakene bli betegnet med uttrykket 25 x, og kostnaden for kopper kaffe i 10 y .

25x— pris x kaker
10y - pris y kopper kaffe

Det totale beløpet skal være 200 rubler. Da får vi en ligning med to variabler x Og y

25x+ 10y= 200

Hvor mange røtter har denne ligningen?

Alt avhenger av studentens appetitt. Hvis han kjøper 6 kaker og 5 kopper kaffe, vil røttene til ligningen være tallene 6 og 5.

Verdiparet 6 og 5 sies å være røttene til ligning 25 x+ 10y= 200. Skrevet som (6; 5), med det første tallet som verdien av variabelen x, og den andre - verdien av variabelen y .

6 og 5 er ikke de eneste røttene som reverserer ligning 25 x+ 10y= 200 til identitet. Hvis ønskelig, for de samme 200 rubler kan en student kjøpe 4 kaker og 10 kopper kaffe:

I dette tilfellet, røttene til ligning 25 x+ 10y= 200 er et verdipar (4; 10).

Dessuten kan et skolebarn kanskje ikke kjøpe kaffe i det hele tatt, men kjøpe kaker for hele 200 rubler. Deretter røttene til ligning 25 x+ 10y= 200 vil være verdiene 8 og 0

Eller omvendt, ikke kjøp kaker, men kjøp kaffe for hele 200 rubler. Deretter røttene til ligning 25 x+ 10y= 200 vil verdiene være 0 og 20

La oss prøve å liste opp alle mulige røtter til ligning 25 x+ 10y= 200. La oss være enige om at verdiene x Og y tilhører settet med heltall. Og la disse verdiene være større enn eller lik null:

x∈Z, y∈ Z;
x ≥ 0, y ≥ 0

Dette vil være praktisk for studenten selv. Det er mer praktisk å kjøpe hele kaker enn for eksempel flere hele kaker og en halv kake. Det er også mer praktisk å ta kaffe i hele kopper enn for eksempel flere hele kopper og en halv kopp.

Merk at for oddetall x det er umulig å oppnå likestilling under noen omstendigheter y. Så verdiene x følgende tall vil være 0, 2, 4, 6, 8. Og å vite x kan lett bestemmes y

Dermed mottok vi følgende verdipar (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Disse parene er løsninger eller røtter til ligning 25 x+ 10y= 200. De gjør denne ligningen til en identitet.

Formens ligning ax + by = c kalt lineær ligning med to variabler. Løsningen eller røttene til denne ligningen er et par verdier ( x; y), som gjør det til identitet.

Merk også at hvis en lineær ligning med to variabler skrives i skjemaet ax + b y = c , så sier de at det er skrevet inn kanonisk(normal) form.

Noen lineære ligninger i to variabler kan reduseres til kanonisk form.

For eksempel ligningen 2(16x+ 3y - 4) = 2(12 + 8x − y) kan bringes i tankene ax + by = c. La oss åpne parentesene på begge sider av denne ligningen og få 32x + 6y − 8 = 24 + 16x − 2y . Vi grupperer termer som inneholder ukjente på venstre side av ligningen, og termer fri for ukjente - til høyre. Så får vi 32x− 16x+ 6y+ 2y = 24 + 8 . Vi presenterer lignende termer på begge sider, vi får ligning 16 x+ 8y= 32. Denne ligningen er redusert til formen ax + by = c og er kanonisk.

Ligning 25 diskutert tidligere x+ 10y= 200 er også en lineær ligning med to variabler i kanonisk form. I denne ligningen parametrene en , b Og c er lik henholdsvis verdiene 25, 10 og 200.

Egentlig ligningen ax + by = c har utallige løsninger. Løse ligningen 25x+ 10y= 200, vi så etter røttene bare på settet med heltall. Som et resultat fikk vi flere verdipar som gjorde denne ligningen til en identitet. Men på settet med rasjonelle tall, ligning 25 x+ 10y= 200 vil ha uendelig mange løsninger.

For å få nye verdipar må du ta en vilkårlig verdi for x, så uttrykk y. La oss for eksempel ta for variabelen x verdi 7. Da får vi en likning med én variabel 25×7 + 10y= 200 der man kan uttrykke seg y

La x= 15. Så ligningen 25x+ 10y= 200 blir 25 × 15 + 10y= 200. Herfra finner vi det y = −17,5

La x= −3 . Så ligningen 25x+ 10y= 200 blir 25 × (−3) + 10y= 200. Herfra finner vi det y = −27,5

System av to lineære ligninger med to variabler

For ligningen ax + by = c du kan ta vilkårlige verdier så mange ganger du vil x og finne verdier for y. Sett hver for seg vil en slik ligning ha utallige løsninger.

Men det hender også at variablene x Og y ikke forbundet med én, men med to ligninger. I dette tilfellet danner de den såkalte system av lineære ligninger i to variabler. Et slikt ligningssystem kan ha ett verdipar (eller med andre ord: "én løsning").

Det kan også skje at systemet ikke har noen løsninger i det hele tatt. Et system med lineære ligninger kan ha utallige løsninger i sjeldne og eksepsjonelle tilfeller.

To lineære ligninger danner et system når verdiene x Og y gå inn i hver av disse ligningene.

La oss gå tilbake til den aller første ligningen 25 x+ 10y= 200 . Et av verdiparene for denne ligningen var paret (6; 5) . Dette er et tilfelle når du for 200 rubler kan kjøpe 6 kaker og 5 kopper kaffe.

La oss formulere oppgaven slik at paret (6; 5) blir den eneste løsningen for ligning 25 x+ 10y= 200. For å gjøre dette, la oss lage en annen ligning som vil koble det samme x kaker og y kopper kaffe.

La oss angi teksten til problemet som følger:

«Eleven kjøpte flere kaker og flere kopper kaffe for 200 rubler. En kake koster 25 rubler, og en kopp kaffe koster 10 rubler. Hvor mange kaker og kaffekopper kjøpte eleven dersom man vet at antall kaker er én enhet større enn antall kopper kaffe?

Vi har allerede den første ligningen. Dette er ligning 25 x+ 10y= 200. La oss nå lage en ligning for tilstanden "antall kaker er én enhet større enn antall kopper kaffe" .

Antall kaker er x, og antall kopper kaffe er y. Du kan skrive denne setningen ved å bruke ligningen x−y= 1. Denne ligningen vil bety at forskjellen mellom kaker og kaffe er 1.

x = y+ 1. Denne ligningen betyr at antall kaker er én mer enn antall kopper kaffe. Derfor, for å oppnå likhet, legges man til antall kopper kaffe. Dette kan lett forstås hvis vi bruker skalamodellen som vi vurderte når vi studerte de enkleste problemene:

Vi har to ligninger: 25 x+ 10y= 200 og x = y+ 1. Siden verdiene x Og y, nemlig 6 og 5 er inkludert i hver av disse ligningene, så danner de sammen et system. La oss skrive ned dette systemet. Hvis ligningene danner et system, er de innrammet av systemtegnet. Systemsymbolet er en krøllete klammeparentes:

La oss løse dette systemet. Dette vil tillate oss å se hvordan vi kommer frem til verdiene 6 og 5. Det er mange metoder for å løse slike systemer. La oss se på de mest populære av dem.

Substitusjonsmetode

Navnet på denne metoden taler for seg selv. Dens essens er å erstatte en ligning med en annen, etter å ha uttrykt en av variablene tidligere.

I vårt system trenger ingenting å uttrykkes. I den andre ligningen x = y+ 1 variabel x allerede uttrykt. Denne variabelen er lik uttrykket y+ 1. Deretter kan du erstatte dette uttrykket i den første ligningen i stedet for variabelen x

Etter å ha erstattet uttrykket y+ 1 i den første ligningen i stedet x, får vi ligningen 25(y+ 1) + 10y= 200 . Dette er en lineær ligning med én variabel. Denne ligningen er ganske enkel å løse:

Vi fant verdien av variabelen y. La oss nå erstatte denne verdien i en av ligningene og finne verdien x. For dette er det praktisk å bruke den andre ligningen x = y+ 1. La oss erstatte verdien i den y

Dette betyr at paret (6; 5) er en løsning på ligningssystemet, slik vi hadde tenkt. Vi sjekker og forsikrer oss om at paret (6; 5) tilfredsstiller systemet:

Eksempel 2

La oss erstatte den første ligningen x= 2 + y inn i den andre ligningen 3 x− 2y= 9. I den første ligningen er variabelen x lik uttrykket 2+ y. La oss erstatte dette uttrykket i den andre ligningen i stedet for x

La oss nå finne verdien x. For å gjøre dette, la oss erstatte verdien y inn i den første ligningen x= 2 + y

Dette betyr at løsningen på systemet er parverdien (5; 3)

Eksempel 3. Løs følgende ligningssystem ved å bruke substitusjonsmetoden:

Her, i motsetning til tidligere eksempler, er en av variablene ikke uttrykt eksplisitt.

For å erstatte en ligning med en annen, trenger du først .

Det er tilrådelig å uttrykke variabelen som har en koeffisient på én. Variabelen har en koeffisient på én x, som er inneholdt i den første ligningen x+ 2y= 11. La oss uttrykke denne variabelen.

Etter variabelt uttrykk x, vil systemet vårt ha følgende form:

La oss nå erstatte den første ligningen med den andre og finne verdien y

La oss erstatte y x

Dette betyr at løsningen på systemet er et par verdier (3; 4)

Du kan selvfølgelig også uttrykke en variabel y. Dette vil ikke endre røttene. Men hvis du uttrykker y, Resultatet er ikke en veldig enkel ligning, som vil ta lengre tid å løse. Det vil se slik ut:

Det ser vi i i dette eksempletå uttrykke x mye mer praktisk enn å uttrykke y .

Eksempel 4. Løs følgende ligningssystem ved å bruke substitusjonsmetoden:

La oss uttrykke i den første ligningen x. Da vil systemet ta formen:

y

La oss erstatte y inn i den første ligningen og finn x. Du kan bruke den opprinnelige ligningen 7 x+ 9y= 8, eller bruk ligningen der variabelen er uttrykt x. Vi vil bruke denne ligningen fordi den er praktisk:

Dette betyr at løsningen på systemet er et par verdier (5; −3)

Tilleggsmetode

Addisjonsmetoden består i å legge til likningene som inngår i systemet termin for ledd. Dette tillegget resulterer i en ny ligning med én variabel. Og å løse en slik ligning er ganske enkelt.

La oss løse følgende ligningssystem:

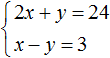
La oss legge til venstre side av den første ligningen med venstre side av den andre ligningen. Og høyre side av den første ligningen med høyre side av den andre ligningen. Vi får følgende likestilling:

La oss se på lignende termer:

Som et resultat fikk vi den enkleste ligningen 3 x= 27 hvis rot er 9. Å kjenne verdien x du kan finne verdien y. La oss erstatte verdien x inn i den andre ligningen x−y= 3. Vi får 9 − y= 3. Herfra y= 6 .

Dette betyr at løsningen på systemet er et par verdier (9; 6)

Eksempel 2

La oss legge til venstre side av den første ligningen med venstre side av den andre ligningen. Og høyre side av den første ligningen med høyre side av den andre ligningen. I den resulterende likheten presenterer vi lignende termer:

Som et resultat fikk vi den enkleste ligningen 5 x= 20, hvis rot er 4. Å kjenne verdien x du kan finne verdien y. La oss erstatte verdien x inn i den første ligningen 2 x+y= 11. La oss få 8+ y= 11. Herfra y= 3 .

Dette betyr at løsningen på systemet er et par verdier (4;3)

Tilsetningsprosessen er ikke beskrevet i detalj. Det må gjøres mentalt. Ved addering må begge ligningene reduseres til kanonisk form. Det vil si forresten ac + by = c .

Fra de vurderte eksemplene er det klart at hovedhensikten med å legge til ligninger er å bli kvitt en av variablene. Men det er ikke alltid mulig å umiddelbart løse et likningssystem ved hjelp av addisjonsmetoden. Som oftest bringes systemet først til en form der ligningene som inngår i dette systemet kan legges til.

For eksempel systemet kan løses umiddelbart ved tilsetning. Når du legger til begge ligningene, vil begrepene y Og −y vil forsvinne fordi summen deres er null. Som et resultat dannes den enkleste ligningen 11 x= 22, hvis rot er 2. Det vil da være mulig å bestemme y lik 5.

Og ligningssystemet Addisjonsmetoden kan ikke løses umiddelbart, siden dette ikke vil føre til at en av variablene forsvinner. Addisjon vil resultere i ligning 8 x+ y= 28, som har et uendelig antall løsninger.

Hvis begge sider av ligningen multipliseres eller divideres med samme tall, ikke lik null, får du en ligning tilsvarende den gitte. Denne regelen gjelder også for et system av lineære ligninger med to variabler. En av ligningene (eller begge ligningene) kan multipliseres med et hvilket som helst tall. Resultatet vil være et ekvivalent system, hvis røtter vil falle sammen med det forrige.

La oss gå tilbake til det aller første systemet, som beskrev hvor mange kaker og kaffekopper et skolebarn kjøpte. Løsningen på dette systemet var et par verdier (6; 5).

La oss multiplisere begge ligningene som er inkludert i dette systemet med noen tall. La oss si at vi multipliserer den første ligningen med 2, og den andre med 3

Som et resultat fikk vi et system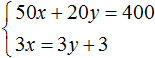
Løsningen på dette systemet er fortsatt verdiparet (6; 5)

Dette betyr at likningene som inngår i systemet kan reduseres til en form som egner seg for å anvende addisjonsmetoden.

La oss gå tilbake til systemet , som vi ikke kunne løse ved hjelp av addisjonsmetoden.

Multipliser den første ligningen med 6, og den andre med −2

Da får vi følgende system:

La oss legge sammen ligningene som er inkludert i dette systemet. Legge til komponenter 12 x og -12 x vil resultere i 0, tillegg 18 y og 4 y vil gi 22 y, og å legge til 108 og −20 gir 88. Da får vi ligning 22 y= 88, herfra y = 4 .

Hvis det først er vanskelig å legge til ligninger i hodet ditt, kan du skrive ned hvordan venstre side av den første ligningen går sammen med venstre side av den andre ligningen, og høyre side av første ligning med høyre side av ligningen. andre ligning:

Å vite at verdien av variabelen y lik 4, kan du finne verdien x. La oss erstatte y inn i en av ligningene, for eksempel inn i den første ligningen 2 x+ 3y= 18. Da får vi en ligning med én variabel 2 x+ 12 = 18. La oss flytte 12 til høyre side, endre tegnet, vi får 2 x= 6, herfra x = 3 .

Eksempel 4. Løs følgende ligningssystem ved å bruke addisjonsmetoden:

La oss multiplisere den andre ligningen med −1. Da vil systemet ha følgende form:

La oss legge til begge ligningene. Legge til komponenter x Og −x vil resultere i 0, tillegg 5 y og 3 y vil gi 8 y, og å legge til 7 og 1 gir 8. Resultatet er ligning 8 y= 8 hvis rot er 1. Å vite at verdien y lik 1, kan du finne verdien x .

La oss erstatte y inn i den første ligningen, får vi x+ 5 = 7, derav x= 2

Eksempel 5. Løs følgende ligningssystem ved å bruke addisjonsmetoden:

Det er ønskelig at termer som inneholder de samme variablene er plassert under hverandre. Derfor, i den andre ligningen, vilkårene 5 y og −2 x La oss bytte plass. Som et resultat vil systemet ta formen:

La oss multiplisere den andre ligningen med 3. Da vil systemet ha formen:

La oss nå legge til begge ligningene. Som et resultat av addisjon får vi ligning 8 y= 16, hvis rot er 2.

La oss erstatte y inn i den første ligningen får vi 6 x− 14 = 40. La oss flytte begrepet −14 til høyre, endre tegnet og få 6 x= 54. Herfra x= 9.

Eksempel 6. Løs følgende ligningssystem ved å bruke addisjonsmetoden:

La oss bli kvitt brøker. Multipliser den første ligningen med 36, og den andre med 12

I det resulterende systemet den første ligningen kan multipliseres med −5, og den andre med 8

La oss legge sammen ligningene i det resulterende systemet. Da får vi den enkleste ligningen −13 y= −156 . Herfra y= 12. La oss erstatte y inn i den første ligningen og finn x

Eksempel 7. Løs følgende ligningssystem ved å bruke addisjonsmetoden:

La oss bringe begge likningene til normal form. Her er det praktisk å bruke proporsjonsregelen i begge ligningene. Hvis høyresiden i den første ligningen er representert som , og høyresiden av den andre ligningen som , vil systemet ha formen:

Vi har en andel. La oss multiplisere dens ekstreme og mellomste termer. Da vil systemet ta formen:

La oss multiplisere den første ligningen med −3, og åpne parentesene i den andre:

La oss nå legge til begge ligningene. Som et resultat av å legge til disse ligningene får vi en likhet med null på begge sider:

Det viser seg at systemet har utallige løsninger.

Men vi kan ikke bare ta vilkårlige verdier fra himmelen for x Og y. Vi kan spesifisere en av verdiene, og den andre vil bli bestemt avhengig av verdien vi spesifiserer. La for eksempel x= 2 . La oss erstatte denne verdien i systemet:

Som et resultat av å løse en av ligningene vil verdien for y, som vil tilfredsstille begge ligningene:

Det resulterende verdiparet (2; −2) vil tilfredsstille systemet:

La oss finne et annet verdipar. La x= 4. La oss erstatte denne verdien i systemet:

Du kan se på øyet at verdien y er lik null. Da får vi et verdipar (4; 0) som tilfredsstiller systemet vårt:

Eksempel 8. Løs følgende ligningssystem ved å bruke addisjonsmetoden:

Multipliser den første ligningen med 6 og den andre med 12

La oss skrive om det som er igjen:

La oss multiplisere den første ligningen med −1. Da vil systemet ta formen:

La oss nå legge til begge ligningene. Som et resultat av addisjon dannes ligning 6 b= 48, hvis rot er 8. Erstatter b inn i den første ligningen og finn en

System av lineære ligninger med tre variabler

En lineær ligning med tre variabler inkluderer tre variabler med koeffisienter, samt et avskjæringsledd. I kanonisk form kan det skrives som følger:

ax + by + cz = d

Denne ligningen har utallige løsninger. Gir to variabler forskjellige betydninger, kan du finne en tredje verdi. Løsningen i dette tilfellet er en trippel av verdier ( x; y; z) som gjør ligningen til en identitet.

Hvis variablene x, y, z er forbundet med tre ligninger, så dannes et system med tre lineære ligninger med tre variabler. For å løse et slikt system kan du bruke de samme metodene som gjelder for lineære ligninger med to variabler: substitusjonsmetoden og addisjonsmetoden.

Eksempel 1. Løs følgende ligningssystem ved å bruke substitusjonsmetoden:

La oss uttrykke i den tredje ligningen x. Da vil systemet ta formen:

La oss nå gjøre erstatningen. Variabel x er lik uttrykket 3 − 2y − 2z . La oss erstatte dette uttrykket i den første og andre ligningen:

La oss åpne parentesene i begge ligningene og presentere lignende termer:

Vi har kommet til et system av lineære ligninger med to variabler. I dette tilfellet er det praktisk å bruke tilleggsmetoden. Som et resultat, variabelen y vil forsvinne og vi kan finne verdien av variabelen z

La oss nå finne verdien y. For å gjøre dette er det praktisk å bruke ligningen − y+ z= 4. Bytt inn verdien i den z

La oss nå finne verdien x. For å gjøre dette er det praktisk å bruke ligningen x= 3 − 2y − 2z . La oss erstatte verdiene i den y Og z

Dermed er trippelen av verdier (3; −2; 2) en løsning på systemet vårt. Ved å sjekke sikrer vi at disse verdiene tilfredsstiller systemet:

Eksempel 2. Løs systemet ved å bruke addisjonsmetoden

La oss legge til den første ligningen med den andre, multiplisert med −2.

Hvis den andre ligningen multipliseres med −2, tar den formen −6x+ 6y - 4z = −4 . La oss nå legge det til den første ligningen:

Vi ser at som et resultat av elementære transformasjoner ble verdien av variabelen bestemt x. Det er lik en.

La oss gå tilbake til hovedsystemet. La oss legge til den andre ligningen med den tredje, multiplisert med −1. Hvis den tredje ligningen multipliseres med −1, tar den formen −4x + 5y − 2z = −1 . La oss nå legge det til den andre ligningen:

Vi har ligningen x− 2y= −1 . La oss erstatte verdien i den x som vi fant tidligere. Så kan vi bestemme verdien y

Nå vet vi betydningen x Og y. Dette lar deg bestemme verdien z. La oss bruke en av ligningene som er inkludert i systemet:

Dermed er trippelen av verdier (1; 1; 1) løsningen på systemet vårt. Ved å sjekke sikrer vi at disse verdiene tilfredsstiller systemet:

Problemer med å komponere systemer av lineære ligninger

Oppgaven med å komponere ligningssystemer løses ved å legge inn flere variabler. Deretter kompileres ligninger basert på betingelsene for problemet. Fra de kompilerte ligningene danner de et system og løser det. Etter å ha løst systemet, er det nødvendig å sjekke om løsningen tilfredsstiller betingelsene for problemet.

Oppgave 1. En Volga-bil kjørte ut av byen til kollektivgården. Hun kom tilbake langs en annen vei, som var 5 km kortere enn den første. Totalt kjørte bilen 35 km tur/retur. Hvor mange kilometer er lengden på hver vei?

Løsning

La x— lengden på den første veien, y- lengden på den andre. Hvis bilen kjørte 35 km tur/retur, kan den første ligningen skrives som x+ y= 35. Denne ligningen beskriver summen av lengdene på begge veiene.

Det sies at bilen kom tilbake langs en vei som var 5 km kortere enn den første. Da kan den andre ligningen skrives som x− y= 5. Denne ligningen viser at forskjellen mellom veilengdene er 5 km.

Eller den andre ligningen kan skrives som x= y+ 5. Vi vil bruke denne ligningen.

Fordi variablene x Og y i begge ligningene angir det samme tallet, så kan vi danne et system fra dem:

La oss løse dette systemet ved å bruke noen av de tidligere studerte metodene. I dette tilfellet er det praktisk å bruke substitusjonsmetoden, siden variabelen i den andre ligningen x allerede uttrykt.

Bytt ut den andre ligningen med den første og finn y

La oss erstatte den funnet verdien y i den andre ligningen x= y+ 5 så finner vi x

Lengden på den første veien ble utpekt gjennom variabelen x. Nå har vi funnet meningen. Variabel x er lik 20. Dette betyr at lengden på den første veien er 20 km.

Og lengden på den andre veien ble angitt med y. Verdien av denne variabelen er 15. Dette betyr at lengden på den andre veien er 15 km.

La oss sjekke. Først, la oss sørge for at systemet er løst riktig:

La oss nå sjekke om løsningen (20; 15) tilfredsstiller betingelsene for problemet.

Det ble sagt at bilen kjørte totalt 35 km tur/retur. Vi legger til lengdene på begge veiene og sørger for at løsningen (20; 15) tilfredsstiller denne tilstanden: 20 km + 15 km = 35 km

Følgende tilstand: bilen kom tilbake langs en annen vei, som var 5 km kortere enn den første . Vi ser at løsningen (20; 15) også tilfredsstiller denne betingelsen, siden 15 km er kortere enn 20 km ganger 5 km: 20 km − 15 km = 5 km

Når man setter sammen et system, er det viktig at variablene representerer de samme tallene i alle ligninger som inngår i dette systemet.

Så vårt system inneholder to ligninger. Disse ligningene inneholder igjen variabler x Og y, som representerer de samme tallene i begge ligningene, nemlig veilengder på 20 km og 15 km.

Oppgave 2. Eik og furusviller ble lastet på plattformen, totalt 300 sviller. Det er kjent at alle eikesviller veide 1 tonn mindre enn alle furusviller. Bestem hvor mange eike- og furusviller det var separat, hvis hver eikesville veide 46 kg, og hver furusville 28 kg.

Løsning

La x eik og y furusviller ble lastet på plattformen. Hvis det var 300 sviller totalt, kan den første ligningen skrives som x+y = 300 .

Alle eikesviller veide 46 x kg, og furuene veide 28 y kg. Siden eikesviller veide 1 tonn mindre enn furusviller, kan den andre ligningen skrives som 28y - 46x= 1000 . Denne ligningen viser at forskjellen i masse mellom eik og furusviller er 1000 kg.

Tonn ble omregnet til kilo siden massen av eik- og furusviller ble målt i kilo.

Som et resultat får vi to ligninger som danner systemet

La oss løse dette systemet. La oss uttrykke i den første ligningen x. Da vil systemet ta formen:

Bytt ut den første ligningen med den andre og finn y

La oss erstatte y inn i ligningen x= 300 − y og finne ut hva det er x

Det betyr at 100 eik og 200 furusviller ble lastet på plattformen.

La oss sjekke om løsningen (100; 200) tilfredsstiller betingelsene for problemet. Først, la oss sørge for at systemet er løst riktig:

Det ble sagt at det var 300 sviller totalt. Vi summerer antallet eike- og furusviller og forsikrer oss om at løsningen (100; 200) tilfredsstiller denne betingelsen: 100 + 200 = 300.

Følgende tilstand: alle eikesviller veide 1 tonn mindre enn alle furusviller . Vi ser at løsningen (100; 200) også tilfredsstiller denne betingelsen, siden 46 × 100 kg eikesviller er lettere enn 28 × 200 kg furusviller: 5600 kg − 4600 kg = 1000 kg.

Oppgave 3. Vi tok tre stykker kobber-nikkel-legering i vektforhold på 2: 1, 3: 1 og 5: 1. Et stykke som veide 12 kg ble smeltet fra dem med et forhold mellom kobber og nikkelinnhold på 4:1. Finn massen til hvert originalstykke hvis massen til den første er to ganger massen til den andre.